
Методика решения задач по оптике для студентов инженерных специальностей
.pdf
k1 = 1,
k2 = 2,
х= 60 мм =
=6 10-2 м.
λ– ?
Длины отрезков х1 и х2 найдем из решений соответствующих прямоугольных треугольников:
(1) x1 = Stgϕ1,
(2) x2 = Stgϕ2.
Ввиду малости углов дифракции спектров первого и второго порядков справедливо соотношение sinϕ = tgϕ . Тогда уравнения (1) и
(2) можно записать в ином виде: (3) x1 = S sinϕ1,
(4) x2 = S sinϕ2.
Разница между величинами х1 и х2, очевидно, равна х (см. рис.).
Условие главных дифракционных максимумов для спектров 1-го и 2-го порядков соответственно (см. формулу 2.11 в § 3.2):
(5) d sinϕ1 = k1λ, (6) d sinϕ2 = k2λ,
где d = L/N - период дифракционной решетки.
2*. |
|
|
|
белый |
|
|
|
свет |
|
D |
.C |
|
|
P |
M |
|
N |
|
|
|
ϕ1 |
|
|
|
S |
ϕ2 |
|
|
|
экран |
O |
|
A |
B |
|
k=0 |
x1 |
k=1 |
k=2 |
|
|
|
x |
|
|
|
|
x2 |
|
4*. Составим полную систему уравнений для нахождения искомой величины λ , обобщив все приведенные выше рассуждения:
- 60 -

(3) x1 = S sinϕ1,(4) x2 = S sinϕ2 .(5) d sinϕ1 = k1λ,(6) d sinϕ2 = k2λ,
(7) x = x2 − x1,
(8) d = L N .
N .
Система шести уравнений (3) – (8) замкнута, так как содержит шесть неизвестных величин: x1, x2 , ϕ1, ϕ2 , d, λ.
5*. Решим систему уравнений (3) – (8) относительно λ.
Подставив (3) и (4) в (7) и (8) в (5) и (6), получим систему трех уравнений с тремя неизвестными величинами:
|
x = S(sinϕ2 − sinϕ1 ), |
|||||||
(9) |
||||||||
|
Lsinϕ1 |
|
|
|
||||
(10) |
|
= k1λ, |
||||||
|
|
|||||||
|
N |
|
|
|
|
|||
(11) |
|
Lsinϕ2 |
|
= k2λ. |
||||
|
|
|
|
|||||
|
N |
|
|
|
|
|||
Вычитая из (11) уравнение (10), с учетом (9) получим |
||||||||
искомую величину λ: |
|
|
|
|
xL |
|||
(12) |
|
λ = |
|
|
|
|||
|
|
|
|
|
. |
|||
|
(k |
2 |
|
− k )SN |
||||
|
|
|
|
1 |
|
|||
6*. Проверка размерности полученной величины α :
[λ]= ммм = м.
7*. Анализ решения. Полученная формула (12) позволяет вычислить искомую длину света, но вовсе не отражает зависимость длины волны от величин, стоящих в правой части формулы (12). Между тем формула (12) имеет приближенный характер и ограниченное применение до тех пор, пока угол ϕ мал
(до 10 …12º – 0,17 … 0,21 рад).
8*. Вычислим величину λ:
λ = 6 10−2 8 10−3 = 4,8 10-7 (м)= 480(нм). 1 1 103
- 61 -

9*. Ответ: λ = |
|
|
xL |
4,8 10−7 м = 480 нм. |
(k |
2 |
− k )SN |
||
|
|
1 |
|
***************
Задача 13 |
|
|
(νm ,T ), |
|
Вывести правило |
смещения Вина |
в координатах |
где |
|
νm − частота, |
соответствующая |
максимуму излучательной |
||
способности абсолютно черного |
тела ε(ν ,T ), |
T − |
его |
|
абсолютная температура.
1*.
Дано:
ε(ν ,T )
________
νm =
=f (T )−?
3*. |
|
Решение. |
|
Анализ |
задачи. |
Зависимость |
излучательной способности абсолютно черного тела ε(λ,T ) от длины волны λ подробно
исследована в [1], включая вывод правила смещения Вина в координатах (λm ,T ):
(1)λm = b T ,
T ,
где λm − длина волны, соответствующая
максимуму излучательной способности такого тела,
b − постоянная Вина,
T − термодинамическая температура.
Там же рассмотрены физические причины, не допускающие применения связи длины волны и частоты применительно к вакууму (с =νλ) тогда,
когда речь идет об аналогичных физических величинах, соответствующих максимуму излучательной способности абсолютно черного тела (с ≠νmλm ).
Между тем установить связь между частотой, соответствующей максимуму излучения, и абсолютной температурой абсолютно черного тела, очевидно, можно, пройдя тот же путь, приведший к правилу смещения Вина в координатах (λm ,T ). Таким образом, для
отыскания искомой зависимости необходимо найти частоту νm , соответствующую максимуму
излучения εm (νm ,T ). Следовательно, в качество первого шага следует продифференцировать
- 62 -

функцию ε(ν,T ) по частоте ν и приравнять
результат нулю. Затем решить полученное уравнение уже относительно νm . В процессе
решения будет найдена не только искомая зависимость, но и получен коэффициент Вина b′, отвечающий правилу смещения Вина в координатах (νm ,T ).
4*. Составим полную систему уравнений для нахождения искомой зависимости. С этой целью вспомним формулу Планка в координатах (ν,T ):
(2) |
ε(ν,T ) = |
2πν 2 |
|
|
hν |
|
. |
|
c2 |
|
hν |
|
|||||
|
|
|
|
|
||||
|
|
|
e kT −1 |
|
||||
|
|
|
|
|
||||
Вформуле (1) неизвестными являются лишь переменные ν и
Т. Остальные величины представляют собой константы (π ) и универсальные физические постоянные (h, c, k ). Таким образом,
полная система состоит из двух уравнений:
dε(ν ,T ) = 0, dν
ν =νm .
Система двух уравнений (3) – (4) замкнута, так как содержит три неизвестных величины: ν, νm , T (искомая зависимость
содержит сразу две переменных).
|
5*. |
Решим систему |
|
уравнений |
|
|
(3) |
– (4), получив |
||||||||||||||||||||||||||
зависимость νm = f (T ). Находим производную, заменяя ν наνm : |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
6πhν |
2 |
hν |
|
|
|
2πhν |
3 |
|
h |
|
|
hν |
|
|
|
|
|
|
|
|
hν |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πhν |
2 |
e kT |
|
|
||||||||||
|
|
|
|
|
|
|
|
e kT |
−1 − |
|
|
|
|
|
|
e kT |
|
|
|
|
|
|
||||||||||||
|
dε(ν ,T ) |
|
|
c |
2 |
|
|
c |
2 |
|
kT |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
||||||||||||||||
(5) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||||||||
|
dν |
|
|
|
|
|
|
|
hν |
|
2 |
|
|
|
|
|
|
|
|
hν |
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
e |
kT |
− |
1 |
|
|
|
|
|
|
|
|
|
e |
kT |
|
−1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- 63 -

|
|
|
|
|
|
|
|
|
|
|
|
|
2πhν |
2 |
|
|
hνm |
|
|
hν |
|
|
hνm |
|
|||
|
|
|
|
|
|
6πhν |
2 |
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
3e kT − 3 |
− |
e kT |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
hν |
|
|
|
|
|
|
c2 |
|
kT |
|
|||||||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0. |
|||||
3 |
− |
|
|
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
kT |
|
hν |
|
|
|
|
|
|
hνm |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
e kT |
1 |
|
|
|
|
|
e kT |
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решим полученное уравнение. Заметим, что νm ≠ 0, так как в данном случае знаменатель обращается в ноль. Если обозначить
х = hkTνm , то получим:
(6)3ex −3 − xex = 0.
Так как уравнение трансцендентное, решим его графически.
Прежде заметим, что размерность величины |
[х]= |
Дж с К |
=1. |
|
|
с Дж К |
|
Размерность каждого слагаемого уравнения (5) так же равняется единице ( х – безразмерная величина, показатель степени – безразмерная величина).
Представим уравнение (5) как два уравнения (систему):
y = xex +3,
xy = 3e .
Построим кривые, соответствующие уравнениям (7) в одной декартовой системе координат (см. рис. ниже). Единственным устраивающим нас решением является х ≈ 2,82 ( х ≈ 0 не является решением, так как обращает в ноль знаменатель уравнения (4)). Возвращаясь к первоначальным переменным, имеем:
(8) 2,82 = |
hνm |
, νm = |
2,82k |
T = |
2,82 1,38 10-23 |
T = 5,9 1010 |
T. |
|
h |
6,63 10-34 |
|||||
|
kT |
|
|
|
|||
Таким образом, b′ = 5,9 1010 (c-1 K-1).
Решение уравнения xex-3ex +3=0 графическим способом
- 64 -

Y65 |
|
y=x*ex +3 |
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
. |
|
|
|
50 |
|
|
|
|
|
|
45 |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
35 |
|
|
|
y=3*ex |
|
|
30 |
2.6 |
2.7 |
2.8 |
2.9 |
3 |
X |
2.5 |
6*. Размерность константы b′ легко определяется непосредственно из формулы
(8): |
[ν ] |
1 |
|
||
[b′]= |
|
||||
m |
|
= |
|
. |
|
[T ] |
c K |
||||
7*. Анализ решения.
Помножив левые и правые части формул Вина (1) и (8) (правила смещения соответственно в координатах
(λm ,T ) и (ν,T )), получим:
νmλm = b′b = 2,9 10−3 5,9 1010 ≈1,7 108 < 3 108 = c.
Справедливость полученного результата хорошо иллюстрируют графики зависимости излучательной способности соответственно от длины волны (см. график ниже, слева) и частоты (см.
график выше, справа). Очевидно, произведение νmλm ,
как следует из анализа графиков, меньше скорости света с, так как на правом графике максимумы функции ε(ν,T ) не «дотягивают» до
видимой области, в которой
- 65 -

лежат максимумы функции ε(λ,T ) на левом графике.
8*. Вычисление постоянной Вина b′ проведено в разделе 5* решения.
* νm = b′T ,
9 . Ответ:
b′ ≈ 5,9 1010 c-1 K-1.
***************
Задача 14
Нормированная сферически симметричная волновая функция, описывающая 1s-состояние электрона в атоме водорода, имеет
вид ψ(r) = 1 |
e -r a , где r − расстояние электрона от ядра, |
πа3 |
|
а = 0,53 10−10 м−первый боровский радиус. Определить среднюю потенциальную энергию U электрона в поле ядра.
Внимание! Следует различать заряд электрона e и показательную функцию с основанием e.
1*. Дано:
ψ(r) = 1 |
e -r a , |
πа3 |
|
а = 0,53 10−10 м,
e= 1,6 10−19 Кл,
ε0 = 8,85 10−12 Ф м.
м.
U – ?
Решение.
3*. Анализ задачи. В квантовой механике среднее значение какой-либо физической величины К, характеризующий объект, находящийся в состоянии, описываемом волновой функцией ψ , вычисляется через тройной
интеграл, под знаком которого в обязательном порядке располагается волновая ψ - функция, помноженная на
комплексно сопряженную с ней функцию и на физическую величину, среднее значение которой требуется определить:
К = ∫∫∫ Кψ
 2dV = ∫∫∫ Кψ
2dV = ∫∫∫ Кψ
 2dxdydz .
2dxdydz .
V V
Величина K в данном случае есть потенциальная энергия U электрона, обладающего зарядом e и находящегося на расстоянии r от ядра:
- 66 -
|
|
|
|
|
|
|
U = − |
e2 |
|
, |
|
|
|
|
|
|
|
|
4πε0r |
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
где ε0 − электрическая постоянная. |
|
||||
|
|
|
|
|
|
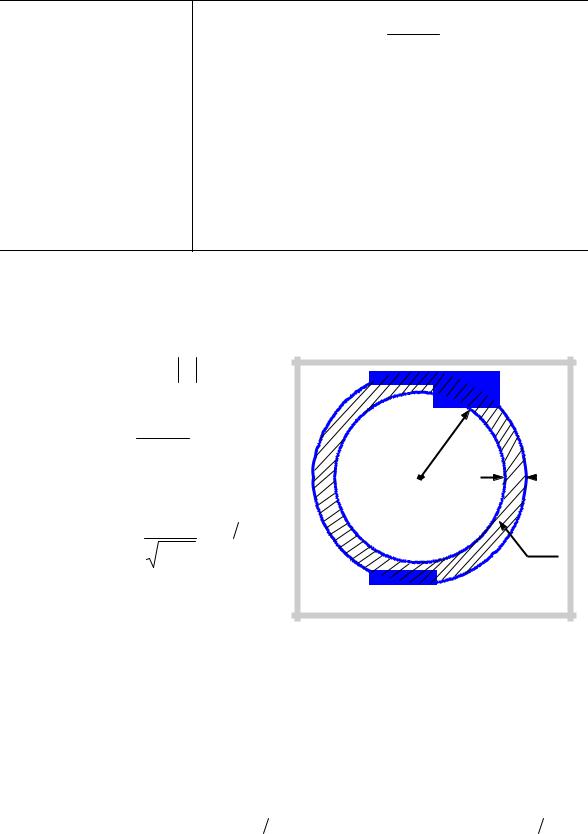
Кроме |
того, элемент |
объема dV |
в |
||
|
|
|
|
|
|
случае |
сферически |
|
симметричной |
||
|
|
|
|
|
|
волновой |
функции |
ψ |
|
представляется |
|
|
|
|
|
|
|
весьма просто с использованием одной |
|||||
|
|
|
|
|
|
переменной вместо трех (см.рис. ниже): |
|
||||
|
|
|
|
|
|
|
dV = 4πr2dr . |
|
|||
4*. Составим полную систему уравнений для нахождения |
|||||||||||
искомой величины U , обобщив все приведенные выше |
|||||||||||
рассуждения: |
|
|
|
|
|
|
|
|
|
|
|
(1) |
U = ∫∫∫Uψ 2dV , |
|
|
|
|
|
|||||
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
||
|
U = − |
|
, |
|
|
|
r |
|
|
||
(2) |
4πε0r |
|
|
|
|
|
|
||||
|
|
|
|
|
o |
|
dr |
|
|||
|
dV = 4πr |
2 |
dr, |
|
|
|
|
|
|||
(3) |
|
|
|
ядро |
|
||||||
|
|
|
1 |
|
e -r a , |
|
|
|
|
|
|
(4) |
ψ(r) = |
|
|
|
|
dV |
|
||||
|
|
πа3 |
|
|
|
|
|
|
|
||
(5) |
0 ≤ r < ∞. |
|
|
|
|
Плоскостное сечение |
|
||||
|
|
|
|
|
|
|
элемента |
объема dV |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Система пяти уравнений (1) – (5) замкнута, так как |
|||||||||||
содержит пять неизвестных величин: U , U , ψ , V , r . |
|
||||||||||
5*. Решим систему уравнений (1) – (5) относительно U .
Подставляя (2), (3), (4), (5) в (1), имеем:
∞ |
|
e2 |
1 |
|
|
−2r a |
|
2 |
|
e2 |
4 |
∞ |
−2r a |
|
||||
(6) U = ∫ |
|
− |
|
|
|
|
e |
4πr |
dr = − |
|
|
|
|
∫re |
dr = |
|||
|
|
|
πa |
3 |
|
|
|
|
3 |
|
||||||||
0 |
|
|
4πε0r |
|
|
|
|
|
|
4πε0 a |
|
0 |
|
|
||||
- 67 -

|
e2 |
|
4 |
|
|
a |
∞ |
|
= − |
|
|
|
|
− |
|
|
∫rde-2r a = (интеграл вычисляем по частям)= |
4πε0 |
a3 |
|
||||||
|
|
|
|
2 |
0 |
|||
|
e2 |
|
|
∞ |
∞ |
|
|
e |
2 |
|
a |
|
e2 |
|||
|
|
|
|
|
||||||||||||
= |
|
re-2r a |
|
|
− ∫e-2r adr |
= |
|
|
0 |
− |
|
|
= − |
|
. |
|
|
|
|
|
|
|
|
||||||||||
|
2a2πε0 |
|
0 |
0 |
|
|
2a2πε0 |
|
2 |
|
4aπε0 |
|||||
|
|
|
|
|
||||||||||||
6*. Проверка размерности (единицы измерения) полученной
величины |
U (воспользуемся приложением №4): |
|
|
||||||
[U ]= |
|
Кл2 |
= |
Кл2 |
= (А2 с2 ) м2 кг = |
м2 кг |
= Дж. |
||
м |
Ф м |
Ф |
|
||||||
7*. |
|
|
А2 с4 |
с2 |
|
||||
Анализ |
решения. |
Полученная формула |
(6) имеет |
||||||
отрицательный знак, что полностью согласуется с зонной теорией твердого тела. Значение же средней потенциальной энергии электрона в поле ядра совпадает с классическими представлениями о потенциальной энергии заряженной частицы, находящейся в кулоновском поле ядра (см. раздел физики «Электричество и магнетизм»). Этим, пожалуй, и ограничиваются совпадения в поведении электрона в поле ядра с классической заряженной частицей, так как в рассматриваемом случае нет возможности даже говорить о траектории электрона в привычном смысле (принцип неопределенности Гейзенберга проясняет этот вопрос!).
8*. Вычислим величину U : |
|
|
|
|
|
||||||||
U = − |
|
(1,6 10−19 )2 |
|
|
|
= − |
256 10−40 |
≈ |
. |
||||
4 0,53 |
10−10 3,14 8,85 10−12 |
58,91268 |
10−22 |
||||||||||
|
|
|
|||||||||||
≈ −4,345414263 10−18 ≈ −4,3 10−18 (Дж). |
|
|
|
|
|||||||||
9*. Ответ: |
U = − |
|
e2 |
|
= −4,3 10−18 Дж ≈ −26,8 эВ. |
|
|||||||
|
|
|
|
||||||||||
|
|
|
|
4aπε0 |
|
|
|
|
|
||||
|
|
*************** |
|
|
|
|
|||||||
Задача 15 |
|
|
|
|
|
|
|
|
|
|
|
||
Одномерная |
нормированная |
волновая |
функция |
||||||||||
|
|
nπ |
|
|
описывает |
состояние |
частицы в |
||||||
ψn ( x) = 2 l sin |
x |
||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
бесконечно глубоком прямоугольном ящике шириной l . Частица находится в возбужденном состоянии ( n = 3). Вычислить
- 68 -

вероятность w нахождения такой частицы в средней трети ящика, то есть когда 3l ≤ x ≤ 23l .
1*. Дано:
ψn (x) = 2 l sin nlπ x ,
n = 3,
3l ≤ x ≤ 23l .
w – ?
Решение.
3*. Анализ задачи. Вероятность w
обнаружения электрона в той или иной части пространства определяется посредством интегрирования квадрата волновой ψ -функции по
соответствующему объему. В случае же одномерной волновой функции интегрирование необходимо вести по одной координате, изменяющейся в заданных пределах. При этом следует учесть, что электрон находится в возбужденном состоянии, описываемом волновой функцией ψ с
соответствующим главным квантовым числом n .
4*. Составим полную систему уравнений для нахождения искомой величины w, обобщив все приведенные выше рассуждения:
(1) |
ψn (x)= |
2 sin nπ x, |
|||||||||
|
|
|
|
|
|
|
|
|
l |
|
l |
w = x∫2 |
|
|
|
|
|
|
|||||
(2) |
|
ψn (x) |
|
2 dx, |
|||||||
|
|
||||||||||
|
|
x1 |
|
|
|
|
|
||||
(3) |
n = 3, |
|
|
|
|||||||
|
|
|
|
l |
|
|
|
|
|
|
|
(4) |
x1 = |
|
|
, |
|
|
|
|
|||
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
(5) |
x2 = |
|
|
2l |
. |
|
|
|
|||
3 |
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Система пяти уравнений (1) – (5) не замкнута, так как содержит шесть неизвестных величин: x1, x2 , l, w, ψ, n.
Однако, данная система имеет однозначное решение относительно искомой величины w ввиду того, что мы имеем дело с
- 69 -
