Методика решения задач по оптике для студентов инженерных специальностей

R = 6,95 108м.

величины m :

Е = σТ4S t,

(1)

m – ?

2

S =

4πR

,

(2)

Вт

Е =

mс2 .

−8

(3)

σ = 5,67 10

,

м2 K4

Система трех уравнений (1) – (3)

c = 3 108 м с.

замкнута, так как содержит три

неизвестные величины: E, S, m .

9*. Ответ:

m ≈ 4,0 109 кг.

***************

1*. Дано:

Решение.

λ = 0,5 мкм = 5 10-7м,

2* ───

4*. Составим полную систему

T =W .

уравнений для

нахождения искомой

величины λ:

W = hν ,

(1)

c =νλ,

(2)

2

T = meυ

υ – ?

(3)

,

h = 6,63 10−34 Дж с,

2

8

W = T .

c = 3 10

м/c ,

(4)

me = 9,1 10-31кг.

9*. Ответ:

υ ≈ 2,0 108м/с.

***************

спектре m = 3

третьего порядка накладывается красная линия

гелия (λ1 = 670 нм)

спектра k = 2 второго порядка?

1*. Дано:

*

Решение.

излучение

a=0

m = 3,

2 .

гелия

D

P

дифракционная решетка

λ1 = 670 нм =

.C

M

линза

N

= 6,7 10-7м,

левая

половина

ϕ

k = 2.

спектральных

линий

не

показана на

экране

λ2 – ?

экран

спектр

линии

λ2

m=0

m=1 m=2

m=3

спектр

линии

λ1

k=0

k=1

k=2

4*. Составим полную систему уравнений для нахождения

искомой величины λ2 :

d (sinϕ −sinα)= mλ2,

(1)

(2)

d (sinϕ −sinα)= kλ .

1

Система двух

уравнений

(1)

–

(2) не

замкнута,

так как

Задача18

Температура

серого тела изменилась при нагревании от

T1 = 1000 K

до T2 = 3000 K . На сколько изменилась длина

1*. Дано:

2* ───

Решение.

T = 1000 K = 103 K ,

1

4*. Составим полную систему

T = 3000 K = 3 103 K ,

уравнений

для нахождения искомой

2

величины

λ:

λ T АЧТ = b,

k1 = 0,9,

(1)

1

1

k2 = 0,8.

(2)

T1 = T1АЧТ 4 k1 ,

λ2T2АЧТ = b,

(3)

(4)

T

= T АЧТ 4

k

2

,

λ – ?

2

2

−3

(5)

λ = λ

− λ

.

2

b = 2,9 10 м К.

1

содержит пять неизвестных величин: λ ,

λ

2

,

λ, ТАЧТ , ТАЧТ .

9*. Ответ:

1

1

2

λ ≈ 1,9 10−6м = 1,9 мкм.

***************

Задача19

Пучок света

с длиной волны λ = 0,49 мкм,

падая на

1*. Дано:

Решение.

λ = 0,49 мкм = 4,9 10-7 м,

α = π 6 рад,

hν

2*.

R = 0,25,

V

α

p = 5 мкПа = 5 10−6 Па,

h

L

α

S = 1,5 м2 ,

S

t =1 c.

n – ?

h = 6,63 10−34 Дж с.

4*. Составим полную систему уравнений для нахождения

искомой величины n:

p = hνn (1 + R)cos2 α,

(1)

0

c = λν,

(2)

n0 = n V ,

(3)

(4)

V = Lcos α S,

L = c t.

(5)

Система пяти уравнений (1) – (5) замкнута, так как

содержит пять неизвестных величины: ν, n0, n, V ,

L.

9*. Ответ:

n ≈ 5,1 1021 .

***************

Задача20

Одномерная

нормированная

волновая

функция

ψn ( x) =

nπ

x

описывает

состояние

частицы

в

2 l sin

l

бесконечно глубоком прямоугольном ящике шириной l = 6 нм

(0 ≤ x ≤ l). Частица находится в возбужденном состоянии ( n = 3).

Определить

координаты

ящика

хi ,

в которых

вероятность

обнаружения

частицы

минимальна.

Пояснить

полученный

- 126 -

результат графически.

1*. Дано:

Решение.

n = 3,

2* ───

(0 ≤ x ≤ l),

4*.

Составим

полную

систему

уравнений

для

нахождения

искомых

l = 6 нм,

величин хi :

ψ2 (x)= 2 sin2 nπ x,

(1)

n

l

l

nπ

dw

2

ψn(x)= 2 l sin

x .

(x),

l

(2)

dx

= ψn

хi – ? ( i = 1,2,...)

(3)

dw

= 0.

dx

Система трех уравнений (1) – (3)

замкнута, так как

содержит три неизвестные величины: x, w, ψ .

9*. Ответ:

x1 = 0 нм, x2 = 2 нм, x3 = 4 нм,

x4 = 6 нм.

***************

Задача21

На какой глубине

H под водой находится водолаз, если он

видит отраженными от поверхности воды те части

горизонтального дна, которые расположены от него на

расстоянии

L ≥ 15 м? Рост водолаза

h = 1,7 м.

Показатель

преломления воды n =1,3.

1*. Дано:

2 *.

Решение.

L ≥ 15 м,

x

nв=1

h = 1,7 м,

B

A

n=1,3

α α

n =1,3.

C

H

H – ?

t

x

h

K

D

L

4*. Составим полную систему уравнений для нахождения

- 127 -

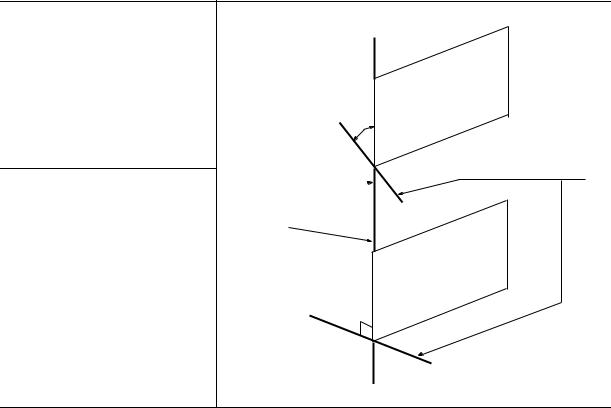
искомой величины H :

x = (H − h) tgα,

(1)

t = H tgα,

(2)

(3)

L = t + x,

1

sinα =

.

(4)

n

Система четырех уравнений (1) –

(4)

замкнута, так как

содержит четыре неизвестные величины: x, H, t, α.

9*. Ответ:

H ≈ 7,0 м.

***************

Задача22

Пластинку оптически активного кристалла толщиной d = 2 мм

поместили между параллельными николями, в результате чего

плоскость поляризации монохроматического света повернулась

на угол ψ = 60o. Какой наименьшей толщины dmin следует взять

пластинку, чтобы поле зрения поляриметра (после второго

николя) стало совершенно темным?

1*. Дано:

Решение.

d = 2 мм = 2 10-3м,

*

2 .

плскость

π

o

поляризации

ψ = 60 =

3 рад.

ψ

света

оптическая ось

(1-ый опыт)

d min – ?

второго николя

оптическая ось

первого николя

плскость

поляризации

θ .

света

(2-ой опыт)

4*.

Составим полную систему уравнений для нахождения

искомой величины d min :

- 128 -