
Методика решения задач по оптике для студентов инженерных специальностей
.pdf
29 |
Одномерная |
нормированная |
волновая |
функция |
||||||||
|
ψn ( x) = |
2 |
nπ |
|
описывает |
состояние частицы в |
||||||
|
l sin |
|
l |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечно |
глубоком |
прямоугольном |
ящике |
шириной |
|||||||
|
l = 6 нм |
(0 ≤ x ≤ l). |
Частица находится |
в |
возбужденном |
|||||||
|
состоянии |
(n = 3). |
Определить координаты |
ящика хi , в |
||||||||
|
которых вероятность обнаружения частицы минимальна. |
|||||||||||
|
Пояснить полученный результат графически. |
|
|
|||||||||
30 |
Одномерная |
нормированная |
волновая |
функция |
||||||||
|
ψn ( x) = |
2 |
nπ |
|
описывает |
состояние частицы в |
||||||
|
l sin |
|
l |
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечно глубоком прямоугольном ящике шириной l . |
|||||||||||
|
Частица |
находится |
в |
возбужденном состоянии |
(n = 4 ). |
|||||||
|
Вычислить вероятность w нахождения такой частицы в |
|||||||||||
|
последней четверти ящика, то есть когда |
3l ≤ x ≤ l . |
||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
31 |
Сферически |
симметричная |
волновая |
функция, |
||||||||
|
описывающая некоторое состояние некоторой частицы, |
|||||||||||
|
имеет вид ψ(r) = Вe -r 2 |
(2d )2 , где r − расстояние частицы |
||||||||||
|
от ядра, |
d = 2Å – |
константа. Определить |
минимальное |
||||||||
|
расстояние rmin рассматриваемой частицы до ядра. |
|||||||||||
32 |
Сферически |
симметричная |
волновая |
функция, |
||||||||
|
описывающая 1s-состояние электрона в атоме водорода, |
|||||||||||
|
имеет вид ψ(r) = Ce -r a , где r − расстояние электрона от |
|||||||||||
|
ядра, |
а = 0,53 10−10 м−первый |
боровский |
радиус. |
||||||||
|
Определить минимальное расстояние rmin электрона до |
|||||||||||
|
ядра. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
***** |
§9 ***** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 110 -

§10. «Усеченные» |
решения задач и ответы |
|||||||||||
|
|
|
|
|
|
Задача1 |
L, |
|
|
|
||
Вычислить |
|
боковое |
смещение |
луча |
вызываемое |
его |
||||||
прохождением через стеклянную пластинку, погруженную в |
||||||||||||
жидкость |
с |
показателем |
преломления |
nж = 1,3. |
Толщина |
|||||||
пластинки |
d = 6 |
см, |
|
показатель преломления nст = 1,5. |
Угол |
|||||||
падения луча α = 60o. |
|
|
|
|
|
|
|
|
|
|||
1*. Дано: |
|
|
|
|
|
|
|
Решение. |
|
|
||
α = 60o = π 3 рад, |
|
|
2 *. A |
|
|
|
|
|
||||
d = 6 cм = 6 10-2 м, |
|
α |
|
|
|
|
||||||
|
|
|
|
|
K |
|
|
.B |
Q |
|
|
|
nж = 1,3, |
|
|
|
|
|
|
|
. |
|
|
N |
|
nст = 1,5. |
|
|
|
|
d |
|
γ |
|
L |
|
|
|
|
|
|
|
|
l |
γ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
. |
|
E |
|
|
L– ? |
|
|
|
|
L |
|
|
. .. |
|
M |
||
|
|
|
|
|
|
O |
C |
F |
|
|||
|
|
|
|
|
|
|
|
|
α |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4*. Составим полную систему уравнений для нахождения |
||||||||||||
искомой величины |
L: |
|
sinα |
|
n |
|
|
|
|
|||
|
|
|
|
|
= |
|
|
|
|
|||
|
|
|
(1) |
|
|
|
ст , |
|
|
|
|
|
|
|
|
|
|
sinγ |
|
nж |
|
|
|
|
|
|
|
|
(2) |
l = d |
cosγ , |
|
|
|
|
|||
|
|
|
(3) |
|
L = l sin(α −γ ). |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система трех уравнений (1) – (3) замкнута, так как |
||||||||||||
содержит три неизвестные величины: γ, l, |
L. |
|
|
|
||||||||
9*. Ответ: |
|
|
L ≈ 1,8 10−2м = 1,8 см. |
|
|
|
||||||
|
|
|
|
*************** |
|
|
|
|
||||
|
|
|
|
|
|
- 111 - |
|
|
|
|
||

|
|
|
Задача2 |
|
|
|
|
Расстояние между предметом и его изображением в выпуклом |
|||||||
зеркале |
L = 30 см. |
Фокусное |
расстояние |
такого |
зеркала |
||
F = 14,3 см. Определить увеличение Г этого зеркала. |
|
||||||
1*. Дано: |
|
|
|
|
Решение. |
|
|
|
|
|
|
2*. |
T |
|
.B |
L = 30 см = 3 10-1 м |
|
|
.M |
|
|||
|
|
|
|
||||
F = 14,3 см = 1,43 10−1м. |
. |
P.B.1 |
.D |
|
.A |
||
|
|
|
F..A1 |
.C |
|
||
|
|
|
O |
|
. K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
Г – ? |
|
|
|
|
f |
d |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
L |
|
4*. Составим полную систему уравнений для нахождения |
|||||||
искомой величины Г : |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
||
(1) |
|
− |
|
|
|
= |
|
|
, |
|
f |
d |
F |
||||||||
|
|
|
|
|||||||
|
|
|
f |
|
|
|
|
|||
|
Г = |
|
|
|
|
|
||||
(2) |
|
|
|
, |
|
|
|
|||
|
d |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
(3) |
L = f + d . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система трех уравнений (1) – (3) замкнута, так как
содержит три неизвестные величины: f , |
d, Г . |
||
9*. Ответ: |
Г ≈ 4,0 10−1 = 0,4. |
|
|
|
*************** |
|
|
|
Задача3 |
|
|
На стеклянный |
клин |
(n =1,5) |
нормально падает |
монохроматический свет. Угол клина равен α = 4′. Определить длину λ световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном
- 112 -
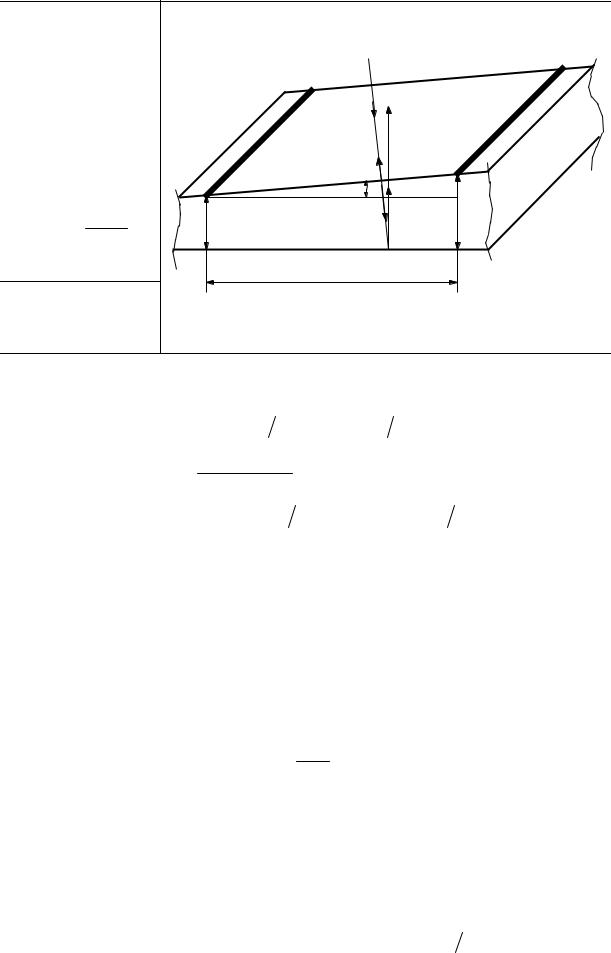
свете равно |
x = 0,2 мм. |
|
|
|
|
|
||||
1*. Дано: |
|
|
|
|
|
|
Решение. |
|
||
x = 0,2 мм = |
2* . |
|
|
|
|
|
|
|||
= 2 10-4 м, |
|
|
|
|
|
2 |
|
|||
n =1,5, |
|
|
|
.A |
|
|
|
1 |
.C |
|
|
|
|
|
|
|
|
α |
|
||
′ |
10 |
−3 |
π . |
|
|
|
|
.B |
|
|
|
hk |
|
|
|
|
hk+1 |
|
|||
α = 4 = |
2,7 |
|
|
|
|
|
|
|||
|
|
k |
|
|
|
|
k+1 |
|
||
|
|
|
|
|
|
|
|
|
||
λ – ? |
|
|
|
|
|
|
x |
|
|
|
4*. Составим полную систему уравнений для нахождения |
||||||||||
искомой величины λ: |
|
|
|
|
|
|
||||
|
|
|
(1) |
2hk n ± λ 2 = (2k +1)λ 2, |
|
|||||
|
|
|
|
(hk +1 − hk )≈ α, |
|
|
|
|||
|
|
|
(2) |
|
|
|
||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
(3) |
2h |
|
n ± λ 2 = (2(k +1)+1)λ 2 . |
|
|||
|
|
|
|
k +1 |
|
|
|
|
|
|
Система трех уравнений (1) – (3) не замкнута, так как |
||||||||||
содержит четыре неизвестные величины: hk , hk +1, k, α. Однако |
||||||||||
уравнения (1) – (3) линейно зависимы относительно переменных |
||||||||||
hk , hk +1, |
k . |
Обозначив hk +1 − hk = θ и вычитая из (3) |
уравнение |
|||||||
(1), получим замкнутую систему двух уравнений с двумя |
||||||||||
неизвестными величинами θ, |
λ: |
|
|
|
||||||
|
|
|
|
|
(4) |
2θ n = λ , |
|
|||
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
(5) |
≈ α . |
|
|
||
|
|
|
|
|
x |
|
|
|||
9*. Ответ: |
|
|
|
|
|
|
|
|||
|
λ ≈ 3,5 10−7м = 350 нм. |
|
||||||||
|
|
|
|
*************** |
|
|
||||
|
|
|
|
|
|
Задача4 |
|
|
||
Три николя расположены так, что угол между главными |
||||||||||
плоскостями первого и |
второго |
равен |
ψ1 = π 4, а |
второго и |
||||||
|
|
|
|
|
|
|
- 113 - |
|
|
|
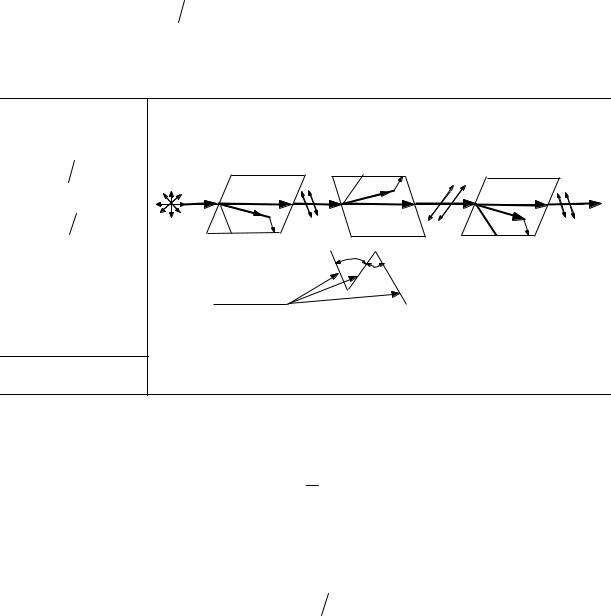
третьего − ψ2 = π 6. |
Определить, |
какую долю η интенсивности |
||||||
естественного света |
обнаружили в интенсивности выходящего |
|||||||
из третьего николя луча, если потерями на отражение и |
||||||||
поглощение можно пренебречь. |
|
|
|
|
||||
1*. Дано: |
|
|
Решение. |
|
|
|||
|
2* . |
|
|
B1 |
|
|
|
|
ψ1 = π 4 рад, |
|
I1e |
|
|
I3e |
|||
B |
o |
I2e |
B2 |
|||||
|
I |
|||||||
|
0 |
|
e |
|
e |
|
e |
|
ψ2 = π 6рад. |
o |
A1 |
o |
|||||
A |
|
ψ1 B1 B2 |
|
A2 |
|
|||
|
|
B |
|
|
||||
|
|
|
|
|
||||
|
|
|
|
ψ2 |
|
|
|
|
|
|
|
|
A A1 |
A2 |
|
|
|
|
|
оптические |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
оси |
|
|
|
|
|
|
η – ? |
|
|
|
|
|
|
|
|
4*. |
Составим полную систему уравнений для нахождения |
|||||||
искомой величины η : |
|
|
|
|
|
|
||
|
I1e = |
1 |
I0 , |
|
(1) |
2 |
|||
|
|
|
||
I2e = I1e cos2 ψ1, |
||||
(2) |
||||
|
I3e = I2e cos2 ψ2 , |
|||
(3) |
||||
|
η = I3e I0 . |
|||
(4) |
||||
Система четырех уравнений (1) – (4) не замкнута, так как содержит пять неизвестных величин: I0, I1e , I2e , I3e , η.
Однако уравнения (1) – (4) линейно зависимы относительно переменных I0, I1e , I2e , I3e . Решение системы получается
последовательной подстановкой (1) в (2), далее в (3) и т.д., что приводит к единственному уравнению с одним неизвестным.
9*. Ответ: |
η ≈ 2,0 10−1 = 0,2. |
***************
Задача5
Вычислить энергию Q , излучаемую за промежуток времени
t = 1 мин, с поверхности черного тела площадью S = 10 см2 , температура которого T = 1002°C и степень черноты k = 0,7.
- 114 -
|
1*. Дано: |
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
t = 1 мин = 60 c , |
|
|
|
|
|
2* ─── |
|
|
|
|
||
|
S = 10 см2 = 10−3 м2 , |
|
|
|
4*. Составим полную систему |
||||||||
|
|
|
|
уравнений для |
нахождения |
искомой |
|||||||
|
T = 1002°C , |
|
|
|
|
|
|
|
величины Q : |
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = kσT |
′4 |
, |
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
||
|
k = 0,7 . |
|
|
|
|
|
|
|
(2) |
T′ =T + 273, |
|
||
|
|
|
|
|
|
|
|
|
(3) |
Q = εSt. |
|
|
|
|
Q – ? |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
трех уравнений (1) – |
||||
|
|
|
|
|
|
|
|
|
Система |
||||
|
σ = 5,67 10 |
−8 |
Вт |
|
. |
|
(3) замкнута, так как содержит три |
||||||
|
|
|
неизвестные величины: Q, ε, |
T′. |
|||||||||
|
|
м |
2 |
K |
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
9*. Ответ: |
|
|
|
Q ≈ 6,3 103 Дж = 6,3 кДж. |
|
|
|
|||||
|
|
|
|
|
|
|
|
*************** |
|
|
|
|
|
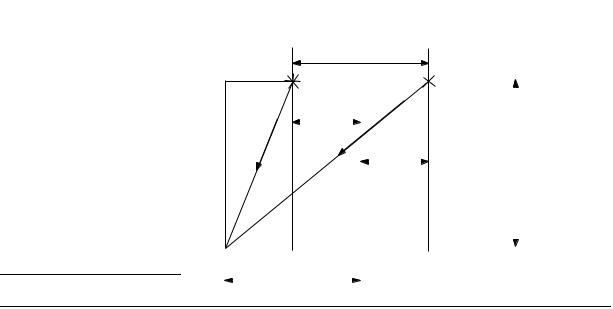
Задача6
В опыте Юнга расстояние между щелями d = 1 мм, а расстояние от щелей до экрана равно L = 3 м. Определить расстояние S , отсчитываемое от центра интерференционной картины, до третьей темной полосы ( m = 3), если щели освещать монохроматическим светом с длиной волны λ = 0,5 мкм.
1*. Дано: |
−3 |
|
|
|
|
|
2 *. |
|
|
|
Решение. |
|
|
|
|
||||
d = 1 мм = 10 |
м, |
|
|
|
|
|
|
|
|
d |
. |
|
|
|
|
|
|||
|
|
|
. |
S1 |
. |
. |
S |
|
|
|
|
||||||||
|
|
|
|
C |
|
|
|
N |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
L = 3 м, |
|
|
|
|
|
|
|
|
|
d/2 |
|
|
|
|
|
|
|
|
|
m = 3 , |
|
|
|
|
|
|
r1 |
|
|
r2 |
|
|
d/2 |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
λ = 0,5 мкм = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
. |
k=2. . |
|
|
. . . |
|
|
|
|||||||||||
= 5 10−7 м. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
M |
|
|
|
|
|
O |
|
|
|
|
|
экран |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
k=3 |
|
|
|
k=1 |
|
k=0 |
k=1 k=2 k=3 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
S – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4*. Составим полную систему уравнений для нахождения искомой величины S :
- 115 -
(1) |
r2 |
= L2 |
+(S −d 2)2, |
|||
|
1 |
|
|
|
|
|
2 |
2 |
|
2 |
|||
|
|
|||||
(2) |
r2 |
= L |
+(S + d 2) |
, |
||
|
= (2m +1) |
λ |
|
|
||
(3) |
, |
|
||||
2 |
|
|||||
|
|
|
|
|
|
|
|
= r2 − r1. |
|
|
|
||
(4) |
|
|
|
|||
Система четырех уравнений (1) – (4) замкнута, так как
содержит четыре неизвестные величины: r1, |
r2, |
, |
S. |
|
|
|
|||||||||||
9*. Ответ: |
|
S ≈ 5,3 10−3м = 5,3 мм. |
|
|
|
|
|
|
|||||||||
|
|
|
|
*************** |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Задача7 |
|
|
|
|
|
|
|
|
|
||
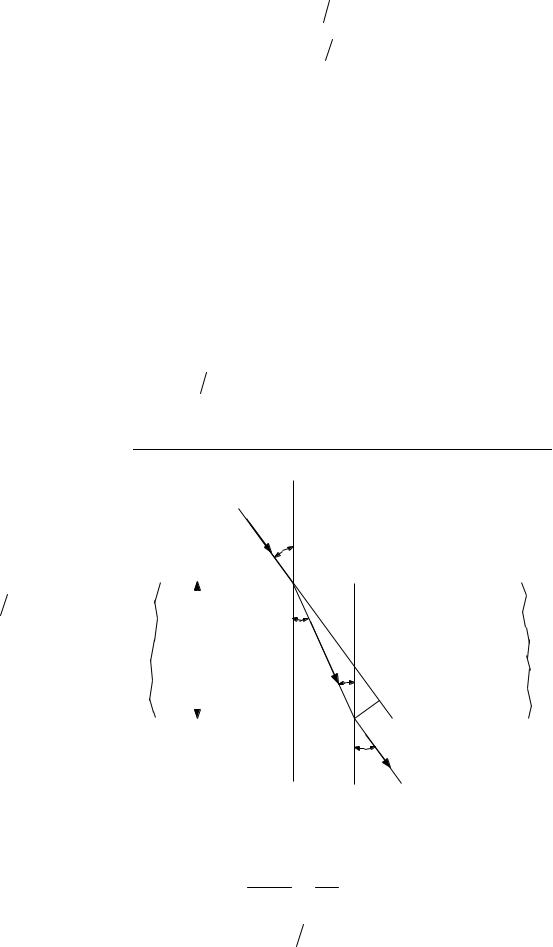
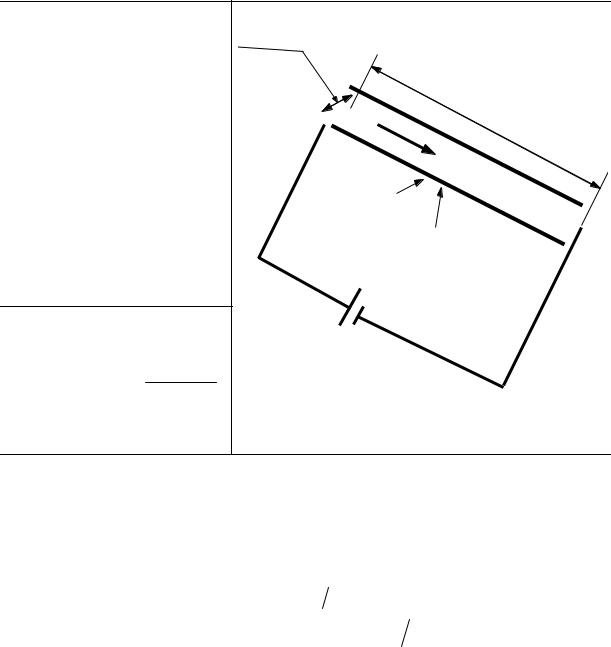
|
Луч падает |
на |
плоскопараллельную |
пластинку толщиной |
|||||||||||||
|
h = 1 мм, находящуюся в среде |
с |
показателем |
преломления |
|||||||||||||
|
n1 =1, |
под |
углом |
α = π 6 рад. |
Определить |
геометрическую |
|||||||||||
|
длину пути L луча в пластинке, если ее показатель преломления |
||||||||||||||||
|
n2 =1,5 . |
|
|
|
|
|
|
Решение. |
|
|
|
|
|
||||
|
1*. Дано: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
h = 1 мм = 10-3м, |
* |
A |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 . |
|
α |
|
|
|
|
|
|
|
|
|
||
|
n1 =1, |
|
|
|
|
|
|
|
|
. |
|
|
n |
|
|
|
|
|
|
|
|
K |
|
.B |
|
|
|
N |
|||||||
|
|
|
|
|
|
|
|
|
1 |
||||||||
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|||
|
α = π 6 рад, |
|
|
|
|
|
|
γ |
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
h |
|
|
|
L |
|
|
|
|
|
|
|
|
|
n2 =1,5 . |
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
. .. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
L |
|
O |
|
|
C |
F |
|
|
M |
|
||
|
L – ? |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
α |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4*. |
Составим полную систему уравнений для нахождения |
||||||||||||||||
искомой величины L: |
sinα |
|
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
2 , |
|
|
|
|
|
|
||||
|
|
|
|
|
(1) |
sinγ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
L = h cosγ . |
|
|
|
|
|
|
|||||
|
|
|
|
|
(2) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
- 116 - |
|
|
|
|
|
|
|
|
|
|
Система двух уравнений (1) – (2) замкнута, так как содержит |
||||||||||
две неизвестные величины: γ, |
L. |
|
|
|
||||||
9*. Ответ: |
|
|
L ≈ 1,1 10−3м = 1,1 мм. |
|
|
|||||
|
|
|
|
|
*************** |
|
|
|
||
|
|
|
|
|
|
Задача8 |
|
|
|
|
В электрической лампочке |
диаметр |
вольфрамовой |
спирали |
|||||||
d = 0,3 мм, |
|
а длина – |
L = 5 см. При включении лампочки в |
|||||||
сеть напряжением U = 220 B по спирали течет ток I = 0,5 A. |
||||||||||
Найти |
температуру |
T |
спирали, предполагая, что степень |
|||||||
черноты вольфрамовой спирали равна k = 0,8. |
|
|||||||||
1*. Дано: |
|
|
|
|
|
Решение. |
|
|||
d = 0,3 мм = |
|
|
|
d |
2*. |
|
|
|
||
= 3 10−4м, |
|
|
|
|
0 |
|
L |
|
||
|
|
|
|
|
|
|
|
|
||
L = 5 см = 5 10−2м, |
|
|
|
I |
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
U = 220 B , |
|
|
|
|
|
k |
|
0 |
||
I = 0,5 A , |
|
|
|
|
|
U |
|
T |
||
k = 0,8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T – ? |
|
|
|
|
|
|
|
|
|
|
σ = 5,67 10 |
− |
8 |
Вт |
. |
|
|
|
|
|
|
|
|
м2 K4 |
2*. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4*. |
Составим полную систему уравнений для нахождения |
|||||||||
искомой величины T : |
|
ε(T )= kσT 4, |
|
|
|
|||||
|
|
|
|
(1) |
|
|
|
|||
|
|
|
|
|
|
P = IU, |
|
|
|
|
|
|
|
|
(2) |
|
|
|
|||
|
|
|
|
(3) |
ε(T )= P S , |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = |
πdL + 2 πd |
2 |
4. |
|
|
|
|
|
(4) |
|
|
||||
Система |
четырех уравнений (1) – |
(4) замкнута, |
так как |
|||||||
|
|
|
|
|
|
|
- 117 - |
|
|
|
содержит четыре неизвестные величины: ε, |
T, P, |
S . |
|
|||||
9*. Ответ: |
|
T ≈ 3,2 103 K. |
|
|
|
|||
|
|
|
*************** |
|
|
|
||
|
|
|
Задача9 |
|
|
|
|
|
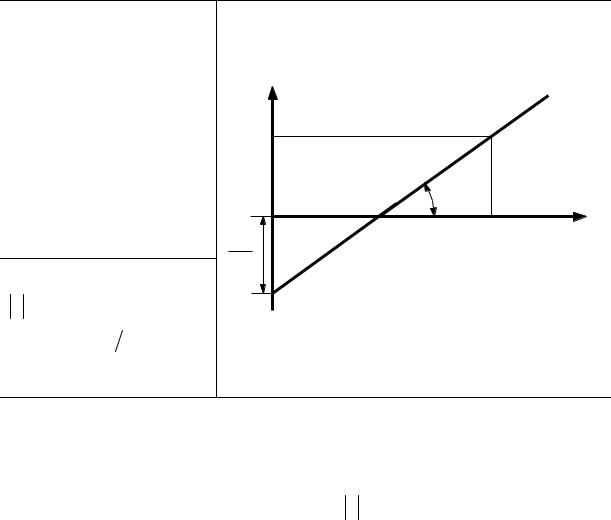
Калий освещается белым светом с граничными длинами волн |
||||||||
λф = 390 нм |
и |
λкр = 760 нм. |
Определить |
наименьшее |
||||
задерживающее |
|
напряжение |
Umin , |
при |
котором |
фототок |
||
прекратится. Работа выхода электронов с поверхности калия |
||||||||
равна A = 2,2 эВ. |
|
|
|
|
|
|||
1*. Дано: |
|
2*. |
|
Решение. |
|
|
||
λф = 390 нм = |
|
|
|
|
|
|
||
= 3,9 10-7м, |
|
U , B |
|
|
|
|
||
λкр = 760 нм = |
|
U |
з |
|
|
|
|
|
|
|
|
|
|
|
|||
= 7,6 10-7м, |
|
min |
|
|
|
|
|
|
|
|
α=arctg h/e |
|
. |
|
|||
A = 2,2 эВ = 2,2 |
|
|
|
|||||
1,6 10-19 Дж. |
A |
. |
. |
α |
ν, 1/c |
|||
|
|
|
νкр |
νгр |
=A/h |
νф |
||
Umin – ? |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e = 1,6 10-19 Кл, |
|
|
|
|
|
|
||
c = 3 108 м с, |
|
|
|
|
|
|
|
|
h = 6,63 10−34 Дж с. |
|
|
|
|
|
|||
4*. |
Составим полную систему уравнений для нахождения |
|||||||
искомой величины Umin : |
hν = A +T , |
|
|
|
||||
|
|
|
(1) |
|
|
|
||
|
|
|
|
T = eUmin , |
|
|
|
|
|
|
|
(2) |
|
|
|
||
|
|
|
|
ν =νф, |
|
|
|
|
|
|
|
(3) |
|
|
|
||
|
|
|
|
с =νф λф. |
|
|
|
|
|
|
|
(4) |
|
|
|
||
Система четырех уравнений (1) – (4) замкнута, так как |
||||||||
содержит четыре неизвестные величины: ν , T , Umin , νф. |
||||||||
9*. Ответ: |
|
Umin ≈ 1,0 В. |
|
|
|
|||
|
|
|
*************** |
|
|
|
||
|
|
|
|
- 118 - |
|
|
|
|

Задача10
Два плоских зеркала образуют двугранный угол. На одно из зеркал под некоторым углом падает световой луч, лежащий в плоскости, перпендикулярной ребру двугранного угла. После однократного отражения от каждого из зеркал этот луч «прочерчивает» треугольник, пересекая первоначальный луч в
некоторой |
точке F и образуя угол при вершине |
F β =150o. |
|||||||||||
Определить величину δ двугранного угла. |
|
|
|||||||||||
1*. Дано: |
|
|
* |
|
|
|
|
Решение. |
|
|
|||
|
|
|
|
|
|
|
|
||||||
o |
5π |
|
|
|
|
|
|
|
S-источник |
|
|||
β = 150 |
= |
|
рад. |
2. |
|
|
|
F |
|
|
|||
6 |
.α |
|
|
|
|
||||||||
|
|
|
|
.β |
. |
π−α−2γ |
|||||||
|
|
|
|
|
|
α |
|
||||||
|
|
|
|
.K |
B |
|
|
|
|
N |
.M |
|
|
|
|
|
|
|
|
π/2−α |
|
γγ |
π/2−γ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ |
|
ребро |
|
|
|
|
|
|
|
|
|
|
O. |
|
||||
|
|
|
|
|
|
|
|
двугранного |
|||||
|
|
|
|
|
|
|
|
|
|
|
угла |
|
|
4*. Составим |
полную систему уравнений для нахождения |
||||||||||||
искомой величины δ: |
|
|
|
|
|
|
|
(OKFM) |
|||||
(1) |
|
β + δ+ π 2 + α+π 2 + γ = 2π, |
|
|
|||||||||
(2) |
δ+ π 2 +π − 2γ −α+ π 2 + γ = 2π, |
(OKNM) |
|||||||||||
(3) |
δ+ π 2 −α + π 2 −γ = π. |
|
|
(OKM) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система трех уравнений (1) – (3) замкнута, так как |
|||||||||||||
содержит три неизвестных величины: δ, α, γ. |
|
|
|||||||||||
9*. Ответ: |
|
|
δ = |
|
π |
|
рад. |
|
|
|
|
||
|
|
12 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
***************
- 119 -
