4 Математичні схеми моделювання систем

4.1 Безперервно- детерміновані моделі ( D- схеми )

Розглянемо особливості безперервно-детермінованого підходу на прикладі використання в якості математичних моделей диференціальних рівнянь.

Зазвичай в таких математичних моделях незалежною змінною, від якої залежать невідомі шукані функції, служить час t. Тоді математичне співвідношення для детермінованих систем в загальному вигляді буде

де y' = dy/dt, y = (y₁, у₂, ..., у_п) и f = (f₁,f₂,…,f_n) - n-мірні вектори; f(y, t) — вектор-функція, яка визначена на деякій (п+ 1) - мірній (у, t) множині і є безперервною.

Оскільки математичні схеми такого вигляду відображають динаміку системи, що вивчається, тобто її поведінку в часі, то вони називаються

D-схемами (англ. dynamic) .

У простому випадку звичайне диференціальне рівняння має вигляд

Найбільш важливе для системотехніки застосування D-схем як математичний апарат в теорії автоматичного управління.

Для ілюстрації особливостей побудови і застосування D-схем розглянемо простий приклад формалізації процесу функціонування двох елементарних систем різної фізичної природи: механічної S_М (коливання маятника) і електричної S_K (коливальний контур).

Процес малих коливань маятника описується звичайним диференціальним рівнянням

де т_м, l_М — маса і довжина підвісу маятника; g — прискорення вільного падіння; θ(t) - кут відхилення маятника у момент часу t.

З цього рівняння вільного коливання маятника можна знайти оцінки характеристик, які цікавлять. Наприклад, період коливання маятника

Аналогічно, процеси в електричному коливальному контурі описуються звичайним диференціальним рівнянням

де L_K, С_K — індуктивність і ємкість конденсатора; q (t) — заряд конденсатора у момент часу t.

З цього рівняння можна отримати різні оцінки характеристик процесу в коливальному контурі. Наприклад, період характеристичних коливань

Очевидно, що, ввівши позначення h_o = m_M l ²_M = L_K, h₁ = 0, h₂ = m_M g l_M = 1/С_K, θ(t) = q(t)=z(t), отримаємо звичайне диференціальне рівняння другого порядку, що описує поведінку цієї замкнутої системи:

(4.1)

де h₀, h₁ , h₂ — параметри системи; z(t) — стан системи у момент часу t.

Таким чином, поведінка цих двох об'єктів може бути досліджена на основі загальної математичної моделі (4.1). Крім того, необхідно відзначити, що поведінка однієї з систем може бути проаналізоване за допомогою іншої. Наприклад, поведінка маятника (системи S_М) може бути вивчене за допомогою електричного коливального контура (системи S_К).

Якщо система S, що вивчається, тобто маятник або контур, взаємодіє із зовнішнім середовищем Е, то з'являється вхідна дія x(t) (зовнішня сила для маятника і джерело енергії для контура) і безперервно-детермінована модель такої системи матиме вигляд

З погляду загальної схеми математичної моделі х(t) є вхідною (управляючою) дією, а стан системи S в даному випадку можна розглядати як вихідну характеристику, тобто вважати, що вихідна змінна співпадає із станом системи в даний момент часу у = z.

4.2 Безперервно- стохастичні моделі ( Q- схеми )

Особливості безперервно-стохастичного підходу розглянемо на прикладі використання в якості типових математичних схем систем масового обслуговування (англ. queueing system), які називатимемо Q-схемами. Системи масового обслуговування є класом математичних схем, розроблених в теорії масового обслуговування і різних застосуваннях для формалізації процесів функціонування систем, які за своєю суттю є процесами обслуговування. Системи масового обслуговування - це такі системи, в які у випадкові моменти часу поступають заявки на обслуговування. Заявки, що при цьому поступили, обслуговуються за допомогою каналів обслуговування, що є у розпорядженні системи.

В якості процеса обслуговування можуть бути представлені різні по своїй фізичній природі процеси функціонування економічних, виробничих, технічних і інших систем, наприклад потоки постачань продукції деякому підприємству, потоки деталей і комплектуючих виробів на складальному конвеєрі цеху, заявки на обробку інформації ЕОМ від віддалених терміналів і так далі. При цьому характерною для роботи таких об'єктів є випадкова поява заявок (вимог) на обслуговування і завершення обслуговування у випадкові моменти часу, тобто стохастичний характер процесу їх функціонування. Зупинимося на основних поняттях масового обслуговування, необхідних для використання Q-схем, як при аналітичному, так і при імітаційному.

У будь-якому елементарному акті обслуговування можна виділити дві основні складові: очікування обслуговування заявкою і власне обслуговування заявки. Це можна зобразити у вигляді деякого i-го приладу обслуговування П_i (рис. 4.1), що складається з накопичувача заявок H_i (черга), і каналу обслуговування заявок (або просто каналу) K_i. На кожен елемент приладу обслуговування П_i поступають потоки подій: у накопичувач H_i — потік заявок w_i, на канал K_i — - потік обслуговувань u_i.

Потоком подій називається послідовність подій, що відбуваються одне за іншим в якісь випадкові моменти часу. Розрізняють потоки однорідних і неоднорідних подій. Потік подій називається однорідним, якщо він характеризується тільки моментами надходження цих подій (моментами появи) і задається послідовністю

{t_n} = {0 ≤ t₁ ≤ t₂ ≤ ... ≤ t_n ≤ ... }, де t_n — момент настання n-ї події — ненегативне дійсне число. Однорідний потік подій також може бути заданий у вигляді послідовності проміжків часу між n-м і (n-1) -м подіями {τ_n}.

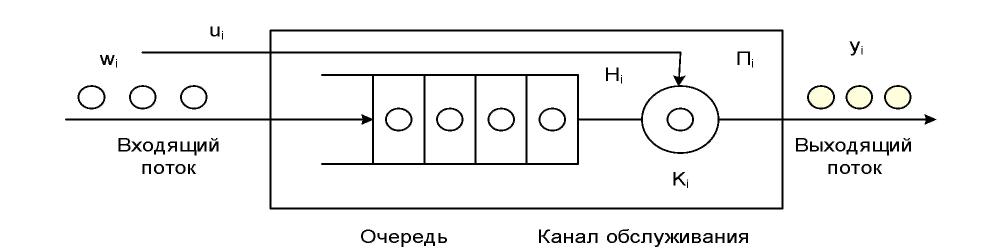
Рис. 4.1 Прилад обслуговування

Потоком неоднорідних подій називається послідовність (t_n, f_n), де t_n -вызывающие моменти; f_n — набір ознак події. Наприклад, стосовно процесу обслуговування для неоднорідного потоку заявок можуть бути задані приналежність до того або іншого джерела заявок, наявність пріоритету, можливість обслуговування тим або іншим типом каналу і тому подібне

Приклад потоку подій приведений на рис. 4.2, де позначене T_j - інтервал між подіями (випадкова величина); T_H - час спостереження, T_с - момент здійснення події.

Рис. 4.2 Схема потоку подій

Якщо T_j = const або визначено якою-небудь формулою T_j = f(T_j-1 ), то потік називається детермінованим. Інакше потік називається випадковим.

Заявки, обслужені каналом і заявки, що покинули прилад, з різних причин необслуженими (наприклад, через переповнювання накопичувача), утворюють вихідний потік. Інтервали часу між моментами виходу заявок утворюють підмножину вихідних змінних.

Процес функціонування пристрою обслуговування, можна представити як процес зміни станів його елементів в часі z_i(t). Перехід в новий стан системи означає зміна кількості заявок, які в нім знаходяться (у пристрої обслуговування і в черзі).

У практиці моделювання систем, що мають складніші структурні зв'язки і алгоритми поведінки, для формалізації використовуються не окремі прилади обслуговування, а Q-схемы, що утворюються композицією багатьох елементарних приладів обслуговування (мережі масового обслуговування). Якщо канали різних приладів обслуговування сполучені паралельно, то має місце багатоканальне обслуговування (багатоканальна Q-схема), а якщо прилади і їх паралельні композиції сполучені послідовно, то має місце багатофазне обслуговування (багатофазна Q-схема). Таким чином, для завдання Q-схемы необхідно використовувати оператор сполучення R, що відображає взаємозв'язок елементів структури (каналів і накопичувачів) між собою.

Зв'язки між елементами Q-схемы зображають у вигляді стрілок (ліній потоку, що відображають напрям руху заявок). Розрізняють розімкнені і замкнуті Q-схеми. У розімкненій Q-схемі вихідний потік обслужених заявок не може знову поступити на який-небудь елемент, тобто зворотній зв'язок відсутній, а в замкнутих Q-схемах є зворотні зв'язки, по яких заявки рухаються в напрямі, зворотному руху вхід-вихід.

Для завдання Q-схемы також необхідно описати алгоритми її функціонування, які визначають набір правил поведінки заявок в системі в різних неоднозначних ситуаціях. Залежно від місця виникнення таких ситуацій розрізняють алгоритми (дисципліни) очікування заявок в накопичувачі (черзі) і обслуговування заявок каналом кожного елементарного обслуговуючого приладу Q-схемы. Неоднорідність заявок, що відображає процес в тій або іншій реальній системі, враховується за допомогою введення класів пріоритетів.

Виходячи з правил вибору заявок з накопичувача H_i на обслуговування каналом K_i можна виділити відносні і абсолютні пріоритети. Відносний пріоритет означає, що заявка з вищим пріоритетом, що поступила в накопичувач, чекає закінчення обслуговування попередньої заявки каналом, і лише після цього займає канал. Абсолютний пріоритет означає, що заявка з вищим пріоритетом, що поступила в накопичувач перериває обслуговування каналом заявки з нижчим пріоритетом і сама займає канал (при цьому витіснена з каналу обслуговування заявка може або покинути систему, або може бути знову записана на якесь місце в накопичувач).

4.3 Дискретно-детерміновані моделі ( F - схеми)

Особливості дискретно-детермінованого підходу на етапі формалізації процесу функціонування систем розглянемо на прикладі використання в якості математичного апарату теорії автоматів. Теорія автоматів - це розділ теоретичної кібернетики, в якому вивчаються математичні моделі - автомати. На основі цієї теорії система представляється у вигляді автомата, що переробляє дискретну інформацію і що міняє свої внутрішні стани лише в допустимі моменти часу. Поняття «автомат» варіюється залежно від характеру систем, що конкретно вивчаються, від прийнятого рівня абстракції і доцільного ступеня спільності.

Автомат можна представити як деякий пристрій (чорний ящик), на який подаються вхідні сигнали і знімаються вихідні і який може мати деякі внутрішні стани. Кінцевим автоматом називається автомат, у якого безліч внутрішніх станів і вхідних сигналів (а отже, і безліч вихідних сигналів) є кінцевими множинами.

Абстрактно кінцевий автомат (англ. finite automata) можна представити як математичну схему ( F-схему ), що характеризується шістьма елементами: кінцевою множиною X вхідних сигналів (вхідним алфавітом); кінцевою множиною Y вихідних сигналів (вихідним алфавітом); кінцевою множиною Z внутрішніх станів (внутрішнім алфавітом або алфавітом станів); початковим станом z₀, z_o є Z; функцією переходів φ (z, х); функцією виходів ψ (z, x). Автомат, що задається F-схемой: F=(Z, X, Y, φ, ψ, z_o) - функціонує в дискретному автоматному часі, моментами якого є такти, тобто рівні інтервали часу, що примикають один до одного, кожному з яких відповідають постійні значення вхідного і вихідного сигналів і внутрішні стани. Позначимо стан, а також вхідний і вихідний сигнали, відповідні t-му такту при t = 0, 1, 2 ..., через z(t), x(t), у(t). При цьому, по умові, z(0)=z_o, а z(t) є Z, x(t) є X, у(t) є Y.

Абстрактний кінцевий автомат має один вхідний і один вихідний канали. У кожен момент t = 0, 1, 2 ... дискретного часу F-автомат знаходиться в певному стані z(t) з безлічі Z станів автомата, причому в початковий момент часу t=0 він завжди знаходиться в початковому стані z(0)=z_o. У момент t, будучи в стані z(t), автомат здатний сприйняти на вхідному каналі сигнал x(t) є X і видати на вихідному каналі сигнал y(t) =ψ [z (t), x (t)], переходячи в стан z (t +1) = φ [z (t), x (t)], z (t) є Z, у (t) є Y. Абстрактний кінцевий автомат реалізує деяке відображення множини слів вхідного алфавіту X на множину слів вихідного алфавіту Y. Іншими словами, якщо на вхід кінцевого автомата, встановленого в початковий стан z₀, подавати в деякій послідовності букви вхідного алфавіту х(0), х(1), х(2) ..., тобто вхідне слово, то на виході автомата послідовно з'являтимуться букви вихідного алфавіту у(0), у(1), у(2) ..., утворюючи вихідне слово.

Таким чином, робота кінцевого автомата відбувається по наступній схемі: у кожному t-м такті на вхід автомата, що знаходиться в стані z(t), подається деякий сигнал x(t), на який він реагує переходом в (t+1) -му такті в новий стан z(t+1) і видачею деякого вихідного сигналу. Сказане вище можна описати наступними рівняннями:

для F – автомата першого роду, званого також автоматом Мілі

(4.2)

(4.3)

для F – автомата другого роду:

(4.4)

(4.5)

Автомат другого роду, для якого

тобто функція виходів не залежить від вхідної змінної x(t), називається автоматом Мура.

По числу станів розрізняють кінцеві автомати з пам'яттю і без пам'яті. Автомати з пам'яттю мають більш за один стан, а автомати без пам'яті (комбінаційні або логічні схеми) володіють лише одним станом. Робота комбінаційної схеми полягає в тому, що вона ставить у відповідність кожному вхідному сигналу x(t) певний вихідний сигнал у(t), тобто реалізує логічну функцію вигляду

Ця функція називається булевою, якщо алфавіти X і У, яким належать значення сигналів х і у, складаються з двох букв.

По характеру відліку дискретного часу кінцеві автомати діляться на синхронні і асинхронні. У синхронних F-aвmoматах моменти часу, в які автомат «прочитує» вхідні сигнали, визначаються примусово синхронізуючими сигналами. Після чергового синхронізуючого сигналу з урахуванням «считаного» і відповідно до рівнянь (4.2) — (4.5) відбувається перехід в новий стан і видача сигналу на виході, після чого автомат може сприймати наступне значення вхідного сигналу. Таким чином, реакція автомата на кожне значення вхідного сигналу закінчується за один такт, тривалість якого визначається інтервалом між сусідніми синхронізуючими сигналами. Асинхронний F-автомат прочитує вхідний сигнал безперервно, і тому, реагуючи на достатньо довгий вхідний сигнал постійної величини х, він може, як випливає з (4.2) — (4.5), кілька разів змінювати стан, видаючи відповідне число вихідних сигналів, поки не перейде в стійке, яке вже не може бути змінене даним вхідним сигналом.

Щоб задати кінцевий F-автомат, необхідно описати всі елементи множини F= ( Z, X, Y,φ, ψ, z_o) тобто вхідний, внутрішній і вихідний алфавіти, а також функції переходів і виходів, причому серед множини станів необхідно виділити стан z_0, в якому автомат знаходився у момент часу t=0. Існує декілька способів завдання роботи F-автоматів, але найчастіше використовуються табличний, графічний і матричний.

Простий табличний спосіб завдання кінцевого автомата заснований на використанні таблиць переходів і виходів, рядки яких відповідають вхідним сигналам автомата, а стовпці - його станам.

При іншому способі завдання кінцевого автомата використовується поняття направленого графа. Граф автомата є набором вершин, відповідних різним станам автомата, і дуг графа, що сполучають вершини, відповідних тим або іншим переходам автомата.

При вирішенні завдань моделювання систем часто зручнішою формою є матричне завдання кінцевого автомата. При цьому матриця з'єднань автомата є квадратна матриця С=||сij||, рядки якої відповідають початковим станам, а стовпці — станам переходу.

Таким чином, поняття F-автомата в дискретно-детермінованому підході до дослідження на моделях властивостей об'єктів є математичною абстракцією, зручною для опису широкого класу процесів функціонування реальних об'єктів в автоматизованих системах обробки інформації і управління. Як такі об'єкти в першу чергу слід назвати елементи і вузли ЕОМ, пристрої контролю, регулювання і управління, системи часової і просторової комутації в техніці обміну інформацією і так далі. Для всіх перерахованих об'єктів характерна наявність дискретних станів і дискретний характер роботи в часі, тобто їх опис за допомогою F-схем є ефективним. Але широта їх застосування не означає універсальності цих математичних схем. Наприклад, цей підхід непридатний для опису процесів ухвалення рішень, процесів в динамічних системах з наявністю перехідних процесів і стохастичних елементів.

4.4 Дискретно-стохастичні моделі (P-схеми)

Розглянемо особливості побудови математичних схем при дискретно-стохастичному підході до формалізації процесу функціонування досліджуваної системи S. Оскільки суть дискретизації часу при цьому підході залишається аналогічною розглянутим в 4.3 кінцевим автоматам, той вплив чинника стохастичності прослідкуємо також на різновиді таких автоматів, а саме на імовірнісних (стохастическиих) автоматах.

У загальному вигляді імовірнісний автомат (англ. probabilistic automat) можна визначити як дискретний потактный перетворювач інформації з пам'яттю, функціонування якого в кожному такті залежить тільки від стану пам'яті в нім і може бути описане статистично.

Застосування схем імовірнісних автоматів (Р-схем) має важливе значення для розробки методів проектування дискретних систем, що проявляють статистично закономірну випадкову поведінку, для з'ясування алгоритмічних можливостей таких систем в обгрунтування меж доцільності їх використання, а також для вирішення завдань синтезу по вибраному критерію дискретних стохастичних систем, які задовольняють заданим обмеженням.

Введемо математичне поняття Р-автомата, використовуючи поняття, введені для F-автомата. Розглянемо множину G, елементами якої є всілякі пари (х_i, z_s), де х_i і z_s - елементи вхідної підмножини X і підмножини станів Z відповідно. Якщо існують дві такі функції φ і ψ, і з їх допомогою здійснюються відображення G → Z і G → Y, то говорять, що F=(Z, X, Y,φ, ψ) визначає автомат детермінованого типу.

Введемо в розгляд більш загальну математичну схему. Хай Ф - множина всіляких пар виду (z_k, у_j), де у_j - елемент вихідної підмножини Y. Зажадаємо, щоб будь-який елемент множини G індукував на множині Ф деякий закон розподілу наступного вигляду:

Елементи з Ф …(z₁ y₁) … (z₁ y₂) … … (z_K y_J-1)(z_K y_J) (х_i z_s ) … b₁₁ b ₁₂ … b_K(J-1) b_kJ .

При цьому де b_kj — вірогідність переходу автомата в стан z_k і появи на виході сигналу у_j якщо він був в змозі z_s, і на його вхід у цей момент часу поступив сигнал x_i. Число таких розподілів, представлених у вигляді таблиць, рівне числу елементів множини G. Позначимо множину цих таблиць через В. Тоді четвірка елементів P=(Z, X, Y, В) називається імовірнісним автоматом (Р-автоматом).

Хай елементи множини G індукують деякі закони розподілу на підмножинах Y і Z, що можна представити відповідно у вигляді:

Елементи з У … y₁ … y₂ … y _{J - 1} … y _J

(x_i, z_s) … q₁ … q₂ … q _{J - 1} … q _J

Елементи з Z … z₁ … z₂ … z _{k - 1} … z _k

(x_i, z_s) … z₁ … z₂ … z _{k - 1} … z _k

При цьому і де z_k і q_k — вірогідність переходу Р- автомата в стан z_k і появи вихідного сигналу у_к за умови, що Р-автомат знаходився в стані z_s і на його вхід поступив вхідний сигнал x_i.

Якщо для всіх k і j має місце співвідношення q_k z_i = b_kj, то такий Р-автомат називається імовірнісним автоматом Мілі. Ця вимога означає виконання умови незалежності розподілів для нового стану Р-автомата і його вихідного сигналу.

Хай тепер визначення вихідного сигналу Р-автомата залежить лише від того стану, в якому знаходиться автомат в даному такті роботи. Іншими словами, хай кожен елемент вихідної підмножини Y індикує розподіл вірогідності виходів, що має наступний вигляд:

Елементи з У … y₁ … y₂ … y_k-1 … y_k (x_i, z_s) … s₁ … s₂ … s_I-1 … s_I

Тут де s_i — вірогідність появи вихідного сигналу y_s за умови, що Р-автомат знаходився в стані z_k.

Якщо для всіх k і i має місце співвідношення z_k s_i = b_ki, то такий Р-автомат називається імовірнісним автоматом Мура. Поняття Р-автоматів Мілі і Мура введене по аналогії з детермінованим F-автоматом, який задається F= (Z, X, Y, φ,ψ). Окремим випадком Р-автомата, що задається як Р= (Z. X, Y, В), є автомати, у яких або перехід в новий стан, або вихідний сигнал визначаються детерміновано. Якщо вихідний сигнал Р-автомата визначається детерміновано, то такий автомат називається Y-детерминированным імовірнісним автоматом. Аналогічно, Z-детерминированным імовірнісним автоматом називається Р-автомат, у якого вибір нового стану є детермінованим.