5.Тангенциальное и нормальное ускорение

Вектор – ускорение материальной точки – характеризует быстроту изменения ее скорости как по модулю, так и по направлению.Поэтому часто вместо выражения вектора ускорения через три его проекции на оси координат удобнее представлять его в виде геометрической суммы только двух составляющих, направленных по касательной и нормали к траектории. При этом составляющая, направленная по касательной к траектории и называемая тангенциальным (касательным) ускорением, будет характеризовать быстроту изменения величины скорости.Составляющая же, направленная по нормали к траектории и называемая нормальным (или центростремительным) ускорением, будет характеризовать быстроту изменения скорости только по направлению. Найдем эти составляющие ускорения.С этой целью удобнее всего использовать так называемый «естественный» способ описания движения точки, который применяют тогда, когда заранее известна траектория точки.Положение точки определяют дуговой координатой – расстоянием вдоль траектории от выбранного начала отсчета .При этом произвольно устанавливают положительное направление отсчета координаты (например, так, как показано стрелкой).Движение точки определено, если известны ее траектория, начало отсчета , положительное направление дуговой координаты и закон движения точки, то есть зависимость .Найдем скорость производной точки твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью . Пусть положение точки относительно некоторой точки оси вращение характеризуется радиус-вектором (рис. 2.4.).

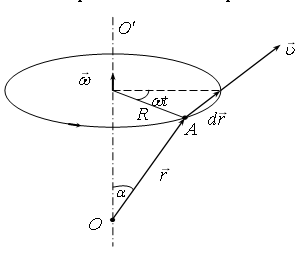
Записав и поделив ее на соответствующий промежуток времени , получим ; , то то есть скорость любой точки твердого тела, вращающегося вокруг некоторой оси с угловой скоростью , равна векторному произведению на радиус-вектор точки относительно произвольной точки оси вращения.Модуль вектора где – радиус окружности, по которой движется точка . Продифференцировав по времени, найдем полное ускорение точки : .

В данном случае (ось вращения неподвижна) , поэтому вектор представляет собой тангенциальное ускорение . Вектор же – нормальное . Модули этих ускорений

Отсюда модуль полного ускорения

9 Момент импульса частицы относительно точки и оси.

Кроме импульса существует еще одна механическая величина, с которой так же связан закон сохранения, – это так называемый момент импульса.

Сначала возьмем одну частицу (рис. 5.1). Пусть – радиус-вектор, характеризующий положение частицы А относительно некоторой точки О выбранной системы отсчета, а – ее импульс в этой системе.

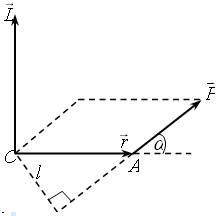
следует, что является аксиальным вектором. Его направление выбрано так, что вращение вокруг точки О в направлении вектора и вектор образуют правовинтовую систему. Вектор перпендикулярен к плоскости векторов и , и если смотреть вслед вектору , то совершаемый по кратчайшему пути поворот от к осуществляется по часовой стрелке. Модуль вектора равен:

где – угол между и ; – плечо вектора относительно точки О.