34. Магнитное поле прямолинейного проводника с током.
Применим
формулу (23.1)
для вычисления поля прямого тока, т.е.
поля, создаваемого током, текущим по
тонкому прямому проводу конечной длины
(рис. 23.2). Все векторы
в данной точке А
имеют одинаковое направление (в нашем
случае за чертеж). Поэтому сложение
векторов
можно заменить сложением их модулей.
Точка, для которой мы вычисляем магнитную
индукцию, находится на расстоянии b
от провода.
Из рисунка 23.2 видно, что
.
Подставим
эти значения в формулу (23.2)
Формула
(23.9) записана для вакуума (
).
Угол
для всех элементов проводника конечной
длины между точками 1 и 2 изменяется в
пределах от
до
.
Чтобы определить магнитную индукцию
поля, создаваемого отрезком проводника,
проинтегрируем выражение (23.9) в пределах
от
до
:
.
(23.10)
Заметим,
что при симметричном расположении точки
А
относительно отрезка провода
.
С учетом этого формула (23.10) прямой вид:
.
(23.11)
Если
длина l проводника с током намного больше
расстояния b,
то
,
и для такого бесконечно
длинного
проводника получим:
.
(23.12)
Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 23.3).
35 Магнитное поле кругового проводника с током.
Рассмотрим
поле, создаваемое током, текущим по
тонкому проводу, имеющему форму окружности
радиуса R
(круговой ток). Определим магнитную
индукцию в центре кругового тока
(рис.23.4). каждый элемент тока создает в
центре индукцию, направленную вдоль
положительной нормали к контуру. Поэтому
векторное сложение
сводится к сложению их модулей. По
формуле (23.2)
(
).
Проинтегрируем это выражение по всему
контуру:
.
Выражение
в скобках равно модулю дипольного
магнитного момента
(см.(22.6)).
Следовательно, магнитная индукция в
центре кругового тока имеет величину
.
(23.13)
Из
рис. 23.4 видно, что направление вектора
совпадает с направлением положительной
нормали к контуру, т.е. с направлением
вектора
.
Поэтому формулу (2.13) можно написать в
векторном виде:
.
(23.14)
Теперь найдем на оси кругового тока на расстоянии h от центра контура (рис. 23.5).
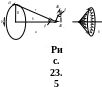
Векторы
перпендикулярны
к плоскостям, проходящим через
соответствующий элемент
и точку, в которой мы ищем поле.
Следовательно, они образуют симметричный
конический веер (рис. 23.5, б). Из соображений
симметрии можно заключить, что
результирующий вектор
направлен вдоль оси контура. Каждый из
составляющих векторов
вносит в результирующий вектор вклад
,
равный по модулю
.
Угол
между
и
прямой, поэтому
.
Проинтегрировав
по всему контуру и заменив r
на
, получим
(23.15)
Эта формула определяет величину магнитной индукции на оси кругового тока. Приняв во внимание, что векторы и имеют одинаковое направление, можно написать формулу (2.15) в векторном виде:
.
(23.16)
Это выражение не зависит от знака r. Следовательно, в точках оси, симметричных относительно центра тока, имеет одинаковую величину и направление.
При h = 0 формула (23.16) переходит, как и должно быть, в формулу (23.14) для магнитной индукции в центре кругового тока.
На
больших расстояниях от контура в
знаменателе можно пренебречь
по сравнению с
.
Тогда формула (23.16) принимает вид
(на
оси тока). (23.17)