41 Закон Ома для однородного проводника. Закон Ома в дифференциальной форме.

Рассмотрим цепь, состоящую из внешнего сопротивления R и источника тока с ЭДС и внутренним сопротивлением r (рис.20.2).

Р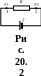 абота по перемещению заряда по замкнутому контуру равна:

. (20.12)

Работа по перемещению заряда из точки 1 в точку 2 ( ) совершается кулоновскими силами и будет равна:

.

Перемещение заряда из точки 2 в точку 1 осуществляется сторонними силами (источником тока)

Подставляя выражения А₁₂ и А₂₁ в формулу(20.12), получим:

(20.13)

Отношение работы по перемещению заряда по замкнутому контуру к величине переносимого заряда, называется напряжением U. Следовательно,

(20.14)

Участок цепи, в котором отсутствует ЭДС, называется однородным.

Для такого участка цепи и называется падением напряжения на данном участке цепи. Сила тока на этом участке цепи:

(20.15)

«закон Ома¹ для однородного участка цепи в интегральной форме», где R – сопротивление проводника .

Для неоднородного участка цепи ( ) закон Ома можно записать в виде: , (20.16)

где R_общ. – общее сопротивление цепи. Если , то: , (20.17)

где R_внеш. – сопротивление внешнего участка цепи, r – внутреннее сопротивление батареи.

Если R_внеш = 0, то в цепи возникает достаточно большой величины ток короткого замыкания (КЗ):

. (20.18)

Для вывода закона Ома в дифференциальной форме выделим бесконечно малый элемент проводника длиной dl и площадью сечения проводника ds. Падение напряжения на выделенном элементе проводника , сила тока , а сопротивление проводника .

Тогда выражение (20.15) для выделенного элемента проводника можно записать в виде: ,

откуда:

, (20.19)

где  – удельное сопротивление проводника, _уд. – удельная электропроводность ( ).

Так как напряженность поля и плотность тока – величины векторные, то выражение (20.19) можно записать:

(20.20)

«закон Ома в дифференциальной форме», т.е. вектор плотности тока пропорционален напряженности электрического поля. Коэффициентом пропорциональности является удельная электропроводность _.

Для неоднородного участка цепи закон Ома в дифференциальной форме имеет вид:

(20.21)

где – напряженность поля сторонних сил (э.д.с. источника).

42. Ток смещения

Со­гласно теореме о цирку­ляции вектора Н: (1)

Применим эту тео­рему к случаю, когда предварительно заря­женный плоский

конденсатор разряжается через некото­рое внешнее сопротивление. В качестве кон­тура Г возьмем кривую, охватывающую провод.

На кон­тур Г можно натянуть разные поверхности, например S и S'. Через поверхность S течет ток I, а через поверхность S' – нет. Получается, что циркуляция вектора Н зависит оттого, какую поверхность мы натягиваем на данный контур, чего явно не может быть. Поверхность S' «пронизывает» только электрическое поле. По теореме Гаусса поток вектора D сквозь замкнутую поверхность ∫DdS=q, откуда:

С другой стороны, согласно уравнению непрерывности:

Сложив отдельно левые и правые части уравнений, получим (4):

Это уравнение аналогично уравнению непрерывности для постоянного тока. Из него видно, что кроме плотности тока проводимости j имеется еще одно слагаемое дD/дt, раз­мерность которого равна размерности плотности тока. Это – плотность тока смещения: j_см = дD/дt. Сумму же тока проводимости и тока смещения называют полным током. Его плотность j_полн=j+дD/дt. Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения. Введение полного тока устраняет трудность, связанную с зависимостью циркуляции вектора Н от выбора поверхности, натягиваемой на контур Г. Для этого достаточно в правой части (1) вместо тока проводимости ввести полный ток, т. е. величину I_полн=∫(j+ дD/дt)dS. В самом деле, правая часть этого ур–ия представляет собой сумму тока проводимости I и тока смещения I_см: I_полн=I+I_см. Покажем, что полный ток I_полн будет одинаков и для поверхности S, и для поверхности S', натянутых на один и тот же контур Г. Для этого применим (4) к замк­нутой поверхности, составленной из поверхностей S и S'. Учитывая, что для замкнутой поверхности нормаль n направлена наружу:

I_полн(S')+I_полн(S)=0. Теперь, если обернуть нормаль n' для поверхности S' в ту же сторону, что и для S, то первое слагаемое в послед­нем уравнении изменит знак, и получим:

I_полн(S') =I_полн(S), что и требовалось доказать.

Итак, теорему о циркуляции вектора Н можно обобщить для произвольного случая:

В таком виде теорема о циркуляции вектора Н справедлива всегда.