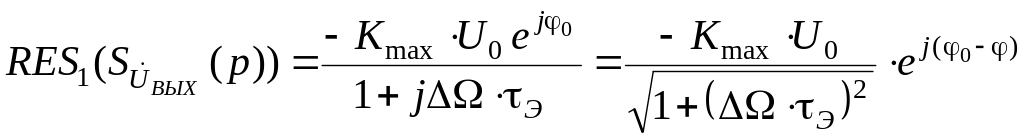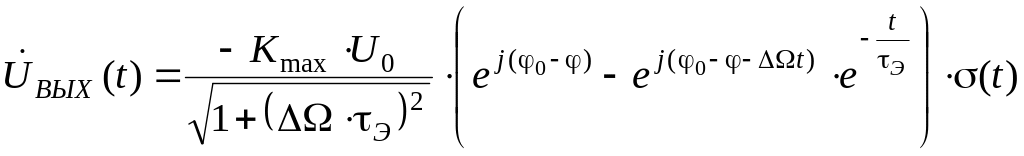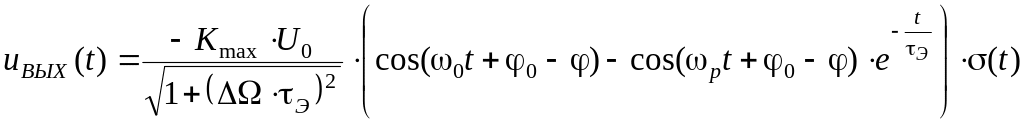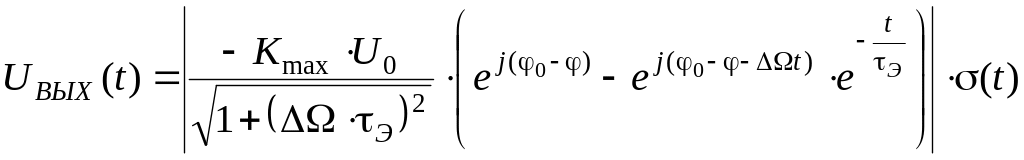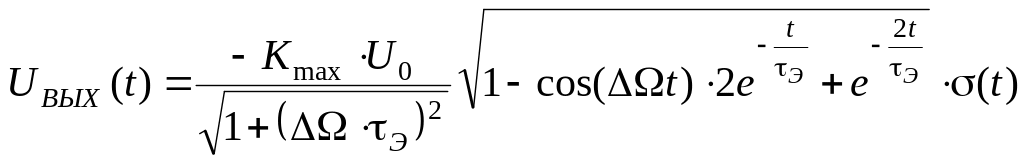2.2.4Спектральный метод огибающей

Исходной информацией анализа узкополосного сигнала является его спектральная плотность и АЧХ избирательной цепи. На рисунке 2.1 изображен амплитудный спектр сигнала и АЧХ.

Спектральная плотность узкополосного входного колебания имеет два всплеска вблизи частот + ω₀ и – ω₀. Частотный коэффициент передачи избирательной цепи также имеет два всплеска, но вблизи частот + ω_р и – ω_р. В общем случае несущая частота ω₀ и ω_р не совпадают, т. к. существует расстройка:

(2.26)

Расстройка является величиной того же порядка, что и полоса пропускания цепи (на рисунке расстройка показана больше по величине). Спектральная плотность аналитического сигнала равна нулю в области отрицательных частот, и удвоенной спектральной плотности входного сигнала в области положительных частот.

Рис. 2.1 Спектр входного сигнала , спектр аналитического сигнала

и АЧХ резонансного усилителя

Спектральная плотность аналитического сигнала, сдвинутая на величину ω₀ влево, совпадает со спектральной плотностью комплексной огибающей. В новой системе координат текущей является частота .

Частотный коэффициент передачи тоже сдвигается на ω₀ и переходит в частотный коэффициент передачи эквивалентной низкочастотной цепи .

Таким образом, от радиосигнала и высокочастотной цепи осуществляется переход к видеосигналу и низкочастотной цепи. Спектральная плотность комплексной огибающей выходного сигнала будет равна:

,

(2.27)

Выражение (2.27) определяет спектральный метод огибающей. Это же выражение в форме преобразования Лапласа определяет операторный метод огибающей.

Рис. 2.2 Спектр огибающей и АЧХ эквивалентной низкочастотной цепи резонансного усилителя

,

(2.27)

Использование метода огибающей позволяет сократить число особых точек, а значит, и число вычетов в два раза по сравнению с обычным спектральным (операторным) методом.

2.2.5Временной метод огибающей

Импульсная характеристика избирательной цепи также может быть представлена в виде квазигармонического колебания:

(2.28)

где – комплексная огибающая импульсной характеристики.

Выходной сигнал может быть найден с помощью интеграла Дюамеля, связывающего комплексную огибающую выходного сигнала с комплексной огибающей входного сигнала и импульсной характеристикой цепи:

(2.29)

где – комплексная огибающая импульсной характеристики, со сдвинутым спектром.

2.3Прохождение радиоимпульса с прямоугольной огибающей через резонансный усилитель

2.3.1Воздействие на резонансный усилитель радиоимпульса включения

Радиоимпульс включения описывается выражением:

(2.30)

Комплексная огибающая входного сигнала будет равна:

(2.31)

Изображение комплексной огибающей входного сигнала по Лапласу:

(2.32)

Частотный коэффициент передачи:

(2.33)

Коэффициент передачи эквивалентной низкочастотной цепи:

(2.34)

Изображение комплексной огибающей выходного сигнала:

(2.35)

Комплексная огибающая выходного сигнала может быть найдена через вычисление вычетов:

(2.36)

(2.37)

(2.38)

где – фаза знаменателя.

(2.39)

(2.40)

(2.41)

Комплексная огибающая выходного сигнала:

(2.42)

(2.43)

Выходной сигнал:

(2.44)

(2.45)

(2.46)

Таким образом, при подаче в момент времени t = 0 на вход резонансного усилителя гармонического колебания, на выходе будет сигнал, содержащий две составляющие: первая – это стационарное колебание с частотой входного сигнала и вторая – свободные затухающие колебания с частотой , последняя при высокой добротности контура очень мало отличается от резонансной частоты .

Если расстройка , то выходной сигнал будет содержать колебания только с частотой :

(2.47)

Физическая огибающая выходного сигнала будет нарастать по экспоненциальному закону, скорость нарастания огибающей определяется постоянной времени , максимальное значение огибающей равно .

Если расстройка будет отлична от нуля, огибающая выходного сигнала будет иметь более сложный характер:

(2.48)

(2.49)

(2.50)

(2.51)

Графики физической огибающей приведены на рисунке 2.3. При нулевой расстройке процесс установления выходного напряжения носит аппериодический характер, при увеличении расстройки сначала появляется превышение огибающей установившегося значения, а затем процесс установления носит колебательный характер. Объясняется это тем, что в системе присутствуют два колебания с близкими частотами ω₀ и ω_р. Взаимодействие этих колебаний характеризуется изменением амплитуды. С увеличением расстройки крутизна фронта огибающей растет. Это приводит к уменьшению времени переходного процесса. Одновременно с этим при увеличении расстройки происходит уменьшение амплитуды выходного сигнала.

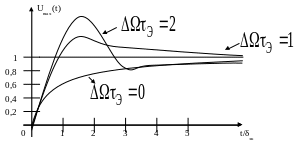
Рис. 2.3 Физическая огибающая выходного сигнала резонансного усилителя

при воздействии радиоимпульса включения

Если длительность импульса Т больше фактического времени установления режима в контуре при включении гармонической ЭДС, то к моменту окончания входного импульса на выходе усилителя амплитуда колебания будет равна стационарному значению:

(2.52)