5.3Воздействие случайных сигналов на нелинейную цепь

Реальная нелинейная цепь представляет собой сочетание нелинейных безынерционных элементов с линейными инерционными цепями.

При воздействии случайного сигнала на нелинейный элемент достаточно просто определяется закон распространения выходного сигнала, а задача нахождения спектральной плотности мощности и корреляционной функции выходного сигнала является весьма сложной. При воздействии случайного сигнала на линейную цепь достаточно просто находится спектральная плотность мощности и корреляционная функция.

А задача нахождения закона распространения выходного сигнала является сложной.

В настоящее время общих методов анализа воздействия случайных колебаний на нелинейные цепи не существует и решены только отдельные практические задачи.

Рассмотрим методику определения закона распределения сигнала на выходе нелинейного элемента в случае, когда известны закон распределения входного сигнала и функциональная связь между выходным и входным сигналом.

Дано:

y = f(x), P_вх(x)

Определить: P_вых(y)

Тогда вероятность попадания входного сигнала на интервал (х; х + dx) будет равна вероятности попадания выходного сигнала на интервал (y; y + dy)

Если функциональная зависимость y = f(x) – убывающая, то , а плотности вероятности отрицательная быть не может, поэтому производную берут по модулю. Если обратная функция является неоднозначной, то обратная функция :

В этом случае находится плотность вероятности для каждой ветви обратной функции, а затем результаты суммируются:

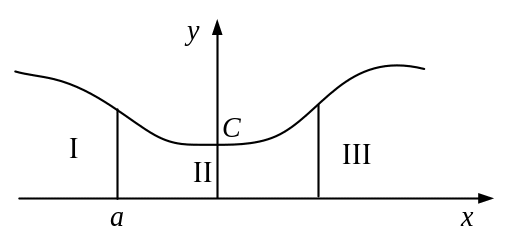
Если на некотором интервале изменение входного сигнала является постоянным, то выходная плотность вероятности будет совершать -функцию отличную от нуля при значении равном значению выходного сигнала, а площадь под этой -функцией определяется вероятностью попадания входного сигнала на рассматриваемый интервал:

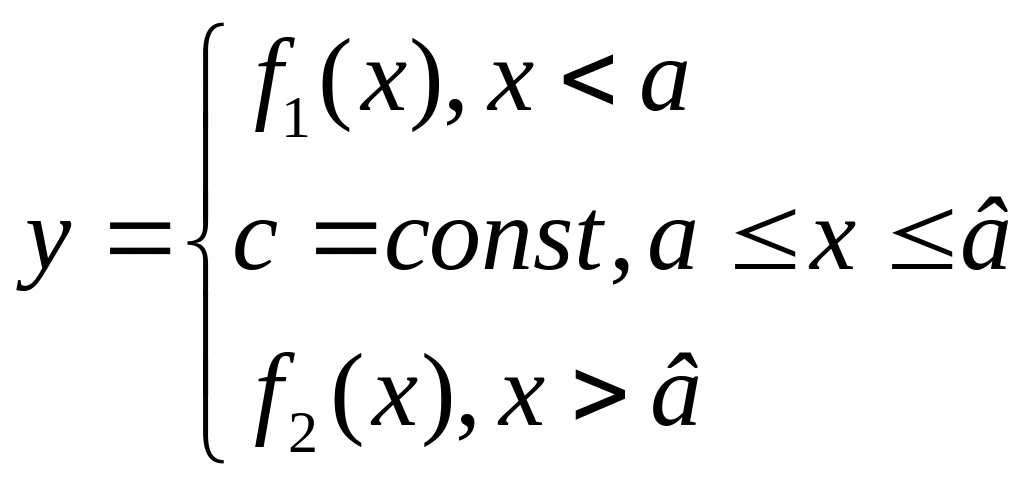
где

Необходимо учитывать условие калибровки:

Пример

На выходе:

1.

2.

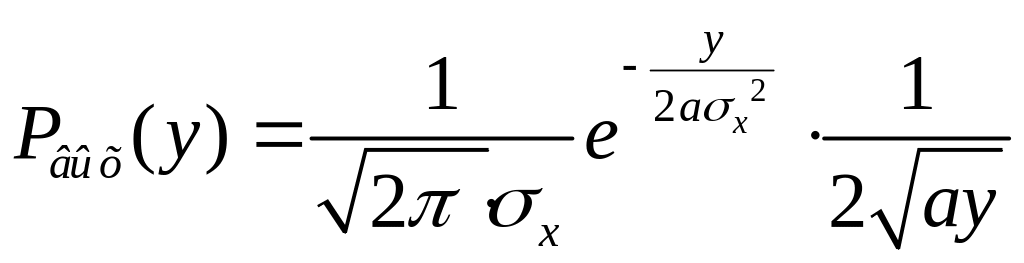y ≥ 0

6Параметрические цепи

Электрические цепи в которых хотя бы один из параметров изменяется по заданному закону во времени называется цепью с переменными параметрами или параметрической цепью.

Рассмотрим линейный параметрический резистивный элемент и параметрический ёмкостной элемент.

6.1Параметрический резистивный элемент

Он хорошо реализуется на базе нелинейного элемента. Допустим имеется нелинейный элемент на вход которого подаётся управляющее U_y и сигнальное U_c напряжения. Управляющее напряжение много больше сигнального.

Ток, протекающий через нелинейный элемент, можно разложить в ряд Тейлора:

При малых амплитудах сигнала слагаемыми и степенями «2» и выше можно пренебречь, поэтому:

Полезная составляющая выходного тока, которая вызывается наличием входного сигнала:

т. е. – диффузионная крутизна ВАХ при заданном управляемом сигнале.

Такой элемент оказывает сопротивление току:

Используя такой элемент можно реализовать преобразователь частоты.

Гетеродин представляет собой генератор гармонического сигнала с постоянной амплитудой. Т. е. управляющее напряжение (U_г) является периодическим, поэтому диффузионная крутизна (S_диф) изменяется во времени по периодическому закону.

S_диф может быть представлена рядом Фурье:

где

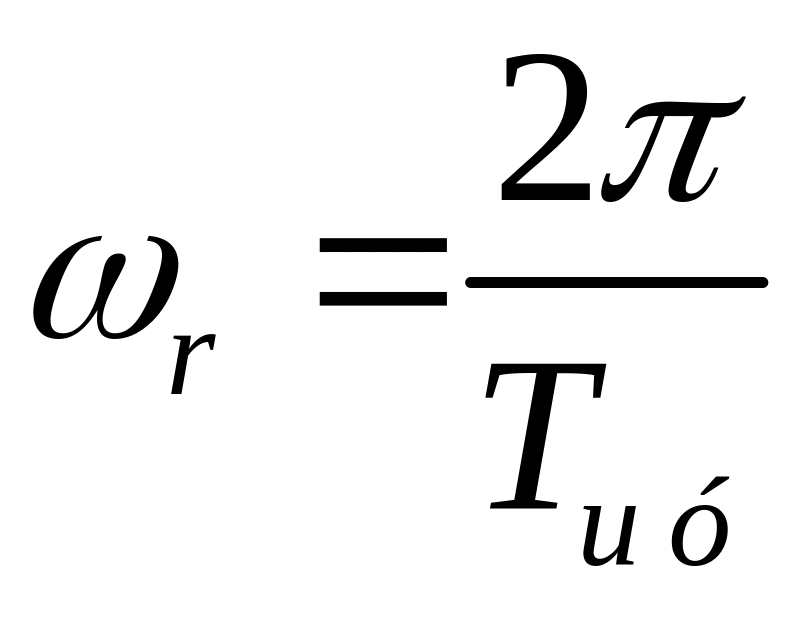
Допустим, что на вход смесителя поступает сигнал с тональной АМ:

тогда

Если в качестве фильтра взять контур настроенный на промежуточную частоту и имеющий , то на входе контура:

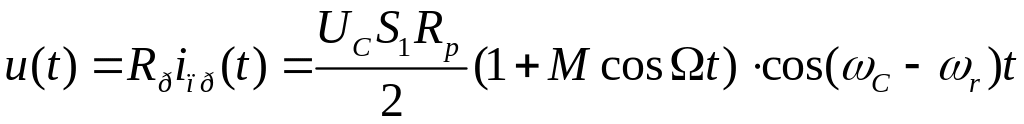
Таким образом, входное напряжение на промежуточной частоте имеет тот же закон модуляции, что и входное напряжение. Такой преобразователь частоты называют линейным. Следует заметить, что описанный преобразователь частоты реагирует одинокого на сигналы с частотами:

Преобразователь частоты не фильтрует сигнал зеркального канала и последний оказывает мешающее действие. Для нормальной работы зеркальный канал должен быть подавлен до гетеродина (его частоты).

Для этого перед преобразователем частоты сигнал зеркального канала подавляется во входной цепи приёмника и усилителя высокой частоты.

Для характеристики работы преобразователя используют понятие крутизны преобразования. Оценивая её как отношение амплитуды тока на частоте преобразования к амплитуде немодулированного входного сигнала:

Таким образом крутизна преобразования равна половине амплитуды первой гармоники диффузионной крутизны.

Например, элемент имеет , а

Тогда диффузионная крутизна:

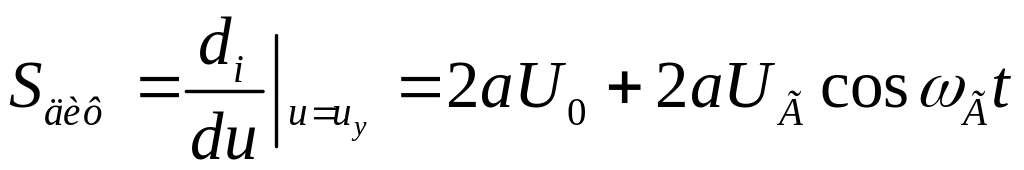
Отсюда:

Таким образом, крутизна преобразования пропорциональна амплитуде напряжения гетеродина.