5.5Умножение частоты

В нелинейном усилителе коллекторный ток наряду с основной гармоникой, имеющей частоту ω_вх содержит гармоники с кратными частотами kω_вх, k = 2,3, … Это может быть использовано для умножения частоты. Частота выходного сигнала будет в k – раз превышать частоту входного сигнала, если контур в цепи коллектора настроить на частоту kω_вх.

Схема замещения умножителя частоты аналогична схеме замещения усилителя, отличие состоит в том, что S_ср приведённая к k – ой гармонике будет вычисляться так:

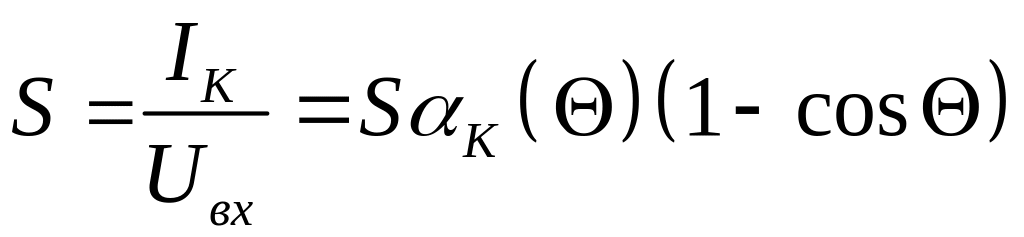
и сопротивление:

Оптимальный угол отсечки равен . Для получения максимальной мощности выходного сигнала необходимо поддерживать амплитуду импульса коллекторного тока постоянной, для этого наряду с увеличением напряжения смещения приходится повышать амплитуду входного сигнала.

Такой подход приводит к ухудшению энергетических соотношений в умножителе. С учётом этого в одном каскаде обычно применяют удвоение, реже утроение частоты.

5.6Преобразование частоты сигнала

Под преобразованием частоты понимают сдвиг спектра сигнала по оси частот на определенный интервал при сохранении структуры спектра.

Любой супергетерадинный приемник использует операцию преобразования частот для переноса спектра сигнала с частоты принимаемой радиостанции на промежуточную частоту f_пр = 465 кГц.

Основное усиление сигнала ведется на промежуточной частоте.

Рассмотрим суть преобразования частоты. Допустим, на нелинейный элемент действуют два сигнала (колебания):

1. информационный сигнал

2. вспомогательный сигнал от специального генератора, называемого гетеродином (параметры неизменны во времени)

Для преобразования частоты используется нелинейный элемент, и задача преобразования состоит в получении сигнала с частотой, равной сумме или разности сигнала и гетеродина .

Для получения такой комбинационной частоты степенной полином, аппроксимирующий ВАХ, должен содержать член четвертой степени. Допустим, что ВАХ нелинейного элемента описывается полиномом четвертой степени:

Из множества слагаемых в формировании промежуточной частоты будут принимать участие только следующие слагаемые:

­- слагаемое с частотой .

Таким образом, в спектре тока будет присутствовать составляющая

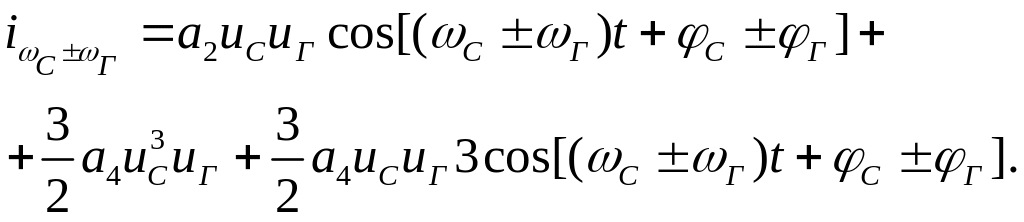
Если в спектре нагрузки использовать фильтр, настроенный на частоту , то напряжение на выходе преобразователя будет иметь следующий вид:

Из последнего выражения видно, что законы изменения частоты и фазы при преобразовании частоты не изменяются. Для того чтобы сохранялся закон изменения амплитуды, необходимо потребовать выполнение следующего неравенства:

.

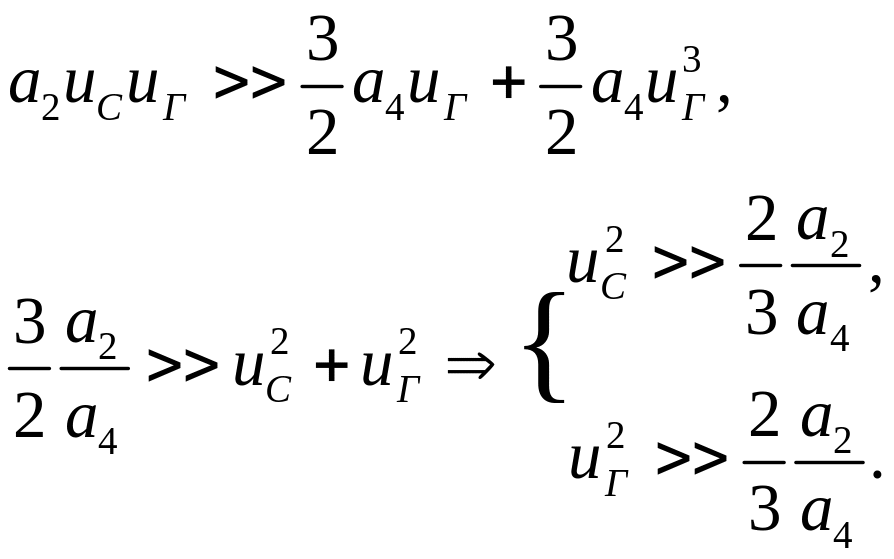
Для реализации преобразования частоты можно использовать различные нелинейные элементы.

При выделении разностной частоты необходимо помнить, что структура спектра сохраняется, если (1). Если (2), то спектр переворачивается (или отражается зеркалом).

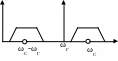
Такое изменение спектра необходимо учитывать в том случае, когда сигнал имеет спектр, несимметричный относительно центральной частоты.