
- •Тема1.1 Информация, количество информации
- •1.1.1. Данные и информация
- •Виды информации
- •Действия над информацией
- •Свойства информации
- •Передача информации
- •Тема1.2 Системы счисления и область их использования
- •Любое число может быть представлено последовательностью двоичных цифр
- •Восьмеричная система счисления
- •Шестнадцатеричная система счисления
- •Сводная таблица переводов целых чисел из одной системы счисления в другую
- •Сводная таблица переводов целых чисел
- •Арифметические операции в позиционных системах счисления
- •Тема1.3 Кодирование информации
- •Формула Хартли
- •Кодирование чисел
- •Раздел II текстовые процессоры Тема 2.1. Текстовые редакторы и текстовые процессоры
- •I. Текстовые редакторы и текстовые процессоры, их возможности
- •II. Текстовый процессор Word, основные элементы экрана
- •Кнопки перехода Полосы прокруток Панель инструментов Рисование Строка состояния
- •IV. Редактирование документа
- •V. Форматирование документов
- •Тема 2.2. Форматирование страниц
- •I. Изменение формата листа
- •Установка полей.
- •Изменение размера бумаги.
- •II. Режимы работы в Word
- •Обычный режим
- •Режим разметки страниц
- •Режим просмотра перед печатью
- •Режим электронного документа
- •Режим структуры документа
- •Создание сложного документа
- •III. Колонтитулы
- •IV. Сноски.
- •V. Оглавления.
- •VI. Средства поиска и замены
- •VII. Проверка правописания
- •Тема 2.3. Создание и форматирование таблиц.
- •I. Создание таблиц
- •II. Создание таблиц
- •III. Форматирование таблиц
- •Тема 2.4. Основные приемы оформления текста в колонки.
- •I. Оформление текста в колонки
- •II. Табуляция
- •Тема 2.5. Графические возможности Word
- •I. Вставка в текст символов
- •II. Вставка и редактирование готовых графических объектов
- •Редактирование графических объектов
- •Группировка графических объектов
- •III. Вставка в текст создаваемого рисунка
- •IV. Вставка в текст надписей и автофигур
- •V. Интеграция ole – объектов в wor
- •Приложение ms Equation Editor
- •Приложение Microsoft WordArt
- •Тема 3.1. Электронные таблицы Excel
- •I. Электронные таблицы Excel
- •Окно программы Excel, меню программы, панель окна Excel.
- •II. Редактирование таблиц
- •Копирование диапазона ячеек
- •III. Форматирование таблиц
- •Изменение ширины столбцов
- •V. Ввод данных в ячейки, типы данных.
- •VII. Относительная и Абсолютная адресация ячеек Относительная адресация
- •Абсолютная адресация
- •Тема 3.2. Использование формул. Мастер функций.
- •I. Формулы и функции.
- •II. Мастер функций
- •III. Автосуммирование.
- •IV. Логические функции
- •В ответе получаем 3.
- •V. Работа с несколькими листами, ссылки на другие листы.
- •Тема 3.3. Графическое отображение данных. Мастер диаграмм.
- •I. Графическое отображение данных
- •II. Создание диаграммы
- •III. Форматирование диаграмм Изменение диапазона ячеек, используемого для создания диаграммы
- •Задание текста вдоль горизонтальной оси
- •Диаграмма не измеряет и не выводит на экран данные требуемым образом
- •Изменение типа диаграммы
- •IV. Примеры выделения и построения диаграмм
- •V. Связь программ Word и Excel. Импорт и экспорт документов.
- •Тема 3.4. Сортировка и поиск информации в электронной таблице.
- •I. Создание и редактирование списков
- •II. Сортировка записей в списке
- •III. Отбор записей
- •IV. Способы отбора
- •V. Расширенный фильтр
- •Тема 4. Автоматизация документооборота.
- •I. Системы автоматизации документооборота:
- •II. Сканирование и распознавание документа
- •III. Основные методы сканирования документа
- •IV. Системы автоматизированного перевода документов
- •Тема 5. Компьютерная графика.
- •I.Компьютерная графика, основные понятия
- •II. Методы представления графических изображений
- •III. Растровая графика
- •IV. Векторная графика
- •V. Цветовое разрешение и цветовые модели
- •VI Обзор современных пакетов для обработки компьютерной графики
- •VII. Форматы графических файлов
- •Тема 6.1. Базы данных.Основные понятия.
- •II. Системы управления базами данных
- •Возможность внесения и чтения информации.
- •Возможность работы с большими объемами данных.
- •Скорость поиска.
- •Целостность данных.
- •Защита данных из базы от разрушения.
- •Защита данных от несанкционированного доступа.
- •III. Структура базы данных
- •IV. Виды моделей баз данных
- •Тема 6.2. Субд Ms Access.
- •I. Свойства полей. Типы полей
- •II. Субд Access – общие моменты
- •III. Таблицы. Создание таблиц
- •IV. Запросы
- •V. Формы
- •VI. Отчеты
- •Тема 7. Автоматизированные информационные системы
- •I. Понятие информационной системы
- •II. Классификации ис
- •III. Автоматизированные информационные системы
- •Создание и улучшение продукции.
- •IV. Системы автоматизированного проектирования сапр
- •V. Автоматизированные системы научных исследований
- •VI. Геоинформационные системы
- •Тема 8. Экспертные системы
- •I. Понятие экспертной системы
- •II. Структура эс
- •III. Процесс разработки эс
Любое число может быть представлено последовательностью двоичных цифр
an an-1 an-2 . . . a1 a0 , a-1 a-2 . . . a-k, где ai либо 0, либо 1.
Эта запись соответствует сумме степеней числа 2, взятых с указанными в ней коэффициентами (полином):
an * 2n + an-1* 2n-1 + an-2 * 2n-2 + ...+ a1 * 21 + a0* 20 + + a-1* 2-1 + a-2 * 2-2 +...+ a-k * 2-k
Например:
Двоичное число
(10101101,101)2= 1* 27 + 0* 26 + 1* 25 + 0* 24 +1* 23+1*22+0*21 +1*20 + 1*2-1+0*2-2 +1*2-3
что соответствует десятичному числу 173,62510
Преимущества двоичной системы
Двоичное изображение числа требует большего количества разрядов, чем его десятичное представление. Тем не менее, применение двоичной системы удобно тем, что для представления в вычислительной технике двоичного числа может быть использован любой простой элемент, имеющий всего два устойчивых состояния.
Другим важным достоинством двоичной системы является простота двоичных арифметических действий.
Восьмеричная система счисления
В восьмеричной системе употребляются восемь цифр: 0,1,2, 3, 4, 5, 6, 7.
Любое число в восьмеричной системе представляется последовательностью цифр
bn bn-1 bn-2 . . . b1 b0 , b-1 b-2 . . . b-k ,в которой b могут принимать значения: 0, 1, 2, 3, 4, 5, 6, 7.
Этой записи соответствует разложение числа по степеням числа 8:
bn * 8n + bn-1* 8n-1 + bn-2 * 8n-2 + ...+ b1 * 81 + b0* 80 + b-1* 8-1 + b-2 * 8-2 +...+ b-k * 8-k
Пример
восьмеричное число (703,04)8= 7*82 +0*81+3*80+0*8-1+4*8-2 = (451,0625)10
Восьмеричная система используется для компактной записи двоичных команд и чисел.
Преимущества восьмеричной системы
Простота перевода в двоичную систему счисления.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления для изображения чисел употребляется 16 цифр. При этом, чтобы одну цифру не изображать двумя знаками, приходится вводить специальные обозначения для цифр, больших 9. Первые десять цифр этой системы обозначаются цифрами 0, 1,2, 3, 4, 5, 6, 7, 8, 9, а старшие шесть цифр этой системы - латинскими буквами: десять-А, одиннадцать-В, двенадцать-С, тринадцать-D, четырнадцать-Е, пятнадцать-F.
Произвольное число в шестнадцатеричной системе может быть записано в виде последовательности цифр: сn сn-1 сn-2 . . . с1 с0 , с-1 с-2 . . . с-k , где с может принимать любые из шестнадцати значений: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Этой записи соответствует разложение числа по степеням числа 16:
сn *16n + сn-1*16n-1 + сn-2 *16n-2 + ...+ с1 *161 + с0*160 + с-1*16-1 + с-2 *16-2 +...+ с-k *16-k
Пример
шестнадцатеричное число (В2Е.4)16 =11*162+2*161+14*160+4*16-1 = 2862,2510
Преимущества 16-тиричной системы
Шестнадцатеричная система позволяет записывать коды и команды еще более компактно.
Таблица соответствия первых 10-ти чисел в различных системах счисления
10 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
2 |
0 |
1 |
01 |
11 |
100 |
101 |
110 |
111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
10000 |
8 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
20 |
16 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
А |
B |
C |
D |
E |
F |
10 |
Перевод чисел из одной системы счисления в другую и обратно
Перевод целого числа из десятичной системы счисления в любую другую позиционную систему счисления
Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
![]()
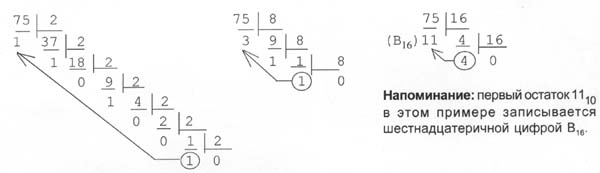
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Перевод числа из двоичной, восьмеричной, шестнадцатеричной системы счисления в десятичную
Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q сводится к вычислению многочлена
x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-mq-
средствами десятичной арифметики
Примеры

