
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
§ 2.4. Базис векторного пространства. Координаты вектора
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано для строк матрицы.
Определение.
Линейной
комбинацией
векторов
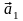 ,
,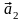 ,...,
,...,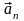 с коэффициентами C1,C2,...,Cn
называется вектор C1
+C2
+...+Cn
с коэффициентами C1,C2,...,Cn
называется вектор C1
+C2
+...+Cn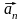 .
.
Эта комбинация обладает двумя основными свойствами.
Если векторы , ,..., коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой.
Векторы , ,..., называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если векторы , ,..., компланарны некоторой плоскости, то любая их линейная комбинация компланарна той же плоскости.
Определение. Векторы , ,..., называются линейно зависимыми, если существуют такие числа C1,C2,...,Cn , не все равные нулю, что C1 +C2 +...+Cn =0
В противном случае векторы , ,..., называются линейно независимыми.
Определение. Совокупность n линейно независимых векторов называется базисом.
Множество всех плоских или пространственных векторов в которых определены операции сложения векторов и умножение вектора на число, являются простейшими примерами векторного пространства.
Определение. Множество векторов, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше семи свойствам называется векторным пространством.
Оказывается, что в любом векторном пространстве всегда можно выбрать несколько векторов, из которых с помощью линейных комбинаций однозначно можно получить любой вектор этого пространства и которые являются базисными.
Определение.
Любой ненулевой
вектор
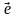 на прямой называется
на прямой называется
базисным
вектором
этой
прямой.
Любая пара неколлинеарных векторов
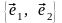 плоскости называется
базисом этой плоскости.
Любая тройка некомпланарных векторов
плоскости называется
базисом этой плоскости.
Любая тройка некомпланарных векторов
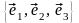 называется
базисом пространства.
называется
базисом пространства.
Теорема о базисе.Любой вектор (на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,
на прямой:
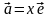
на плоскости:
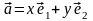
в пространстве:
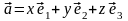
Доказательство.
Случай прямой.
Пусть вектор
лежит на прямой L,
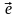 –
базисный вектор этой прямой. Отложим
вектора
и
из некоторой точки O
на прямой, вектор
возьмём в качестве масштабного единичного
отрезка на L,
в результате на L
образуется координатная ось. Пусть
конец вектора
есть точка A,
и x
её координата на этой оси, тогда согласно
определению произведения вектора на
число имеем
–
базисный вектор этой прямой. Отложим
вектора
и
из некоторой точки O
на прямой, вектор
возьмём в качестве масштабного единичного
отрезка на L,
в результате на L
образуется координатная ось. Пусть
конец вектора
есть точка A,
и x
её координата на этой оси, тогда согласно
определению произведения вектора на
число имеем
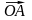 =x
,
т.е.
=x
.
=x
,
т.е.
=x
.
L

Случай плоскости.
Пусть векторы
,
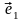 и
и
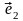 лежат в плоскости
лежат в плоскости
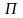 .Отложим
их из некоторой точки O
этой плоскости, конец вектора
обозначим через A.
.Отложим
их из некоторой точки O
этой плоскости, конец вектора
обозначим через A.
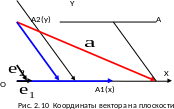
Проведём через вектора и оси Ox и Oy с единичными отрезками
и , через точку A проведём прямые параллельные этим осям, их точки пересечения с OX и Oy обозначим через A1 и A2 соответственно.
П
Координату точки
A1
на Ox
обозначим через x,
а координату точки A2
на Oy
– через y.
Тогда
используя определение суммы векторов
и предыдущий случай
получим:
=
=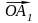 +
+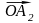 =x
+y
.
=x
+y
.
3)
Случай пространства. Отложим вектора
,
 ,
,
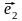 и
и
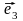 из некоторой точки O,
через вектора
,
,
и
из некоторой точки O,
через вектора
,
,
и
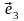 проведём оси Ox,
Oy,
Oz.
Из конца вектора
,
точки A
проведём три плоскости, параллельные
парам осей Ox,
Oy;
Oy,
Oz
и Ox,
Oz.
Их точки пересечения с осями Ox,
Oy,
Oz
обозначим через A1,
A2,
A3,
а координаты этих точек на осях через
x,
y,
z.
В результате мы имеем.
=
=
+
+
проведём оси Ox,
Oy,
Oz.
Из конца вектора
,
точки A
проведём три плоскости, параллельные
парам осей Ox,
Oy;
Oy,
Oz
и Ox,
Oz.
Их точки пересечения с осями Ox,
Oy,
Oz
обозначим через A1,
A2,
A3,
а координаты этих точек на осях через
x,
y,
z.
В результате мы имеем.
=
=
+
+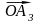 =x
+y
+z
.
=x
+y
+z
.

Проверим, что коэффициенты (x, y, z) линейной комбинации определяется однозначно. Допустим противное, пусть вектор можно записать двумя способами: = x1 +y1 +z1 и = x2 +y2 +z2 , где x1 x2 или y1y2 , или z1z2. Вычитая из первого равенства второе, получим = (x1-x2) + +(y1-y2) +(z1-z2) .
Здесь справа стоит вектор, выражающий диагональ параллелограмма или параллелепипеда, или отрезок на одной из осей Ox, Oy, Oz, который не является нулевым. Противоречие.
Из последнего рассуждения следует, что базисные вектора линейно независимы.
Определение. Коэффициенты линейной комбинации базисных векторов, выражающие вектор на прямой, в плоскости или в пространстве называются, координатами вектора в данном базисе.
Вектор, лежащий на прямой, имеет одну координату x, на плоскости – две координаты x, y; в пространстве – три координаты x, y, z.
