
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
2 Производные и дифференциалы высших порядков
Производная
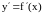 называется еще первой производной
функции
или производной первого порядка, сама
функция
называется производной нулевого порядка.
называется еще первой производной
функции
или производной первого порядка, сама
функция
называется производной нулевого порядка.
Определение.
Производной
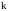 –
го порядка функции называется производная
от её производной (
-1)
порядка при условии, что эти производные
существуют
–
го порядка функции называется производная
от её производной (
-1)
порядка при условии, что эти производные
существуют
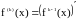 ,
=1,2,3,…
,
=1,2,3,…
функция f при этом называется раз дифференцируемой..
Пример. Дано
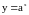 .
.
Первая производная
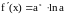 ,
,
вторая производная
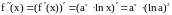 ,
,
третья производная
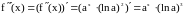 .
.
Следовательно,
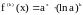 ,
,
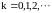 .
.
Эта функция
бесконечно дифференцируема для
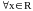 ,
т.е. она имеет производные всех порядков.
Для суммы и произведения
–раз
дифференцируемых функций
и
,
т.е. она имеет производные всех порядков.
Для суммы и произведения
–раз
дифференцируемых функций
и
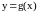 справедливы следующие правила
дифференцирования (
справедливы следующие правила
дифференцирования (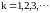 ):
):
1.
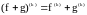 ,
,
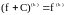 .
.
2. Формула Лейбница:
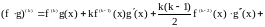
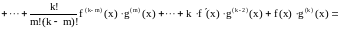
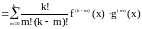 ;
;
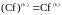 .
.
Без доказательства.
Пример.
Вычислить
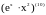 по формуле Лейбница.
по формуле Лейбница.
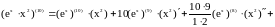
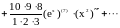 .
.
Заметим, что
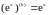 и
и
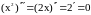 ,
поэтому
,
поэтому
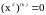 при
при
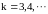 и последующие слагаемые также равны
нулю, следовательно,
и последующие слагаемые также равны
нулю, следовательно,
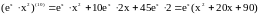 .
.
Пусть функция
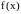
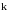 –раз
дифференцируема.
–раз
дифференцируема.
Определение.
Дифференциалом
–го
порядка называется дифференциал от ее
дифференциала
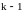 –го порядка
–го порядка
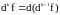 ,
,
вычисленный в
предположении, что
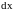 остается постоянной.
остается постоянной.
Получаем формулы для вычисления такого дифференциала:
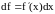 ,
,
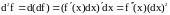 ,
,
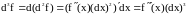 ,
,
… … … … … … … … … … … … … … …
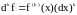 .
.
Из последней формулы имеем еще одно обозначение для производной –го порядка.
Для дифференциалов –го порядка также справедливы следующие правила:
1)
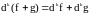 ,
,
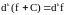 .
.
2)
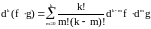 ,
,
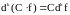 .
.
3. Приложения производной
1. Основные теоремы дифференциального исчисления
Определение.
Точка
называется точкой
минимума (максимума)
функции,
,
если она определена в некоторой
окрестности
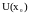 этой точки и для
этой точки и для

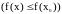 .
.
Значение
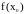 в этом случае называется минимумом
(максимумом)
функции. Точки минимума и максимума
называются экстремальными
точками,
а соответствующие значения
функции–экстремумами.
в этом случае называется минимумом
(максимумом)
функции. Точки минимума и максимума
называются экстремальными
точками,
а соответствующие значения
функции–экстремумами.
Функция, определенная
на отрезке
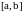 ,
имеет там только одно наибольшее и
наименьшее значения, но может иметь
несколько максимумов и минимумов. При
этом некоторые максимумы могут быть
меньше минимумов (рис.2).
,
имеет там только одно наибольшее и
наименьшее значения, но может иметь
несколько максимумов и минимумов. При
этом некоторые максимумы могут быть
меньше минимумов (рис.2).
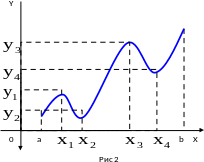
Здесь
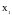 и
и
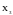 – точки максимумов,
– точки максимумов,
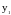 и
и
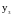 – максимумы;
– максимумы;
 и
и
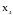 –
точки минимумов;
–
точки минимумов;
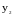 и
и
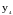 – минимумы;
– минимумы;
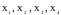 – экстремальные точки,
– экстремальные точки,
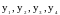 –
экстремумы.
–
экстремумы.
Теорема Ферма.
Пусть
–
точка минимума, т.е.
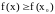 для
для
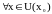 .
.
Тогда для
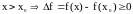 ,
,
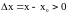 и
и
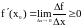 .
.
Для
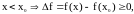
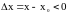 и
и
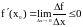 .
.
Следовательно,
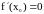 .
.
Заметим, что если
,
то касательная к графику функции
в этой точке параллельна оси
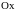 (так
как тангенс угла наклона этой касательной
равен нулю). Поэтому геометрический
смысл теоремы Ферма состоит в том, что
касательная в экстремальной точке
функции (если она существует) параллельна
оси
(рис3).
(так
как тангенс угла наклона этой касательной
равен нулю). Поэтому геометрический
смысл теоремы Ферма состоит в том, что
касательная в экстремальной точке
функции (если она существует) параллельна
оси
(рис3).

и
– точки минимума, в
– касательная параллельна оси
,
в точке
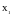 касательной нет.
касательной нет.
Следующие три теоремы выявляют свойства функций, дифференцируемых на отрезке.
Определение.
Функция
называется дифференцируемой на отрезке
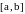 ,
если она непрерывна на этом отрезке и
имеет производную во всех точках
интервала
,
если она непрерывна на этом отрезке и
имеет производную во всех точках
интервала
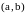 .
.
Для таких функций кроме теорем Больцано–Коши и Вейерштрасса справедливы еще следующие теоремы.
Теорема Ролля.
Пусть
функция
дифференцируема на отрезке
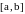 и принимает на его концах равные
значения:
и принимает на его концах равные
значения:
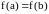 .
Тогда
.
Тогда
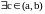 такая, что
такая, что
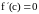 .
.
Геометрический смысл этой теоремы состоит в том, что при выполнении ее условий , в которой касательная к графику функций параллельна оси и хорде, соединяющей концы графика на отрезке (рис.4).

Рис.4
Рис 12
Пример. В
интервале (–1,1) нет точек, в которых
касательная к графику
параллельна оси
.
Здесь нарушается условие теоремы Ролля:
в точке
функция
не дифференцируема, хотя
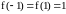 .
.
Теорема Коши.
Пусть функция
и
дифференцируемы на
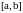 и
и
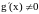 для
для
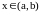 .
Тогда
такая, что
.
Тогда
такая, что
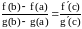 .
.
Следующая теорема является прямым следствием теоремы Коши, однако, в силу ее широкого применения имеет специальное название.
Теорема Лагранжа. Пусть функция дифференцируема на . Тогда в интервале :
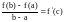 .
.
Заметим, что
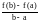
равна тангенсу
угла наклона хорды, соединяющей концы
графика
на
,
а
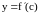 равна тангенсу угла наклона касательной
к графику функции в точке
равна тангенсу угла наклона касательной
к графику функции в точке
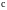 (рис.5).
(рис.5).

Из равенства этих углов получаем геометрический смысл теоремы Лагранжа. При выполнении условий этой теоремы , в которой касательная к графику параллельна хорде, соединяющей концы графика.
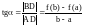 ,
,
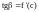 .
.
Следствие
1.
Возьмем
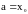 ,
,
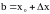 ,
тогда при выполнении условий теоремы
Лагранжа в отрезке
,
тогда при выполнении условий теоремы
Лагранжа в отрезке
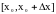 будем иметь
будем иметь
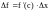 ,
где
,
где
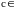
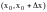 .
.
Это можно записать в виде
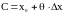 ,
где
,
где
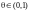 .
.
Тогда приращение функции записывается в виде
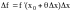
или
в общем виде
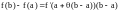 .
.
Следствие
2. Пусть
функция
дифференцируема и
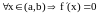 ,
тогда эта функция постоянна в
,
тогда эта функция постоянна в
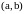 ,
т. е.
,
т. е.
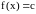 .
.
