§ 2.6. Векторное произведение векторов и его свойства.

Это произведение определено только для пространственных векторов и , и оно обозначается символам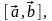и или

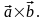
Определение. Векторным произведением векторов и называется вектор 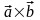, удовлетворяющий трём условиям:

а) Модуль вектора равен произведению модулей векторов и на синус угла между ними:

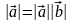sin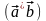

в) перпендикулярен векторам и  т.е. он перпендикулярен плоскости, проходящей через вектора и .

с) Тройка векторов 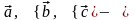правая (см. рис. 2.18).

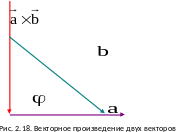
Пример 1. Найдем .

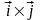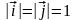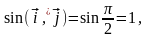Поскольку и то

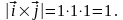
Вектор перпендикулярен векторам 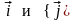, т.е. он направлен вдоль оси 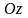и образует правую тройку с векторами . Этим свойством обладает только вектор , т.е.

.

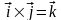Отметим следующие свойства векторного произведения.

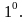В отличие от скалярного произведения векторное произведение

антикоммутативно т.е. для любых векторов и верно:

.

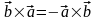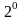. Ненулевые векторы 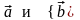коллинеарны только в том случае когда .

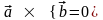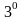. Постоянный множитель можно выносить за знак векторного произведения т.е. для любых векторов и числа верно

:

.

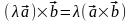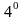. Векторное произведение обладает свойством дистрибутивности т.е. для любых векторов 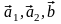верно .

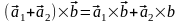Теорема. Пусть в базисе векторы имеют координаты и соответственно.

Тогда в этом базисе

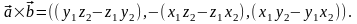
Для запоминания этой формулы используется её запись в виде условного определителя:

,

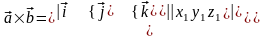который необходимо разложить по первой строке.

Пример2. Из того что 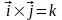следует, что .

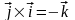Пример3. .

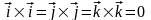Пример4. Пусть 

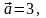
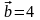
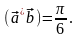
Найдем

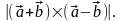
Из-за некоммутативности векторного произведения правила тождественных преобразований для этого произведения не применяются для вычисления модуля вектора используются свойства и определения этого произведения.

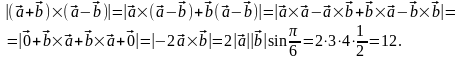
Пример5. Пусть

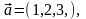
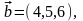
Найдем .

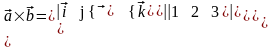
Векторное произведение, в частности, применяется для нахождения координат векторов перпендикулярных двум заданным векторам. В последнем примере вектор 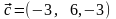перпендикулярен векторам 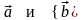и образует с ними правую тройку. Другое приложение векторного произведения связано с задачей нахождения площадей. Заметим что модуль векторного произведения 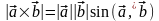равен площади параллелограмма, построенного на векторах . Площадь треугольника образованного этими векторами равна

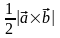
Отсюда получаем следующее.

Следствие 1. Площадь параллелограмма построенного на векторах и , равна:

.

Площадь треугольника, построенного на этих векторах, равна:

.

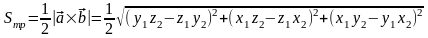Пример6. Найдем площадь треугольника АВС где

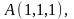
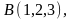
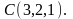
Для её нахождения используем векторы 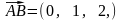и

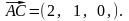
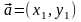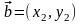Следствие 2. Площадь параллелограмма построенного на векторах и , лежащих в плоскости , равна:

.

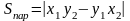Площадь треугольника построенного на векторах, равна:

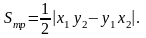
Эти формулы получаются из формул следствия 1 путем подстановки туда

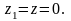
Получим: .

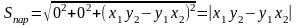Последнюю формулу можно такие записать в виде:

.

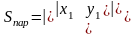Другие приложения векторного произведения будут рассмотрены в 11-м модуле, изучаемом в третьем семестре.