
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
3 Бесконечно малые и бесконечно большие функции.
Определение.
Функция
 называется
бесконечно малой
(б. м.) при
называется
бесконечно малой
(б. м.) при
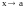 ,
если
,
если
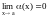
или

Пример.
Функция
 является б.м. при
является б.м. при
 и не является таковой при
и не является таковой при
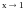 .
.
Теорема 1.
Пусть
 — б.м. при
— б.м. при
 ,
тогда их сумма
,
тогда их сумма

также является
б.м. при
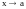 .
.
Теорема 2.
Пусть
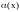 б. м. при
б. м. при
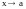 ,
а
,
а
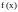 ограничена в некоторой окрестности
точки а,
тогда
ограничена в некоторой окрестности
точки а,
тогда
 является б. м. при
.
является б. м. при
.
Пример.
Вычислим
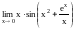 .
.
При
величина х является б. м., а функция
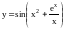 ограничена, так как
ограничена, так как
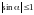 .
.
Следовательно, искомый предел, как предел б. м., равен нулю.
Теорема 3.
Предел
равен числу А
в том и только в том случае, когда
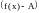 является б. м. при
.
является б. м. при
.
Пример.
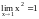 означает, что
означает, что
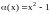 является б. м. при
.
является б. м. при
.
Из этого свойства
следует, что функцию
 ,
имеющую предел А при
,
можно записать в виде
,
имеющую предел А при
,
можно записать в виде
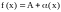 ,
где
,
где
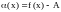 есть б. м. при
.
есть б. м. при
.
Аналогично при
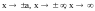 .
.
3.1 Основные
теоремы о пределах. Пусть
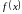 и
и
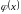 - функции, для которых существуют пределы
при
(или при
- функции, для которых существуют пределы
при
(или при
 ):
):
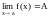 ,
,
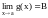 .
Сформулируем основные теоремы о пределах.
.
Сформулируем основные теоремы о пределах.
Функция не может иметь более одного предела.
Предел алгебраической суммы, то тогда
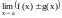 существует и равен
существует и равен
А В.
Если и существуют, то тогда
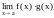 существует и равен
существует и равен
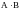 .
.
Если и и
 существуют, то тогда
существуют, то тогда
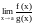 существует и равен
существует и равен
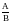 .
.
Первый замечательный предел
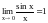 .
.
Доказательство.
Пусть
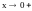 и
и
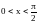 .
Рассмотрим круг единичного радиуса с
центральным углом АОВ=х.
(см. рис.8).
.
Рассмотрим круг единичного радиуса с
центральным углом АОВ=х.
(см. рис.8).
Из рис.34
непосредственно видно:
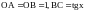 .
.
 сектора
сектора
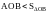
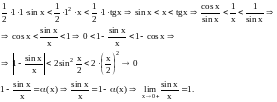
 .
.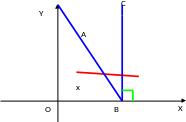
Рис. 8
Так как функция
 чётная, то
чётная, то
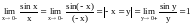 .
.
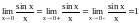 .
.
Пример.
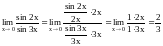 .
.
Второй замечательный предел
 .
.
Здесь е 2,718282… – иррациональное число.
Доказательство. Мы докажем следующее утверждение:
 существует и
2
е
3.
существует и
2
е
3.
Для этого воспользовавшись формулой бинома Ньютона:

 ,
,
где
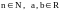 ,
получаем:
,
получаем:
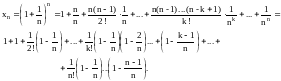
Эта последовательность {хn} обладает двумя свойствами:
а) Она монотонно возрастает, так как в xn+1 на одно слагаемое больше, и каждое слагаемое в xn+1 больше соответствующего слагаемого в {хn}.
б)
 ,
,
т. е. {хn}
ограничена сверху числом 3. Следовательно,
по свойству 4 пределов
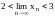
Пример. Вычислим предел
3.2 Бесконечно большие функции и их свойства
Определение. Функция y=F(x) называется бесконечно большой (б.б.) при x a, если
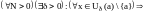
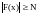 .
.
Это обозначается
символом
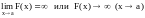 ,
хотя предел этой функций при
не существует.
,
хотя предел этой функций при
не существует.
Пример.
Функция
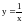 является б.б. функцией при
является б.б. функцией при
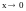 ,
так как
,
так как
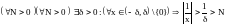 .
.
Очевидно, что любая
б.б. функция не ограничена в окрестности
точки
 .
.
Если
 и в некоторой окрестности точки а
функция
и в некоторой окрестности точки а
функция
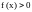 (соответственно
(соответственно
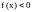 ),
то еще пишут
),
то еще пишут
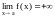 (соответственно
(соответственно
 ).
).
Отметим следующие свойства б.б. функций.
Сумма двух б.б. одного знака при является б.б. при .
Сумма б.б. функции при и ограниченной в окрестности точки а функции является б.б. при .
Пример.
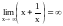 ,так
как х- есть б. б. при
,
а
,так
как х- есть б. б. при
,
а
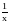 б. м., следовательно, ограниченная функция
при
б. м., следовательно, ограниченная функция
при
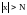 .
.
Если
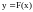 б. б. при
,
а
б. б. при
,
а
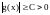 в некоторой окрестности точки
а,
то функция
в некоторой окрестности точки
а,
то функция
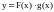 является б. б. при
является б. б. при
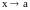 .
В частности, произведение двух б. б. и
произведение б. б. на функцию, имеющую
ненулевой предел, является б. б.
.
В частности, произведение двух б. б. и
произведение б. б. на функцию, имеющую
ненулевой предел, является б. б.
Пример.
 ,
так как х –
б.б. и
,
так как х –
б.б. и
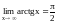 .
.
Если
 б.
б. при
,
то
б.
б. при
,
то
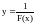 б.м. при
.
б.м. при
.Если
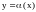 б.м. при
и
б.м. при
и
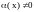 при
при
 то
то
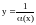 является б.б. при
.
является б.б. при
.
Пример:
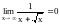 ,
так как
,
так как
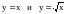 б. б. одного знака при
б. б. одного знака при
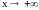 .
.
Сравнение бесконечно малых и бесконечно больших
Определение.
Бесконечно
малая
называется б.м. высшего порядка малости
по сравнению с б.м.
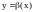 при
в случае, если найдётся б.м.
при
в случае, если найдётся б.м.
 при
такая, что
при
такая, что
 .
Соответствующее обозначение
.
Соответствующее обозначение
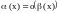 .
.
Пример:
При
 ,
так как
,
так как
 и
и
 есть б.м. при
.
есть б.м. при
.
При
 :
:
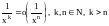
Определение.
Бесконечно
малые
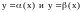 при
называются эквивалентными, если
при
называются эквивалентными, если
 .
Обозначение
.
Обозначение

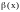 .
Подобное определение даётся и для б.б.
функции.
.
Подобное определение даётся и для б.б.
функции.
Пример.
Б.м.
 эквивалентны при
,
это следует из первого замечательного
предела.
эквивалентны при
,
это следует из первого замечательного
предела.
Это отношение эквивалентности удовлетворяет трём свойствам
;
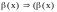
 ;
;Если
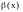 и
и
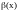
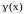 ,
то
,
то
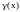 .
.
Теорема.
Из
следует,
что
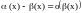 .
.
Теорема.
Пусть
есть б. м. при
 ,
тогда:
,
тогда:
 ;
;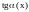
;
;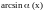
;
;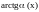
;
;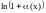
;
;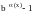
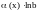 ,
,
 ;
;
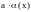 .
.
Эти эквивалентные б.м. позволяют более просто вычислять некоторые пределы с помощью следующей теоремы.
Теорема.
Пусть

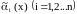 при
,
тогда
при
,
тогда
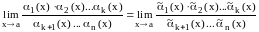 .
.
При этом оба записанных предела существуют одновременно. Если одно из выражений б. б., то другое также является б. б.
Пример.
 ,
,
так как
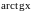
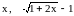
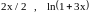
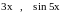
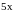 .
.
