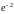- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
Асимптоты графика функции
Определение. Прямая L называется асимптотой для кривой k, если расстояние от точки M на k до L стремится к нулю при удалении M в бесконечность (т.е. при |OM| ) (рис.8).

Асимптоты графика функции y=f(x) (коротко говорят асимптоты функции) делятся на два вида:
вертикальные асимптоты, т.е. прямые, параллельные оси Оy, они имеют уравнения вида х=х0;
наклонные асимптоты, т.е. прямые, не параллельные оси Оy; они имеют уравнения вида y=kx+b.
Ясно, что функция может иметь сколько угодно вертикальных асимптот и не более двух наклонных: правую и левую. Правая асимптота определяется при абсциссе х +, а левая при х –.
Примеры:
Функция y=x2 не имеет асимптот.
Функция y=tgx имеет бесконечное множество вертикальных асимптот вида
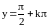 ,
,
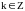 и не имеет наклонных асимптот.
и не имеет наклонных асимптот.Функция y=1/x имеет вертикальную асимптоту x=0, для левой и правой ветвей гиперболы и левую и правую наклонную асимптоту y=0.
Функция y=|x| имеет левую наклонную асимптоту y= –x и правую y=x. Вертикальных асимптот у нее нет.
Теорема (о вертикальной асимптоте). Прямая х=х0 является вертикальной асимптотой функции y=f (x) только в том случае, когда при х х0 – или х х0+ эта функция является бесконечно большой.
Геометрический смысл этой теоремы ясен.
Пример.
Найти вертикальные асимптоты функции
 .
.
Очевидно, что значения х0, определяющие вертикальные асимптоты, лежат среди точек разрыва этой функции. Таких точек две: х1= –1, x2= +1.
 ,
,
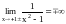 .
.
Поэтому функция имеет две вертикальные асимптоты х= –1, x=+1 (рис. 23).

Теорема (о наклонной асимптоте). Прямая y=kx+b является правой (левой) наклонной асимптотой функции y=f (x) в том и только том случае, когда существуют (конечные) пределы
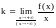 и
и
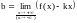 .
(5.3)
.
(5.3)
Пример.
Найти асимптоты гиперболы
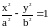 .
.
Эта гипербола
состоит из двух графиков функций
 .
.
Рассмотрим случай положительного корня. Для правой асимптоты
 =
= =
=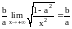
 =
=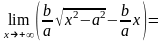
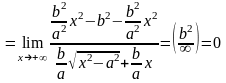 .
.
Следовательно,
правая асимптота имеет вид
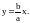

Аналогично
проверьте, что левая асимптота
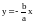
Схема исследования и построения графика функции
Чтобы исследовать функцию y=f (x) и построить ее график, действия рекомендуется проводить в следующем порядке.
Нахождение области определения функции. Исследование на четность, нечетность, периодичность. Нахождение точек пересечения графика с осями координат.
Исследование функции на непрерывность. Вычисление пределов функции при
 ,
стремящемся к границам области
определения и к точкам разрыва.
,
стремящемся к границам области
определения и к точкам разрыва.
Нахождение асимптот функции.
Вычисление f ' (x) и исследование ее знаков. Нахождение интервалов возрастания, убывания и экстремумов.
Вычисление f ''(x) и исследование ее знаков. Нахождение интервалов направления выпуклости и точек перегиба.
Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.
Построение графика функции с учетом ее асимптот и таблицы. При необходимости можно вычислить промежуточные значения функции.
Пример.
Исследовать функцию
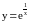 и построить ее график.
и построить ее график.
Функция определена в области D=(-,0) (0, ). С осями координат график не пересекается, так как при х=0 она не определена и f(x)>0 xD. Функция не является четной, нечетной и периодичной.
Функция непрерывна в своей области определения, х0=0 – ее точка разрыва.


Следовательно, прямая х=0 – вертикальная асимптота
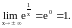
 ,
,
 .
Поэтому прямая y=
=1 является
правой и левой наклонной асимптотой
функции.
.
Поэтому прямая y=
=1 является
правой и левой наклонной асимптотой
функции.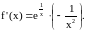 Знаки этой производной следующие
(рис.11).
Знаки этой производной следующие
(рис.11).

Р
Поэтому на промежутках (-,0) и (0,) функция убывает.
Критических точек и экстремумов нет.
 Знаки f
''(x)
(рис.12) В промежутке
Знаки f
''(x)
(рис.12) В промежутке
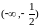 функция выпукла вверх, в промежутках
функция выпукла вверх, в промежутках
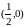 ,
,
 она выпукла вниз. Критическая точка
второго порядка является точкой перегиба
функции.
она выпукла вниз. Критическая точка
второго порядка является точкой перегиба
функции.

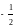 o
o
6.
X |
(-,- |
- |
(- ,0 ) |
0 |
(0, +) |
f '(x) |
|
|
|
не |
|
f ''(x) |
|
0 |
+ |
не |
+ |
f (x) |
|
|
|
не |
|
точка точка перегиба разрыва 2-го рода
Построение графика начинаем с асимптот и критических точек, затем пользуемся таблицей (рис.13).

Рис 13

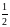 )
)