§ 1.2. Миноры и алгебраические дополнения. Разложение

определителя по элементам строки или столбца

Дальнейшие свойства связаны с понятиями минора и алгебраического дополнения

Определение. Минором элемента называется определитель , составленный из элементов, оставшихся после вычеркивания i-ой стоки и j-го стобца, на пересечении которых находится этот элемент.

Минор элемента определителя n-го порядка имеет порядок (n-1). Будем его обозначать через .

Пример 1. Пусть

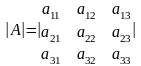
 тогда .

Этот минор получается из A путём вычёркивания второй строки и второго столбца.

Определение. Алгебраическим дополнением элемента называется соответствующий минор, умноженный на т.е

A_ij=(–1)^i+j M_ij,

где i –номер строки и j -столбца, на пересечении которых находится данный элемент.

8⁰. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.

Пример 2.

Пусть , тогда

,

.

Пример 3.

Найдём определитель матрицы , разложив его по элементам первой строки.

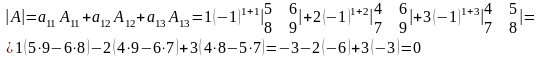
Формально эта теорема и другие свойства определителей применимы пока только для определителей матриц не выше третьего порядка, поскольку другие определители мы не рассматривали. Следующее определение позволит распространить эти свойства на определители любого порядка.

Определение. Определителем матрицы A n-го порядка называется число, вычисленное с помощью последовательного применения теоремы о разложении и других свойств определителей.

Можно проверить, что результат вычислений не зависит от того, в какой последовательности и для каких строк и столбцов применяются вышеуказанные свойства. Определитель с помощью этого определения находится однозначно.

Хотя данное определение и не содержит явной формулы для нахождения определителя, оно позволяет находить его путём сведения к определителям матриц меньшего порядка. Такие определения называют рекуррентными.

Пример 4.

Вычислить определитель: .

Хотя теорему о разложении можно применять к любой строке или столбцу данной матрицы, меньше вычислений получится при разложении по столбцу, содержащему как можно больше нулей.

Поскольку у матрицы нет нулевых элементов, то получим их с помощью свойства 7). Умножим первую строку последовательно на числа (–5), (–3) и (–2) и прибавим её ко 2-ой, 3-ей и 4-ой строкам и получим:

.

Разложим получившийся определитель по первому столбцу и получим:

( вынесем из 1-ой строки (–4), из 2-ой — (–2), из 3-ей — (–1) согласно свойству 4)

(так как определитель содержит два одинаковых столбца).

§ 1.3. Некоторые виды матриц и их определители

Определение. Квадратная матрица, у которой ниже главной диагонали стоят нулевые элементы ( =0 при ij) называется верхнетреугольной. Матрица, у которой выше главной диагонали стоят нулевые элементы ( =0 при ij) называется нижнетреугольной.

Их схематичное строение соответственно имеет вид:

и

Здесь 0 – означает нулевые элементы, а – произвольные элементы.

Верхне и нижнетреугольные матрицы называются треугольными.

Теорема. Определитель квадратной треугольной матрицы равен произведению её элементов, стоящих на главной диагонали, т.е.

.

Например:

Определение. Квадратная матрица, у которой вне главной диагонали стоят нулевые элементы, называется диагональной.

Её схематический вид:

Диагональная матрица является и верхне – и нижнетреугольной, поэтому её определитель также равен произведению элементов, стоящих на главной диагонали.

Диагональная матрица, у которой на главной диагонали стоят только единичные элементы называется единичной матрицей. Она обозначается через:

Определитель единичной матрицы равен 1, т.е. E=1.

Матрица произвольных размеров

где при , называется квазитреугольной (ступенчатой или трапециевидной).