
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
2 Правило Лопиталя
Это правило дает
возможность вычислять пределы
дифференцируемых функций вида
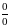 или
или
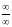 с использованием производных.
с использованием производных.
Теорема. Пусть
и
две б.м. или б.б. при
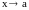 функции, дифференцируемые в
функции, дифференцируемые в
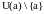 и пусть
и пусть
 и
в
.
Тогда, если существует
и
в
.
Тогда, если существует
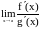 ,
то существует
,
то существует
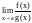 и
они равны:
и
они равны:
=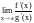 .
.
Аналогичные
утверждения справедливы для
 ,
,
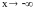 ,
,
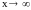 ,
,
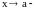 ,
,
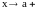 ,
а также для случая, когда
,
а также для случая, когда
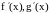 является б.б.
является б.б.
Примеры.
 ;
;Если в результате применения правила Лопиталя получается неопределенность вида
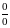 и
,
то это правило можно применить несколько
раз:
и
,
то это правило можно применить несколько
раз:
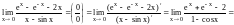
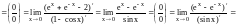
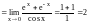 .
.
К пределам других
видов
 также можно применять правило Лопиталя,
предварительно преобразовав выражение
к виду
также можно применять правило Лопиталя,
предварительно преобразовав выражение
к виду
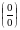 или
или
 .
.
Произведение б.м. на б.б. функцию
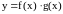 ,
т.е. вида
,
т.е. вида
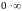 ,
преобразуется к виду
,
преобразуется к виду
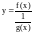 (вида
)
или
(вида
)
или
 (вида
).
(вида
).
Затем применяется правило Лопиталя.
Пример.
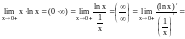
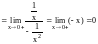 .
.
Разность двух б.б. функций
 вида
вида
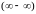 преобразуется, например, к виду
преобразуется, например, к виду
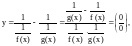
к этому выражению применяется правило Лопиталя.
Пример.
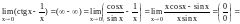
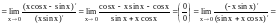
 =
=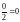 .
.
3. Функция
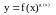 типа
типа
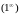 или
или
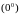 записывается в виде
записывается в виде
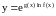 ,
,
затем вычисляется
 типа
типа
 .
.
Если
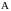 – число, то
– число, то
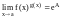 .
.
Если
=
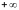 ,
то
,
то
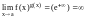 .
.
Если
 ,
то
,
то
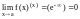 .
.
Пример. Вычислим
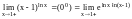 ,
для этого вычислим предел:
,
для этого вычислим предел:

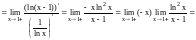
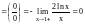 ,
,
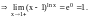
Контрольные вопросы:
1.Сформулируйте определения производной и дифференциала высших порядков.
2. Инвариантность формы первого дифференциала
3. Формула приближенного вычисления значения функции
4. Правило нахождение производных высшего порядка. Примеры
5. Теоремы Ролля, и ее геометрический смысл
6. Теорема Лагранжа и ее геометрический смысл
Литература:
Основная [2] Глава 4 § 4.1-4.8 стр. 151-178, [19] 3.3-3.6 стр. 191-209, [18] §10.1-10.4 стр. 265-273
[20] §10.1-10.4 стр. 184-192
Тема 9 Исследование поведения функции и их графиков.
Определение.
Функция
называется строго
возрастающей (убывающей) в
интервале (a,b),если
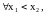
 выполняется
выполняется
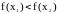 (или
(или
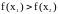 )
(сравните с
понятием монотонного возрастания и
убывания).
)
(сравните с
понятием монотонного возрастания и
убывания).
Следующая теорема позволяет найти интервалы возрастания и убывания функций с помощью ее производной.
Теорема. Пусть y=f(x) дифференцируема в (a,b):
Если f(x) монотонно возрастает в (a,b) , то
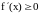 ,
,
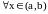 .
.
2. Если , , то f(x) монотонно возрастает в (a,b).
Аналогичная теорема имеет место и для убывающих функций. Итак, в интервалах возрастания или убывания функции знак производной не меняется.
Пример. Найти интервалы возрастания и убывания функции
y = x3 – 3x2 + 1.
Для этого определим интервалы знакопостоянства ее производной
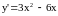 .
.
Этот квадратный
трехчлен имеет корни x1=0,
x2=2,
поэтому при
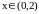
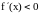 и в этом промежутке функция y
= x3
– 3x2
+ 1 строго убывает.
и в этом промежутке функция y
= x3
– 3x2
+ 1 строго убывает.
При
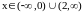 ,
f'(x)>0
и в этих промежутках функция строго
возрастает. Так как f(0)=1
и f(+2)=
3, то эскиз графика функции имеет вид
(рис.1).
,
f'(x)>0
и в этих промежутках функция строго
возрастает. Так как f(0)=1
и f(+2)=
3, то эскиз графика функции имеет вид
(рис.1).
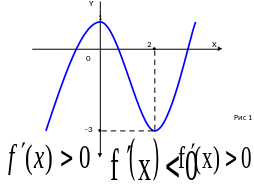
Вспомните теперь определение экстремальных точек функции.
Определение. Точка x0 , в которой f(x0) непрерывна, а производная функции y=f(x) равна нулю или не существует, называется критической точкой этой функции.
Теорема (необходимое условие экстремума). Пусть x0 – экстремальная точка функции y=f(x), тогда x0 – критическая точка этой функции.
Пример . Функция y = x3 имеет критическую точку x0=0, так как это единственное решение уравнения f '(x)=3x2=0.
Однако экстремальных точек у этой функции нет, y=x3 строго возрастает на всей числовой оси.
Теорема (достаточное условие экстремума). Пусть функция y=f(x) непрерывна в окрестности U(x0) критической точки x0 и дифференцируема в U(x0) кроме быть может самой точке x0. Тогда
1) если в U(x0) f ' (x)>0 при х<x0 и f '(x)<0 при x>x0 , то x0 точка максимума;
2) если в U(x0) f ' (x)<0 при х<x0 и f '(x)>0 при x>x0 , то x0 точка минимума;
3) если в U(x0) f ' (x)>0 или f '(x)<0 при x x0 , то в x0 экстремума нет.
Итак, чтобы определить экстремальные точки функции необходимо найти все ее критические точки и установить знаки производной в интервалах между ними. Затем согласно достаточному условию экстремума исследуются найденные критические точки. Точки непрерывности функции, где производная меняет свой знак с "плюса" на "минус", являются точками максимума; точки, где производная меняет свой знак с "минуса" на "плюс", являются точками минимума; точки, где производная свой знак не меняет, экстремальными не являются.
Пример.
Исследовать функцию
 на возрастание, убывание и экстремумы.
на возрастание, убывание и экстремумы.
Производная функции
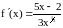
не существует при x1=0.
Из уравнения
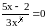 получаем вторую критическую точку
получаем вторую критическую точку
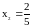 .
Методом интервалов определяем знаки
f
'(x)
(рис.2).
.
Методом интервалов определяем знаки
f
'(x)
(рис.2).

Функция
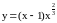 всюду непрерывна; согласно достаточному
условию экстремума x1=0
есть точка максимума, а
всюду непрерывна; согласно достаточному
условию экстремума x1=0
есть точка максимума, а
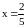 точка минимума. В интервалах (–,
0) и
точка минимума. В интервалах (–,
0) и
 эта функция возрастает, а в интервале
эта функция возрастает, а в интервале
 она убывает. Результаты исследования
занесем в таблицу
она убывает. Результаты исследования
занесем в таблицу
x |
(–,0) |
0 |
(0, |
|
( , +) |
f '(x) |
+ |
не |
– |
0 |
+ |
f |
|
0 max |
|
min |
|
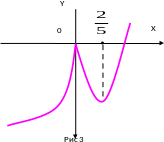
Построим теперь эскиз графика функции, учитывая, что при х0 f '(x) является бесконечно большой (рис.3).
Приведем еще один достаточный признак экстремума, использующий вторую производную функции.
Теорема. Пусть функция y=f(x) дифференцируема в некоторой окрестности критической точки х0 и f ''(x0) существует. Тогда, если f ''(x0)>0, то x0 - точка минимума, а если f ''(x0)<0, то x0 - точка максимума.
Пример . Найти экстремальные точки функции y=2sinx+cos2x.
В
силу ее периодичности достаточно
рассмотреть отрезок [0,2 ].
Найдем критические точки из уравнения
].
Найдем критические точки из уравнения
f ' (x)=2cosx–2sin2x=0 cosx– 2sinxcosx = 0 cosx(1 – 2sinx)=0.
Из
уравнения cosx=0
получаем
 ,
,
 ,
а из уравнения
1 – 2sinx=0
,
а из уравнения
1 – 2sinx=0
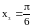 ,
,
 .
.
Вычислим f '' (x)=–2sinx–4cos2x.
 ,
,
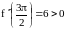 ,
,
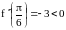 ,
,
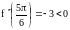 .
.
Итак,
точки
 ,
,
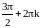 являются точками минимума, а
являются точками минимума, а
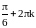 ,
,
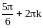 точками максимума (kZ).
График этой функции имеет вид (рис.4).
точками максимума (kZ).
График этой функции имеет вид (рис.4).

С
помощью исследования экстремумов можно
находить наибольшее и наименьшее
значение функции на отрезке. Поскольку
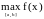 может достигаться или на концах отрезка
[a,b]
или в одной из точек максимума, то для
его нахождения необходимо найти все
максимумы функции в [a,b],
f(a),
f(b)
и затем из этих чисел выбрать наибольшее:
может достигаться или на концах отрезка
[a,b]
или в одной из точек максимума, то для
его нахождения необходимо найти все
максимумы функции в [a,b],
f(a),
f(b)
и затем из этих чисел выбрать наибольшее:
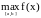 =
max{f(a),
f(b),
f(xi):
xi(a,b)
точки максимумa}.
=
max{f(a),
f(b),
f(xi):
xi(a,b)
точки максимумa}.
Аналогично
 =
min{f(a), f(b), f(xi):
xi(a,b)
точки
минимумa}.
=
min{f(a), f(b), f(xi):
xi(a,b)
точки
минимумa}.
Пример
Найти
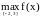 и
и
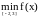 для f(x)=x3–3x+3.
для f(x)=x3–3x+3.
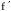 (x)=3x2
–
3 существует для всех х. Из уравнения
3х2
–
3=0 получаем критические точки х1,2=1,
х1,2[–2,3],
f
''(x)=6x,
(x)=3x2
–
3 существует для всех х. Из уравнения
3х2
–
3=0 получаем критические точки х1,2=1,
х1,2[–2,3],
f
''(x)=6x,
 , х1=1
– точка минимума.
, х1=1
– точка минимума.
f '' (–1)= –6<0 x2= –1 точка максимума. Поэтому
f(-2)=1, f(3)=27-9+3=21, f(-1)=-1+3+3=5, f(1)=1-3+3=1
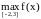 =
max{f
(-2), f
(3), f
(-1)} = max{1,21,5}
= 21.
=
max{f
(-2), f
(3), f
(-1)} = max{1,21,5}
= 21.
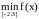 =
min{f
(-2), f
(3), f
(1)} = min{1,21,1}
= 1.
=
min{f
(-2), f
(3), f
(1)} = min{1,21,1}
= 1.

 )
)
 (x)
(x)