
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
4.2 Свойства функций, непрерывных на отрезке
Определение.
Функция
называется непрерывной на отрезке
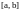 ,
если она непрерывна во всех точках
интервала (а,
),
непрерывна в точке а
справа и в точке
слева.
,
если она непрерывна во всех точках
интервала (а,
),
непрерывна в точке а
справа и в точке
слева.
Обозначение
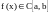 .
.
Первая теорема
Больцано-Коши. Пусть
и принимает на его концах значения
разных знаков (т. е.
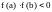
 ),
тогда найдется по крайней мере одна
точка с
в интервале (а,
),
тогда найдется по крайней мере одна
точка с
в интервале (а,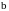 )
такая, что
)
такая, что

Рис. 14
Пример.
Рассмотрим функцию
 на отрезке
на отрезке
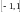 ,
для неё
,
для неё
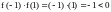 .
Однако это функция нигде не обращается
в нуль. Теорема здесь не применяется,
потому что эта функция имеет разрыв в
точке
.
Однако это функция нигде не обращается
в нуль. Теорема здесь не применяется,
потому что эта функция имеет разрыв в
точке
 ,
и
,
и
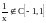 .
(рис.14).
.
(рис.14).
Это даёт алгоритм
приближенного решения уравнения
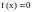 ,
который называется методом
половинного деления.
,
который называется методом
половинного деления.
Пример.
Уравнение
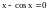 имеет корень на интервале
имеет корень на интервале
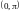 .
В самом деле,
.
В самом деле,
 непрерывна на
непрерывна на
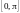 и
и
 ,
,
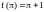 ,
т. е.
,
т. е.
 .
.

Рис.15
Вторая теорема Больцано-Коши. Пусть
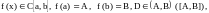
тогда
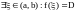 .
.

Рис. 16
Эту теорему можно
сформулировать и так: непрерывная
на отрезке а,
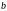
функция
принимает
все
промежуточные значения между
функция
принимает
все
промежуточные значения между
 и f(
).
и f(
).
Первая теорема
Вейерштрасса. Если
.,
то она ограничена на этом отрезке, т. е.
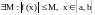 .
.
Пример.
Функция
 непрерывна в интервале (0,1), но не
ограничена на нём, так как
непрерывна в интервале (0,1), но не
ограничена на нём, так как
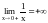 .
.
Поэтому слово “отрезок” в этой теореме существенно.
Определение.
Наибольшим
значением
функции
в промежутке
называется такое значение
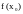 ,
,
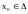 ,
при котором
,
при котором
 для всех
для всех
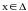 (обозначение
(обозначение
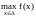 ).
).
Аналогично вводится
понятие наименьшего значения функции
в
(обозначение
 ).
).
Пример.
Функции
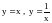 в интервале (-1,1) не принимают ни
наибольшего, ни наименьшего значений.
в интервале (-1,1) не принимают ни
наибольшего, ни наименьшего значений.
Вторая теорема
Вейерштрасса. Функция
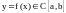 достигает в нём своих наибольшего и
наименьшего значений.
достигает в нём своих наибольшего и
наименьшего значений.
Без доказательства (рис.17).
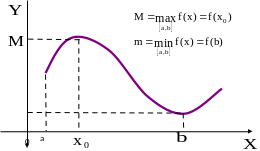
Рис. 17
Контрольные вопросы:
1. Сформулируйте определения предела последовательности, предела функции при стремлении аргумента к некоторому конечному пределу и предела функции при стремлении аргумента к бесконечности.
2.Какая функция называется бесконечно малой и каковы ее основные свойства?
3.Основные теоремы о пределах функций.
4.Первый замечательный предел. Сформулируйте определение числа е (второй замечательный предел).
5.Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции.
6.Сформулируйте основные свойства функций, непрерывных на отрезке и дайте геометрическое истолкование этим свойствам.
Литературы:
Основная [2] глава 3 § 3.3-3.10 стр. 86-126
[19] 2.5-2.7 стр. 162-180
[18] § 5.5-5.10 стр. 146-189
Тема 7. Дифференциальное исчисление. Производная
Задачи, приводящие к понятию производной
Пусть в некоторой
окрестности точки
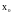 и в самой точке
определена функция
и в самой точке
определена функция
 .
.
Определение:
Приращением
аргумента
х в точке
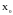 называется разность
называется разность
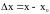 .
.
Определение. Приращением функции в точке называется разность
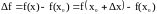 .
.
Это приращение
зависит от двух аргументов
 и x.
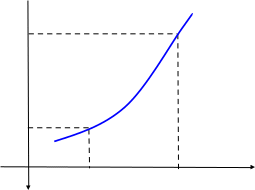
Геометрически x
и f
означают изменения абсциссы и ординаты
точки на графике
при перемещении из точки
и x.
Геометрически x
и f
означают изменения абсциссы и ординаты
точки на графике
при перемещении из точки
 в точку
в точку
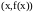 (рис.1).
(рис.1).
 Y
Y
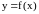
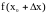 B
B
 A
A
0 X
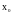

Рис.1
Пример.
Если
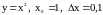 ,
то
,
то
 ,
,
т. е. при увеличении стороны квадрата, равной 1 на 0,1, его площадь возрастает на 0,21.
Используя понятия
x,
y,
можно дать ещё одно определение
непрерывности функции в точке
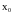 ,
эквивалентное предыдущему.
,
эквивалентное предыдущему.
Определение.
Если функция
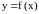 определена в некоторой окрестности
точки
и
определена в некоторой окрестности
точки
и
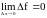 ,
то она называется непрерывной
в точке
.
,
то она называется непрерывной
в точке
.
В самом деле, этот предел означает, что
 ,
т. е.
,
т. е.
 .
.
Определение. Если существует предел

то это число называется производной функции в точке .
Эта производная обозначается также одним из следующих символов:
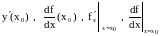 .
.
Этот предел можно записывать также в виде
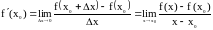
Определение.
Функция
называется дифференцируемой
в точке
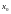 ,
если она имеет конечную производную в
этой точке.
,
если она имеет конечную производную в
этой точке.
Выясним теперь связь между дифференцируемостью и непрерывностью функции, для этого из определения выразим f.
 ,
,
(где
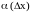 -
б.м. при
-
б.м. при
 (свойство 30
б.м.
, модуль 3)).
(свойство 30
б.м.
, модуль 3)).
Следовательно,
 .
.
Теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Пример.
Функция
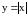 всюду непрерывна, однако она не
дифференцируема при
всюду непрерывна, однако она не
дифференцируема при
 ,
так как
,
так как
 .
.
 , а этот предел,
как мы выше проверяли, не существует.
, а этот предел,
как мы выше проверяли, не существует.
