4.Непрерывность функции
Определение.
Функция
называется непрерывной
в точке
,
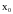если выполняются три условия:
существует
;существует
;
.
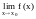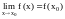В символической форме это определение записывается так:
.
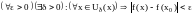Функция
называется непрерывной в точке
слева
(справа), если выполняются три условия:
1)
;
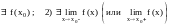2)
.
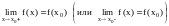Очевидно, что функция является непрерывной в точке в том и только в том случае, когда она непрерывна в этой точке слева и справа.
График непрерывной функции представляет из себя непрерывную линию.
Теорема (о
непрерывности монотонной функции).
Пусть функция
монотонна (монотонно возрастает или
монотонно убывает) на отрезке а,
и принимает все значения из отрезка
,
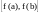тогда она непрерывна в каждой точке
интервала (а,
),
непрерывна
в точке а
справа и в точке
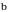слева. (рис.9)
Рис. 9
Из этой теоремы
следует, что все основные элементарные
функции непрерывны во всех внутренних
точках своей области определения, а во
всех граничных точках области определения,
принадлежащих ей, они непрерывны справа
и слева. Это следует из того, что любую
точку из области определения основной
элементарной функции можно включить в
отрезок, где эта функция монотонна и
принимает все значения из отрезка
.
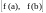Например, функция
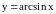непрерывна во всех точках интервала
(–1,1), непрерывна
в точке
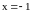справа и в точке
слева, так как оно монотонно возрастает
в
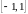и для
.
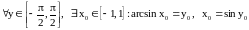Теорема
Пусть функции
и
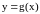непрерывны
в точке
.
Тогда функции
1)
,
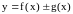2)
,
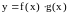3) при
.
также непрерывны в точке .
Теорема
(непрерывность
сложной функции).
Пусть функция
непрерывна в точке
и
,
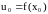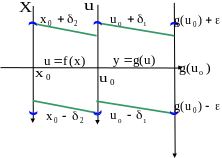а функция
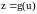непрерывна в точке
.
Тогда сложная функция
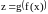непрерывна
в точке
.
Рис. 10
Следствие 1.
Если
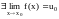и функция
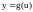непрерывна в точке
,
то
.
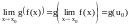Пример.
.
Следствие 2. Любая элементарная функция непрерывна во всех внутренних точках своей области определения, а в граничных точках отрезков области определения непрерывна справа или слева.
Это следует из теорем 1, 2, 3.
4.1 Классификация точек разрыва
Определение. Точка , в которой нарушается хотя бы одно условие непрерывности функции , называется точкой разрыва этой функции.
Рассмотрим точку разрыва функции , в некоторой окрестности которой (кроме быть может ) эта функция определена. Возможны три случая:
1. Если
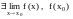не
определена или
,
то
называется точкой устранимого
разрыва.
Если эту функцию изменить в точке , т. е. положить
то функция
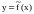будет непрерывной в точке
,
т. е. этот разрыв устраняется.
Пример.
Функция
имеет устранимый разрыв в точке
.
Если положить
то функция
буде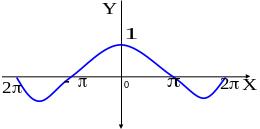
т
всюду непрерывна (рис.11).
Рис.11
График функции
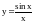
2.
Если
,
то точка
называется точкой
разрыва
первого рода функции
.
Пример. Для функции
точка является разрывом первого рода (рис.12)
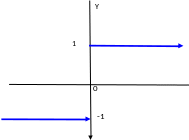
Рис.12
3.
Если хотя бы один из пределов
не существует или равен бесконечности,
то точка
называется точкой
разрыва
второго рода
функции
.
Пример.
Для функции
,
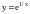точка
является разрывом второго рода, так как
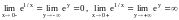(не
существует) (рис.13).
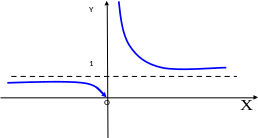
Рис.13