
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
1.3.Элементы поведения функции
Ограниченные
величины и функции. Переменная
величина
называется
ограниченной,
если существует такое число
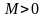 ,
что все значения
попадают
в интервал
,
что все значения
попадают
в интервал
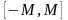 .
Иными словами, для всех значений
выполняется
неравенство
.
Иными словами, для всех значений
выполняется
неравенство
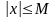
Для функции ограниченность означает выполнение неравенства
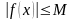 (*)
(*)
при всех
из
области определения. Геометрически это
условие означает, что все точки графика
функции лежат в горизонтальной полосе
между прямыми
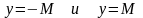 (рис. 7)
(рис. 7)
Так, например,
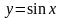 ограниченная
функция, так как
ограниченная
функция, так как
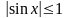 при
всех
.
при
всех
.
Иногда говорят об ограниченности функции лишь на некотором интервале, являющемся частью области определения; это значит, что условие (*) выполняется для рассматриваемого интервала; число может зависеть от взятого интервала.
y M
x

0
-M
Рис. 7
Пример.
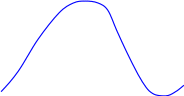
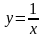 -
функция, не являющаяся ограниченной. В
самом деле, какое бы
мы
не взяли, для тех
,
для которых
-
функция, не являющаяся ограниченной. В
самом деле, какое бы
мы
не взяли, для тех
,
для которых
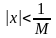 будет выполняться неравенство
будет выполняться неравенство
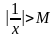 (рис.8).
(рис.8).
 y
y
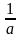
x
0 x
Рис. 8
В то же время на любом интервале
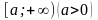 эта функция ограничена:
эта функция ограничена:
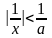 (рис.9). Число
(рис.9). Число
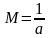 зависит от этого интервала.
зависит от этого интервала.
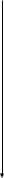 y
y

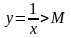
M
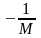 -x 0
-x 0

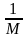 x
x
-M
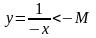
Рис. 9
Возрастание и убывание функций на интервале. Функция называется возрастающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует большее значение функции (рис.10).
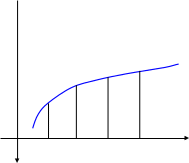
y
0
x1 x2 x
Рис.10
Функция называется убывающей на некотором интервале, если для любых двух значений аргумента, взятых на этом интервале, большему значению аргумента соответствует меньшее значение функции (рис.11).
Запишем эти определения с помощью логических символов - кванторов: для интервала
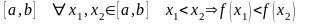 -
условие возрастания;
-
условие возрастания;
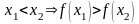 - условие убывания.
- условие убывания.Интервал, на котором функция возрастает или убывает, называется интервалом монотонности этой функции, а про функцию говорят, что она монотонна на этом интервале.
 y
y
0 x1 x2 x
Рис. 11
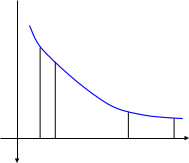
Пример 10.
 (рис.12).
Интервалы монотонности: на
(рис.12).
Интервалы монотонности: на
 функция
убывает; на
функция
убывает; на
 функция возрастает.
функция возрастает.
 y
y

 x
x
0
Рис.12
Четные и нечетные
функции. Пусть
задана функция
![]() с
областью определения
с
областью определения
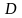 .
Функция
называется четной,
если выполняется условие
.
Функция
называется четной,
если выполняется условие
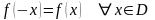
функция называется нечетной, если
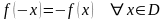
Примеры:
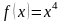 .
Область определения
.
Область определения
 симметрична относительно начала
координат
симметрична относительно начала
координат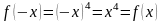 .
Функция четная.
.
Функция четная.
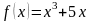 .
Область определения
.
Функция нечетная.
.
Область определения
.
Функция нечетная.
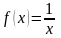 .
Область определения
.
Область определения
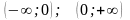 (два интервала) симметрична относительно
начала координат (множество всех
действительных чисел с выброшенным
нулем).
(два интервала) симметрична относительно
начала координат (множество всех
действительных чисел с выброшенным
нулем).
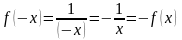 .
Функция нечетная.
.
Функция нечетная.
Из тригонометрии известно, что
 -
нечетные функции;
-
нечетные функции;
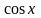 - четная функция.
- четная функция.Геометрически четность функции означает, что ее график симметричен относительно оси ординат. Действительно, наряду с точкой график содержит точку
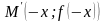 ,
так как
,
так как
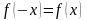 ,
точка
,
точка
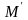 имеет координаты
имеет координаты
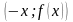 .
Точки
и
оказались
симметричными относительно оси ординат
(рис. 13).
.
Точки
и
оказались
симметричными относительно оси ординат
(рис. 13).
y
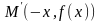



x

-x o x
Рис. 13
Таким образом,
наряду с произвольной точкой
график четной функции содержит и точку,
симметричную ей относительно оси
ординат, а значит, и весь график четной
функции симметричен относительно оси
 (рис.14).
(рис.14).
 y
y
Четная функция


0 x
Рис. 14
Рассуждая аналогичным образом, можно установить, что график нечетной функции симметричен относительно начала координат (рис.15).
y
0 x

Рис. 15
Примеры:
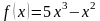 ;
Пусть
;
Пусть
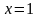 и
и
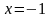 ,
тогда,
,
тогда,
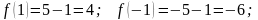 т.е.
т.е.
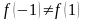 и
и
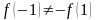 .
Значит, рассматриваемая функция не
является ни четной, ни нечетной.
.
Значит, рассматриваемая функция не
является ни четной, ни нечетной.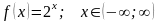 Пусть
и
,
тогда
Пусть
и
,
тогда
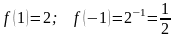 ,
т.е.
и
.
Таким образом, эта функция является
функцией общего вида.
,
т.е.
и
.
Таким образом, эта функция является
функцией общего вида.
Период. Периодические
функции. Число
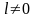 называется
периодом функции
с областью определения
,
если
называется
периодом функции
с областью определения
,
если
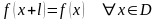
Функция
,
обладающая периодом, называется
периодической.
Условие предполагает, конечно, что
наряду с любым
и
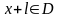
Если число
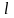 - период функции
,
то и любое целое, кратное
- период функции
,
то и любое целое, кратное
![]() ,
т.е. число
,
т.е. число
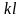 где
где
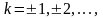 будет
периодом
.
Например,
будет
периодом
.
Например,
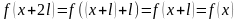 ,
т.е.
,
т.е.
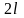 - период;
- период;
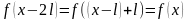 ,
т.е.
,
т.е.
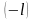 тоже период . В дальнейшем название
периода функции будем применять к
наименьшему положительному периоду.
тоже период . В дальнейшем название
периода функции будем применять к
наименьшему положительному периоду.
Пример.
Из тригонометрии известно, что периоды
функций
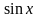 и
равны
и
равны
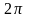 ,
а периоды
,
а периоды
 равны
.
равны
.
График периодической
функции с периодом
достаточно построить на
каком-либо
интервале с длиной, равной периоду, а
затем построенную часть графика сдвигать
вдоль оси
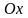 на
на
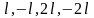 и т. д. (рис. 16).
и т. д. (рис. 16).
Пример. Периодична
ли функция
![]() (показательная)?
Допустим, что периодична. Тогда
(показательная)?
Допустим, что периодична. Тогда
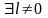 ,
при этом для любого
,
при этом для любого
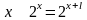 ;
отсюда
;
отсюда
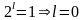 .
.
Это противоречит нашему предположению о существовании периода, значит, предположение неверно. Функция не является периодической.




 y
y


0 l x
Рис.16
Сложная функция (функция от функции). Пусть дана функция от аргумента , причем аргумент
 ,
в свою очередь, является функцией от
независимой переменной
,
в свою очередь, является функцией от
независимой переменной
 :
:
Возьмем
какое-либо значение
.
В силу функциональной зависимости
от
этому значению
отвечает определенное значение
:
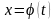 .
Полученному значению
,
в свою очередь, отвечает определенное
значение
.
Полученному значению
,
в свою очередь, отвечает определенное
значение
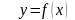 (рис.17)
(рис.17)
y


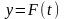
x

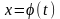

t t
Рис.17
На рис. 17 переменные
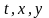 откладываются
на трех осях, изображенных параллельно.
В конечном итоге взятому значению
соответствует определенное значение
откладываются
на трех осях, изображенных параллельно.
В конечном итоге взятому значению
соответствует определенное значение
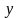 ,
т.е. переменная
оказалась функцией независимой
переменной
.
,
т.е. переменная
оказалась функцией независимой
переменной
.
Получаем
![]() .
Функция
.
Функция
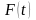 называется сложной
функцией от
независимой переменной
или функцией от функции (функция
от
функции
). При этом функция
называется заданной
или внешней
функцией, а
называется сложной
функцией от
независимой переменной
или функцией от функции (функция
от
функции
). При этом функция
называется заданной
или внешней
функцией, а
![]() -
промежуточным
аргументом.
Функции
и
называют еще составляющими
для сложной функции
; говорят также, что
является суперпозицией
функций
и
.
Чтобы образовать функцию от функции,
нужно, чтобы область значений промежуточной
переменной
"укладывалась" в область определения
заданной функции
(рис.18). В противном случае среди значений
функции
будут и такие, от которых значение
функции
образовать
нельзя (рис. 19). В таких случаях сложную
функцию (или функцию от функции) можно
задать только для тех значений независимой
переменной
,
для которых значения промежуточной
переменной
попадают в область определения внешней
функции
.
-
промежуточным
аргументом.
Функции
и
называют еще составляющими
для сложной функции
; говорят также, что
является суперпозицией
функций
и
.
Чтобы образовать функцию от функции,
нужно, чтобы область значений промежуточной
переменной
"укладывалась" в область определения
заданной функции
(рис.18). В противном случае среди значений
функции
будут и такие, от которых значение
функции
образовать
нельзя (рис. 19). В таких случаях сложную
функцию (или функцию от функции) можно
задать только для тех значений независимой
переменной
,
для которых значения промежуточной
переменной
попадают в область определения внешней
функции
.

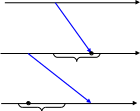
 y
y
Область определения функции
x
Область значений функции
t
Область определения функции
Рис.18
y
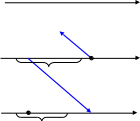
? Область значений функции
x
Область определения функции
t
Область определения функции
Рис.19
Примеры:
1.
![]() .
Область
значений промежуточной переменной
.
Область
значений промежуточной переменной
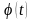 -
отрезок [-1;1]; он не укладывается в область
определения внешней функции
-
отрезок [-1;1]; он не укладывается в область
определения внешней функции
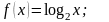 [ее область определения
[ее область определения![]() ].
Поэтому сложную функцию
].
Поэтому сложную функцию
 можно
образовать только для тех значений
аргумента
можно
образовать только для тех значений
аргумента
 ,
для которых
,
для которых
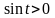 .
.
2.
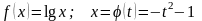 .
Здесь область
значений промежуточного переменного
.
Здесь область
значений промежуточного переменного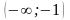 ,
а область определения внешней функции
,
а область определения внешней функции
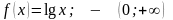 .
Значит, в
этом случае образовать сложную функцию
[т.е. суперпозицию функций
и
]
нельзя.
.
Значит, в
этом случае образовать сложную функцию
[т.е. суперпозицию функций
и
]
нельзя.
Сложные функции могут быть образованы и из большего числа составляющих.
Примеры:
1. у = x3; x = sint, t = 3w + l ; у = F(w) = (sin(3w + l))3 - Здесь два промежуточных аргумента х и t, независимая переменная w.
2.
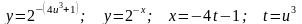 .
.
1.3.2.
Обратная функция. Пусть
на некотором интервале X
задана
функция
,
область
значений
которой обозначим Y
. Согласно
определению функции каждому значению
![]() соответствует
определенное значение
соответствует
определенное значение
![]() .Если
же
интервал X
является
интервалом монотонности для f(x),
то
и каждому
значению
.Если
же
интервал X
является
интервалом монотонности для f(x),
то
и каждому
значению
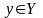 отвечает
одно вполне определенное значение
,
для
которого
у
= f(x)
(рис.20).
Таким образом, в этом случае функциональная
зависимость
между
отвечает
одно вполне определенное значение
,
для
которого
у
= f(x)
(рис.20).
Таким образом, в этом случае функциональная
зависимость
между
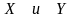 может рассматриваться и как функция
может рассматриваться и как функция
![]() ,
т.е.
можно
рассматривать как аргумент, а
- как функцию. У функции
областью
определения является Y
, а
областью значений - X
. Функции
и
называются
взаимно
обратными
обратная
функция
к функции
;
-
обратная
функция
к функции
.
Уравнение
получается
в результате разрешения, если это
возможно,
уравнения
относительно
переменной
.
,
т.е.
можно
рассматривать как аргумент, а
- как функцию. У функции
областью
определения является Y
, а
областью значений - X
. Функции
и
называются
взаимно
обратными
обратная
функция
к функции
;
-
обратная
функция
к функции
.
Уравнение
получается
в результате разрешения, если это
возможно,
уравнения
относительно
переменной
.
Если f и - взаимно обратные функции, то имеют место тождества (рис.21)
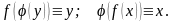
Графиком функции является та же линия, которая изображала функцию y = f(x): ведь уравнение - просто иначе переписанное уравнение у = f(x) .

Рис. 20 Рис. 21
Примеры:
1.
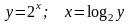 -
обратная
к ней функция. Областью определения
функции
у
=
2х
является
-
обратная
к ней функция. Областью определения
функции
у
=
2х
является
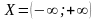 ,
этот же интервал является областью
значений
обратной функции
,
этот же интервал является областью
значений
обратной функции
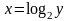 .
Областью значений функции
.
Областью значений функции
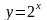 служит
интервал
,
он же является областью определения
для
(рис.22).
Обратная функция в этом примере существует
потому, что
-
возрастающая
функция на всей числовой оси.
служит
интервал
,
он же является областью определения
для
(рис.22).
Обратная функция в этом примере существует
потому, что
-
возрастающая
функция на всей числовой оси.
2. 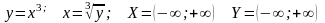 (рис.17).
(рис.17).

Рис.22 Рис.23
Функция
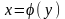 несколько неудобна тем, что, вопреки
привычному, ее аргументом является
,
а не
и значением функции служит
,
а не
.
Неудобство это скорее психологического
характера, однако, чтобы его избежать,
наряду с функцией
рассматривают функцию
несколько неудобна тем, что, вопреки
привычному, ее аргументом является
,
а не
и значением функции служит
,
а не
.
Неудобство это скорее психологического
характера, однако, чтобы его избежать,
наряду с функцией
рассматривают функцию
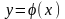 ,
которую также называют обратной функцией
к функции
.
Функция
получается из
переменой ролей
и
:
,
которую также называют обратной функцией
к функции
.
Функция
получается из
переменой ролей
и
:
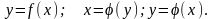

обратные функции к
Примеры:
1.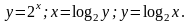

обратные функции к
2.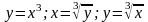
обратные функции к
График обратной функции симметричен графику функции относительно биссектрисы первого и третьего координатных углов.
При таком перегибании
плоскости график нашей функции отобразится
симметрично относительно биссектрисы
первого и третьего координатных углов
(рис.24). На рис.25 показаны графики взаимно
обратных функций
и
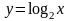 .
.

Рис.24 Рис.25
1.3.3.Неявные
функции. Иногда
функциональная зависимость величин у
и
х
задается
некоторым уравнением,
связывающим х
и
у,
но
нерешенным ни относительно у,
ни
относительно
х.
Например,
уравнение прямой
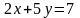 Правда, его очень просто
решить относительно у:
Правда, его очень просто
решить относительно у:
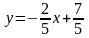 ,
и мы получаем обычное задание функции.
Однако уравнение, связывающее х
и
у
, не
всегда удается разрешить относительно
у
или
х.
Таково,
например, уравнение
,
и мы получаем обычное задание функции.
Однако уравнение, связывающее х
и
у
, не
всегда удается разрешить относительно
у
или
х.
Таково,
например, уравнение
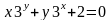 .
Однако и
здесь значениям х
отвечают
определенные значения у
(например,
значению х
=
0 отвечает у
=
-2).
В таких случаях говорят, что
функция у
- неявная функция от
х
, она
задана уравнением, связывающим x
и
у.
Подобным
образом задаются многие кривые в
аналитической геометрии. Например,
.
Однако и
здесь значениям х
отвечают
определенные значения у
(например,
значению х
=
0 отвечает у
=
-2).
В таких случаях говорят, что
функция у
- неявная функция от
х
, она
задана уравнением, связывающим x
и
у.
Подобным
образом задаются многие кривые в
аналитической геометрии. Например,
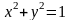 -
уравнение окружности (с центром в начале
координат и радиуса
-
уравнение окружности (с центром в начале
координат и радиуса
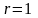 ).
Здесь можно явно выразить у
через
х
:
).
Здесь можно явно выразить у
через
х
:
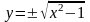 ,
но получаются две
функции, соответствующие "+" или
"-" перед корнем (верхняя и нижняя
полуокружности). Точно
так же уравнение эллипса
,
но получаются две
функции, соответствующие "+" или
"-" перед корнем (верхняя и нижняя
полуокружности). Точно
так же уравнение эллипса
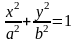 заданием
неявной функции. В самом общем виде
уравнение, задающее неявную функцию,
можно записать как
заданием
неявной функции. В самом общем виде
уравнение, задающее неявную функцию,
можно записать как
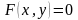
где буква F "скрывает" те операции над х и у, которые следует проделать в основной (левой) части уравнения. Исследовать неявные функции почти всегда труднее.
1.3.4. Параметрическое задание функции. Кривые на плоскости часто задаются параметрическими уравнениями. В этих уравнениях координаты х и у точки на кривой выражены как функции третьего, вспомогательного переменного t (параметра):
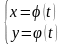
Это
новый, иногда наиболее удобный, способ
задать функциональную зависимость
между х
и
у.
Считаем,
что функция
имеет обратную:
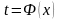 .
[т.е.
решаем уравнение
относительно
].
Поставив это во второе
уравнение, получим:
.
[т.е.
решаем уравнение
относительно
].
Поставив это во второе
уравнение, получим:
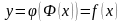
т.е. у есть функция от х (сложная функция).
Примеры:
1)
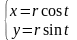
2)
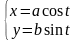
параметрические
уравнения: 1) окружности радиуса
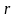 ,
2) эллипса с полуосями а
и
b
.
,
2) эллипса с полуосями а
и
b
.
Весьма часто параметрическое задание линии возникает в механике. Там x и у - координаты движущейся точки, меняющиеся в зависимости от времени t, а линия - траектория этой точки.
