
- •§ 1.1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства
- •Например, матрица a размера 23 записывается в виде:
- •§ 1.2. Миноры и алгебраические дополнения. Разложение
- •§ 1.3. Некоторые виды матриц и их определители
- •§ 1.4. Операции над матрицами. Обратная матрица. Ранг матрицы
- •§ 1.5. Ранг матрицы
- •§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.
- •§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.
- •§1.8. Однородные и неоднородные системы линейных алгебраических
- •Контрольные вопросы
- •Литературы:
- •Лекции № 4-6 Тема 2. Векторная алгебра
- •§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
- •§ 2.2. Простейшие задачи аналитической геометрии
- •§ 2.3. Векторы и линейные операции над ними. Базис векторного
- •§ 2.4. Базис векторного пространства. Координаты вектора
- •Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§ 2.5. Скалярное произведение векторов и его свойства
- •§ 2.6. Векторное произведение векторов и его свойства.
- •§ 2.7. Cмешанное произведение векторов и его свойства
- •Свойства смешанного произведения.
- •Литературы:
- •Глава 5 § 1,2,3,4,5 стр. 110-142
- •Тема 5. Введение в анализ. Функция
- •Множества. Логическая символика
- •Функция. Основные свойства функций
- •Способы задания.
- •1.3.Элементы поведения функции
- •Контрольные вопросы:
- •Глава 3 § 3.1-3.2 стр. 66-85
- •Тема 6. Предел и непрерывность
- •1 Предел переменной величины. Предел последовательности.
- •2.Предел функции Дадим определения пределов функции при
- •3 Бесконечно малые и бесконечно большие функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •3.2 Бесконечно большие функции и их свойства
- •4.Непрерывность функции
- •4.1 Классификация точек разрыва
- •4.2 Свойства функций, непрерывных на отрезке
- •Литературы:
- •Тема 7. Дифференциальное исчисление. Производная
- •Задачи, приводящие к понятию производной
- •1.1 Механический смысл производной. Пусть некоторая точка движется вдоль прямой и за время t проходит путь s(t) (рис.2).
- •1 Дифференцирование сложной функции
- •3. Таблица производных основных элементарных функций
- •4. Параметрически заданная функция и её производная
- •Контрольные вопросы:
- •Тема 8. Дифференциал функции
- •1. Понятие дифференциала функции
- •2 Производные и дифференциалы высших порядков
- •Получаем формулы для вычисления такого дифференциала:
- •3. Приложения производной
- •1. Основные теоремы дифференциального исчисления
- •2 Правило Лопиталя
- •Контрольные вопросы:
- •Литература:
- •Тема 9 Исследование поведения функции и их графиков.
- •Для этого определим интервалы знакопостоянства ее производной
- •Выпуклость и точки перегиба
- •Асимптоты графика функции
- •Контрольные вопросы:
- •Литература:
Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор в пространстве записывают в виде:
=(x,y,z) или ={x,y,z}
Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
Пусть в пространстве имеется декартова система координат Oxyz. С ней связан стандартный базис из единичных взаимно перпендикулярных векторов, расположенных вдоль осей Ox, Oy, Oz. Эти
базисные век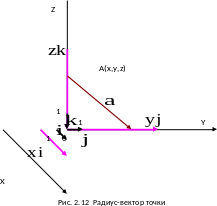 тора
обозначаются через
тора
обозначаются через
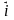 ,
,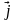 ,
,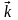 .
.
Выясним связь между введёнными ранее понятиями координат точки в системе Oxyz и вектора в базисе { , , }.
Определение. Вектор, начало которого находится в начале координат, а конец в точке A, т.е. вектор , называется радиус–вектором точки A.
Если (x,y,z) – координаты точки A в системе Oxyz, то радиус–вектор можно записать в виде =x +y +z . Поэтому координаты точки A(x,y,z) в системе Oxyz и вектора в базисе { , , } – это одни и те же числа.
Теорема.
Пусть в
декартовой системе координат Oxyz
заданы две точки A(xA,yA,zA)
и B(xB,yB,zB),
тогда в базисе {
,
,
}
вектор
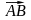 имеет координаты ((xВ–
xА),(yВ–yА),(zВ–zА)).
имеет координаты ((xВ–
xА),(yВ–yА),(zВ–zА)).
Доказательство. Запишем вектор в виде:
=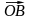 –
=
+(–1)
–
=
+(–1)
и воспользуемся
результатом предыдущей теоремы для
базиса {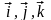 },
получим:
},
получим:
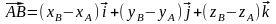 .
.
Пример3. Пусть A(1,–1,1), B(2,3,4), тогда в базисе { , , }
=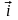 +4
+4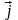 +3
+3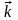 ,
т.е.
={1,4,3}.
,
т.е.
={1,4,3}.
Иногда координаты вектора в базисе { , , } удобно представлять себе в виде проекций.
Определение. Проекцией вектора на координатную ось L называется длина проекции вектора на L, взятая со знаком “+”, если угол между и положительным направлением оси острый, и “–“, если он тупой.
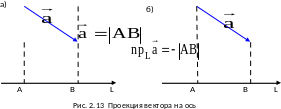
При параллельном
переносе вектора, его проекция на ось
L
не меняется. Проекция обозначается
символами
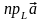 .
Несложно проверить, что
.
Несложно проверить, что
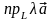 =
=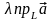 и
и
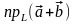 =
+
=
+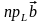 .
Очевидно, что если
имеет координаты
.
Очевидно, что если
имеет координаты
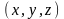 то
то
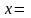
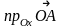 ,
,
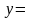
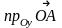 ,
,
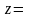
 .
.
Отсюда получим следующую теорему.
Теорема.
Пусть вектор
имеет координаты
 в базисе
в базисе
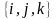 ,
тогда
,
тогда
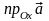 ,
,
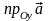 ,
,
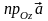 .
.
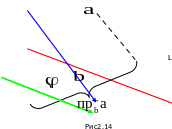
Определение.
Проекцией
вектора
на
ненулевой вектор
(обозначение
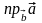 )
называется его проекция на ось L,
проведенная через вектор
(см. рис. 2.14).
)
называется его проекция на ось L,
проведенная через вектор
(см. рис. 2.14).
§ 2.5. Скалярное произведение векторов и его свойства
Имеются три вида произведений векторов: скалярное, векторное и смешанное. Название первого из них произошло от слова скаляр – число. Скалярная величина в математике – это величина, принимающая численные значения.
Определение. Скалярным произведением векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними, т. е.
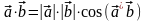 .
.
Скалярное
произведение обозначается символами
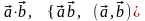 .
.
Пример 1. Если
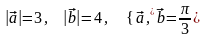 ,
то
,
то
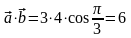 .
.
Пример 2. Пусть
точка перемещается вдоль вектора
под действием постоянной силы
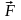 ,
соста
,
соста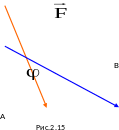 вляющей
угол
вляющей
угол
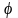 с отрезком
(см. рис. 2.15).
с отрезком
(см. рис. 2.15).
Тогда из механики известно, что работа этой силы по перемещению точки равна скалярному произведению векторов и , т.е.
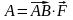 .
.
Свойства скалярного произведения
10
Для любых
векторов
и
:
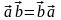 ,
т.е. это произведение коммутативно.
,
т.е. это произведение коммутативно.
20 Для любого вектора :
.
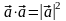 .
.
30
Скалярные
произведение ненулевых векторов
и
равно
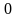 только в том случае, когда эти векторы
ортогональны (перпендикулярны).
только в том случае, когда эти векторы
ортогональны (перпендикулярны).
40 Для любых векторов и верно соотношение
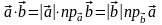 .
.
50
Для любого
вектора
с координатами
в базисе
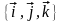 верно
верно
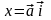 ,
,
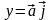 ,
,
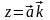 .
.
60 Постоянный множитель можно выносить за знак скалярного произведения, т.е. для любых векторов , и числа верно:
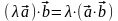 .
.
70
Cкалярное
произведение обладает свойством
дистрибутивности, т.е. для любых векторов
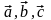 :
:
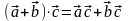 .
.
Следствие.
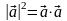
Пример3. Найдем
длину большей диагонали
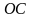 параллелограмма, образованного векторами
и
,
если
параллелограмма, образованного векторами
и
,
если
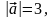
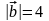 ,
,
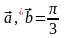 (
( см.
рис. 2.16).
см.
рис. 2.16).
Поскольку
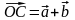 ,
то
,
то
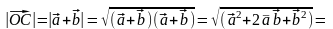
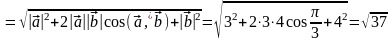 .
.
Получим формулу для вычисления скалярного произведения в случае, когда векторы заданы своими координатами, а также некоторые следствия из нее. Для определенности будем считать, что все векторы определены в пространстве. Для случая плоскости во всех формулах следует отбросить аппликаты всех векторов (координату ).
Теорема. Пусть
в базисе
вектор
имеет координаты
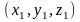 ,
а вектор
–
,
а вектор
–
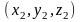 .
Тогда
.
Тогда
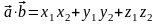 .
.
Доказательство. Воспользуемся свойствами 6 и 7 скалярного произведения, получим
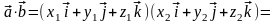
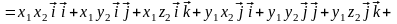
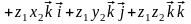 .
.
Поскольку базисные
векторы
взаимно перпендикулярны, то
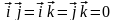 ,
а поскольку эти векторы имеют единичную
длину, то
,
а поскольку эти векторы имеют единичную
длину, то
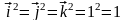 .
Подставив эти соотношения в последнее
равенство, получим, что
.
Подставив эти соотношения в последнее
равенство, получим, что
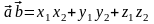 .
.
Пример4. Если
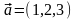 ,
а
,
а
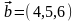 ,
то
,
то
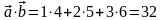 .
.
Следствие
1. Если
вектор
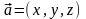 ,
в базисе
,
то
,
в базисе
,
то
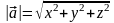 .
.
Доказательство.
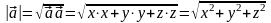 .
.
Пример5. Если , то
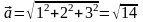 .
.
Следствие 2.
Косинус угла
между векторами
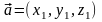 и
и
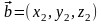 равен:
равен:
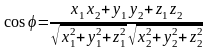 .
.
Доказательство.
Из соотношения
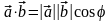 получим
получим
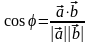 .
Затем для вычисления
.
Затем для вычисления
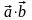 воспользуемся теоремой, а для
воспользуемся теоремой, а для
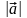 и
и
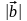
следствием 1.
Пример6. Если , , то
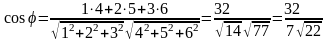 .
.
Следствие 3. Векторы и перпендикулярны только в том случае, когда
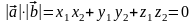 .
.
Определение.
Направляющими
косинусами
ненулевого вектора
называются косинусы углов, образованных
этим вектором с осями координат
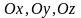 (см. рис. 2.17).
(см. рис. 2.17).
Обычно эти углы
обозначаются через
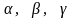 .
.
Следствие 4. Для вектора с координатами направляющие косинусы записываются в виде:
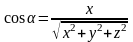 ;
;
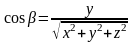 ;
;
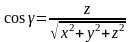 .
.
Доказательство.
Поскольку
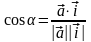 ,
то учитывая, что
,
то учитывая, что
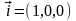 из следствия 2 будем иметь:
из следствия 2 будем иметь:
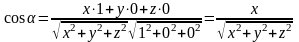 .
.
Остальные формулы доказываются аналогично.

Пример 7.
Если
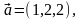 то
то
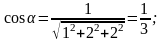
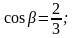
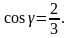
Направляющие косинусы вектора обладают следующим свойством.
Следствие 5.
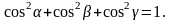
Доказательство. Из предыдущего следствия получим:
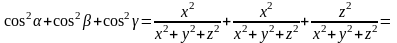
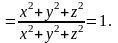
Определение. Вектор координаты которого совпадают с
направляющими косинусами вектора , называется ортом вектора .
Его обозначение
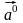 =(
=(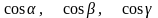 ).
).
Орт вектора по модулю равен 1 и сонаправлен вектору .
В самом деле из
следствия и следует
что
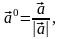 т.е.
коллинеарен
и имеет то же направление.
т.е.
коллинеарен
и имеет то же направление.
Пример 8.
Для вектора
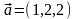 :
:
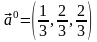 .
.
