
- •Часть 1. Исследование систем счисления и методов конвертирования
- •Часть 2. Кодирование данных в микропроцессорной технике
- •Часть 3. Арифметические операции при обработке данных
- •Лабораторная работа №1. Основы машинной арифметики.
- •Часть 1. Исследование систем счисления и методов конвертирования
- •Содержание отчета
- •1. Введение в системы счисления
- •1.1 Общие положения. Классификация систем счисления
- •1.2 Позиционные системы счисления. Полиномиальное представление чисел
- •1.3 Системы счисления, применяемые в микропроцессорной
- •1.4 Некоторые свойства позиционных однородных систем с естественным множеством цифр
- •2. Преобразование чисел из одной системы счисления в другую
- •2.1 Методы конвертирования
- •2.2 Метод подбора
- •2.3 Метод замещения полиномиальных элементов (поэлементное замещение)
- •2.4 Метод, основанный на “схеме Горнера”
- •2.5 Метод “цифра за цифрой”
- •2.5.1 Конверсия целого числа методом “цифра за цифрой”
- •2.5.2 Конверсия дробного числа методом “цифра за цифрой”
- •2.6 Методы, учитывающие специфические соотношения оснований систем счисления
- •2.6.1 Двоично-шестнадцатеричные и шестнадцатерично-двоичные преобразования
- •2.6.2 Двоично-восьмеричные и восьмерично-двоичные преобразования
- •2.7 Методы, использующие промежуточные системы систем счисления
- •Часть 2. Кодирование данных в микропроцессорной технике
- •2. Теоретические основы кодирования чисел
- •3. Обратные коды двоичных чисел.
- •Дополнительные коды числовых данных
- •Часть 3. Арифметические операции при обработке данных
- •1. Предварительные замечания
- •3.1.1. Сложение дробных и целых положительных чисел без переполнения. (Случай 1)
- •3.1.2. Сложение дробных и целых положительных чисел с переполнением (Случай 2)
- •3.1.3. Сложение дробных и целых отрицательных чисел без переполнения (Случай 3)
- •3.1.4. Сложение дробных и целых отрицательных чисел с переполнением (Случай 4)
- •3.1.5. Сложение отрицательных чисел с “особым случаем переполнения”(Случай 5)
- •3.6.Сложение чисел разных знаков
- •3.1.6.1. Модуль положительного операнда больше модуля отрицательного. (Случаи 6, 9)
- •3.1.6.3. Модуль положительного операнда меньше модуля отрицательного (Случаи 7,8).
- •3.1.7 Обнаружение переполнения разрядной сетки в пдк
- •3.2.1. Сложение в обратных кодах дробных и целых отрицательных чисел без переполнения (Случай 3ок)
- •3.1.4. Сложение в обратных кодах дробных и целых отрицательных чисел с переполнением (Случай 4ок)
- •3.1.5. Сложение в обратных кодах отрицательных чисел с “особым случаем переполнением ” при сложении в дополнительных кодах (Случай 5)
- •3.1.6.Сложение в обратных кодах чисел разных знаков
- •3.1.6.1. Модуль положительного операнда больше модуля отрицательного. (Случаи 6, 9)
- •3.4 Обнаружение переполнения разрядной сетки в пок
- •4. Cложение чисел в модифицированных дополнительных кодах (мдк)
- •4.2.1. Сложение дробных и целых положительных чисел без переполнения. (Случай 1)
- •3.2.2. Сложение дробных и целых положительных чисел с переполнением (Случай 2)
- •3.2.3. Сложение дробных и целых отрицательных чисел без переполнения (Случай 3)
- •3.2.4. Сложение дробных и целых отрицательных чисел с переполнением (Случай 4)
- •3.2.5. Сложение целых отрицательных чисел с “особым случаем переполнения”(Случай 5)
- •3.2.6.Сложение чисел разного знака в модифицированных дополнительных кодах
- •3.2.6.1. Модуль положительного операнда больше модуля отрицательного. (Случаи 6,9)
- •3.2.6.3. Модуль положительного операнда меньше модуля отрицательного (Случаи 7,8).
- •4. Обнаружение переполнения разрядной сетки в модифицированных дополнительных кодах
Часть 3. Арифметические операции при обработке данных
Цель работы. Изучить простейшие арифметические операции, используемые в микропроцессорной технике. К таким, часто встречающимся операциям, относятся операции: сложение/вычитание в прямых/ модифицированных, простых/ обратных/ дополнительных кодах.
Знать особенности выполнения каждой операции.
Необходимо учесть, что изучаемый материал является базовым для последующих лабораторных работ, а также включается в виде теоретических вопросов и заданий (задач) в экзаменационные билеты.
Порядок выполнения.
Изучить теоретические основы операций над числовыми данными (Приложение. Теоретические основы кодирования).
Выполнить заданные примеры.
Пример индивидуального задания
Заданные числа и результат представить прямыми двоич ными кодами с количеством числовых разрядов - 7.
1. Вычесть (A-B) с фиксированной запятой в модифицированных
дополнительных двоичных кодах следующие числа:
A = -0.2968750 B = -0.4531250
A = -0.8593750 B = 0.1406250
2. Сложить (A+B) с фиксированной запятой в простых
обратных двоичных кодах следующие числа:
A = 0.3671875 B = -0.7109375
A = 0.3671875 B = 0.7500000
В методических указаниях излагаются теоретические основы базовой для вычислительной и микропроцессорной техники операции – операции сложения.
1. Предварительные замечания
1.1. Основным узлом информационных систем, осуществляющим арифметические операции, является сумматор с базовой функцией суммирования.
Через такую операцию реализуются другие арифметические операции, а именно
операция вычитания, интерпретируемая как операция сложения отрицательных операндов, представляемых в виде обратных или дополнительных кодов;
операция умножения, интерпретируемая как последовательность операций сдвигов множимого/множителя и сложений, обеспечивающих накопление суммы частичных (промежуточных) произведений;
операция деления, интерпретируемая как последовательность операций вычитания (сложения делимого в дополнительном коде) с формированием очередной цифры частного
и т.д.
Функцию суммирования выполняет комбинационная схема, функционирование i–го разряда которой описывается таблицей соответствия (ТС) вида:
В таблице использованы следующие
обозначения:
таблице использованы следующие
обозначения:
CI (carry input) перенос из предыдущего разряда, влияющий на значение формируемой суммы s;
CO (carry out) перенос в следующий разряд, возникающий при суммировании.
Таблицей описывается правило формирования одного разряда суммы s, учитывающее значения (биты) a, b слагаемых и бит переноса (СI) из младшего разряда. Кроме того, ТС задает правило формирования бита переноса CO в следующий разряд суммы.
Поэтому такой сумматор наз. полным одноразрядным комбинационным сумматором.
И![]() з
таблицы можно получить нормальные формы
функций суммы s
и переноса CO,
которые после упрощения представляются
в виде:
з
таблицы можно получить нормальные формы
функций суммы s
и переноса CO,
которые после упрощения представляются
в виде:
Н![]()
 а
рисунке 1 приведена схема одноразрядного
полного комбинационного сумматора,
соответствующего выражениям (1),(2).
а
рисунке 1 приведена схема одноразрядного
полного комбинационного сумматора,
соответствующего выражениям (1),(2).
Одноразрядные сумматоры составляют основу для построения n–разрядных сумматоров, обеспечивающих сложение n – разрядных операндов (слагаемых).
На рисунках 2 и 3 приведены функциональные схемы n–разрядных сумматоров обратного и дополнительного кодов.
 В
сумматоре дополнительного кода
отсутствует связь циклического переноса
из старшего (знакового) разряда в младший
разряд. Это схемотехнически обеспечивает
преимущества суммирования в дополнительных
кодах. Сумматоры дополнительного кода
являются основными функциональными
частями арифметико–логических устройств
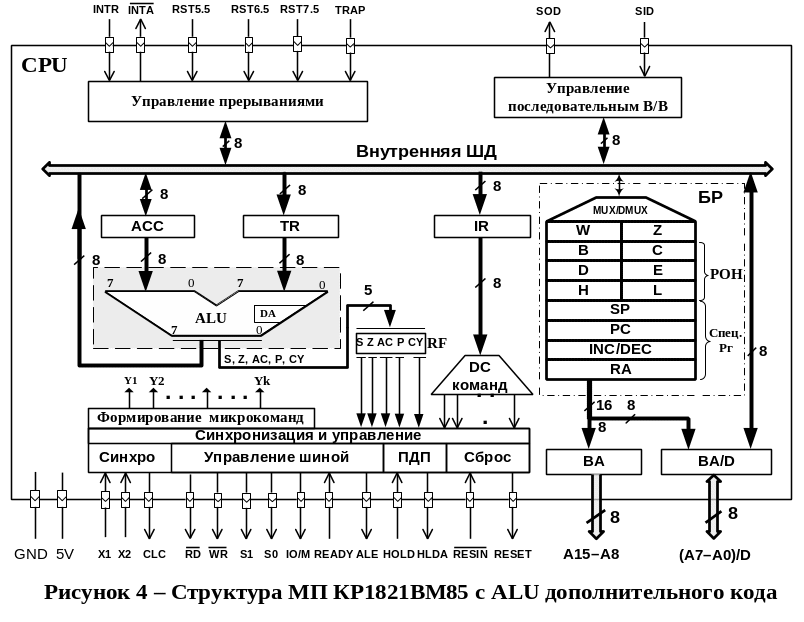
(АЛУ) современных микропроцессоров. На
рисунке 4 выделен восьмиразрядный
сумматор дополнительного кода,
используемый как основной блок АЛУ
процессора I8085
(К1821ВМ85).
В
сумматоре дополнительного кода
отсутствует связь циклического переноса
из старшего (знакового) разряда в младший
разряд. Это схемотехнически обеспечивает
преимущества суммирования в дополнительных
кодах. Сумматоры дополнительного кода
являются основными функциональными
частями арифметико–логических устройств
(АЛУ) современных микропроцессоров. На
рисунке 4 выделен восьмиразрядный
сумматор дополнительного кода,
используемый как основной блок АЛУ
процессора I8085
(К1821ВМ85).
Применяя одноразрядные сумматоры в качестве базовых элементов, можно реализовать сумматоры, обеспечивающие сложение двух и более операндов любой разрядности.
П ример
1
Выполнить
сложение двух положительных восьмиразрядных
двоичных чисел [A]пр=0.0001010
и [B]пр=0.0001110
ример
1
Выполнить
сложение двух положительных восьмиразрядных
двоичных чисел [A]пр=0.0001010
и [B]пр=0.0001110
Пример показывает, что сложение двух положительных чисел может быть выполнено непосредственно в прямых кодах. Проблемы возникают при обработке отрицательных операндов. Пути разрешения такой проблемы будут обсуждаться далее.
1.2 При сложении чисел необходимо учитывать форму их представления. Они могут складываться или как целые или как дробные числа. Такое представление наз. представлением в форме с фиксированной запятой.
Представление с ФЗ широко используется в МПТ.
В этом формате в машинном коде числа запятой как символа – нет, однако, её положения известно “по умолчанию ”.
О бычно
подразумевается, что запятая находится
или после младшего разряда значащей
части числа или перед её старшим разрядом
(после знакового).
бычно
подразумевается, что запятая находится
или после младшего разряда значащей
части числа или перед её старшим разрядом
(после знакового).
В первом случае без изменения (по сравнению с исходными) могут быть представлены только целые числа, во втором — только дробные, т.е. числа, модуль которых не превосходит 1.
На рис.5 показан пример разрядной сетки ИС («формат данных») для представления двоичных чисел с фиксированной запятой в виде n-разрядного слова для случаев закрепления запятой после младшего разряда (формат а)) и (m+1)–разрядного слова для случаев закрепления запятой после знакового разряда(формат б)).
В формате с ФЗ старший разряд кода числа содержит один разряд кода знака (S- signum), остальные разряды кода числа – значащие, т.е. используются для представления кода модуля числа.
1.3. Применяя при сложении форматы с фиксированной запятой необходимо контролировать диапазон допустимых модулей суммы чисел.
Если результат операции превышает Xмакс– т.е. максимально представимое в заданной разрядной сетке и в используемом формате число, то возникает т.н. переполнение. Дальнейшее выполнение программы при переполнении не имеет смысла.
При известных длинах разрядной сетки можно определить диапазоны представимых в форме с фиксированной запятой сумм.
Очевидно, что поддиапазоны положительных и отрицательных чисел симметричны относительно истинного нуля. Поэтому дальнейший анализ может быть выполнен для модулей представляемых чисел.
Дробные числа.
Максимальное по модулю положительное или отрицательное число содержит во всех значащих разрядах единицы и отличается от 1 на единицу младшего разряда.
Пример 2. Пусть m =7. Тогда |Xмакс| =0.1111111. Подсуммирование единицы в младший разряд приводит к результату: 0,1111111 + 0.0000001 =1,0000000. Сумма равна единице, которая выходит за формат дробных чисел.
С![]() праведливо
праведливо
В формуле (3): m – номер младшего разряда машинного слова (Рис.5)
Таким образом, переполнение разрядной сетки при сложении дробных чисел описывается условиями

Целые числа.
Максимальное по модулю положительное или отрицательное целое число содержит во всех значащих разрядах единицы.
П![]() оэтому
справедливо
оэтому
справедливо
С учетом (5), переполнение разрядной сетки при сложении целых чисел описывается условиями
![]() Из
соотношений (3) и (6) вытекают следующие
определения.
Из
соотношений (3) и (6) вытекают следующие
определения.
Переполнение разрядной сетки – случай при сложении, когда модуль суммы превышает максимальное число, представимое в заданной разрядной сетке;
Переполнение возможно только при сложении чисел одного знака, так как модуль суммы в этом случае всегда превышает модули ненулевых слагаемых;
Переполнение невозможно при сложении чисел разных знаков. Модуль суммы в этом случае меньше модуля максимального и представимого в заданной разрядной сетке слагаемого;
Переполнение, возникающее при сложении двух отрицательных операндов наз. отрицательным переполнением, а переполнение, возникающее при сложении двух положительных операндов – положительным.
3. Сложение чисел в простых кодах
Следует различать процедуры сложения в простых и модифицированных кодах.
В простых кодах для кодирования знака используется один старший разряд кода.
В модифицированных кодах для кодирования знака используется два разряда кода.
Ниже, в этом разделе рассматриваются особенности сложения в простых дополнительных и обратных кодах, а затем в разделе 4 сложение в модифицированных кодах.
3.1. Процедура сложения чисел в простых дополнительных кодах (ПДК)
Процедура1. Основные правила сложения в простых дополнительных кодах:
положительные операнды участвуют в сложении в прямых кодах;
отрицательные операнды должны быть преобразованы в дополнительные коды и, в таком виде – суммироваться;
знаковый разряд слагаемых участвует в операции наравне с числовыми разрядами;
перенос из знакового разряда, который может возникнуть при сложении, должен быть игнорирован (отброшен);
при суммировании операндов одного знака возможно отрицательное или положительное переполнение;
при сложении может формироваться либо положительная, либо отрицательная сумма. При этом:
6.1 если сумма – положительное число, а переполнение отсутствует, то она содержит “0” в знаковом разряде и представлена в прямом коде.
6.2 если сумма – отрицательна, то результат суммирования содержит единицу в знаковом разряде, а сумма представлена в дополнительном коде;
при использовании дополнительных кодов возможен случай т.н. особого переполнения (особый случай переполнения).
Далее проводится анализ различных случаев сложения (Процедура 1) в дополнительных простых кодах чисел, представленных в форматах дробных и целых чисел. Таблица 1, строится исходя из того, что на результаты сложения влияют
знаки слагаемых;
величины модулей слагаемых и их соотношение.
Учитывается то, что при сложении возможно переполнение результата, определяются признаки таких ситуаций. Выделены по перечисленным признакам девять случаев, которые могут иметь место при сложении. В последующий разделах каждый случай проанализирован с точки зрения возможности его возникновения, особенностей получаемых результатов и последствий.
