2. Теоретические основы кодирования чисел

Обратные и дополнительные коды предполагают изменение значащей части отрицательного числа. Такое изменение выполняется с целью замены операции вычитания чисел операцией сложения.

Аналитическим решением, позволяющим заменить операцию вычитания сложением является замена отрицательных операндов особого рода числами ( кодами).

Пусть из положительного операнда A требуется вычесть положительный операнд B или прибавить отрицательный операнд (–В).

Принципиальная возможность замены вычитания операцией сложения следует из следующего алгебраического выражения

В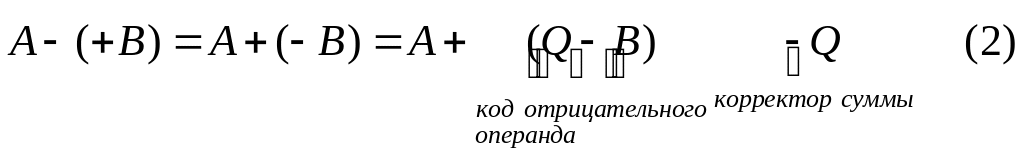 этом выражении Q –некоторое значение (параметр), использование которого позволяет перейти к кодам (Q–B) отрицательных операндов. а затем, при необходимости, откорректировать полученную сумму (вычитание Q в правой части (2)).

Анализ выражения 2 позволяет сформулировать в общем виде требования к параметру Q:

1. для положительного числа B и операции сложения параметр Q должен принимать нулевое значение

1. параметр Q для отрицательного операнда должен быть постоянной положительной величиной, не зависящей от значения модуля операнда;

2. если Bмакс – максимальное значение модуля операнда, то должно выполняться соотношение ;

3. выбор Q должен предполагать возможность замены операции вычесть (Q–B) при образовании кода типовыми логическими операциями и операцией сложения;

4. выбор Q должен обеспечить операцию коррекции (–Q), не связанную с вычитанием.

5. Требования достаточно противоречивы, однако, выполнимы.

Теоретические исследования позволили предложить несколько значений параметра Q, каждый из которых определяет тип кода со специфическими свойствами.

Коды, образованные параметрами Q= 2ⁿ –1 и Q= 2– 2^–m называются обратными кодами, соответственно целых и дробных двоичных чисел. Коды, образованные параметрами Q= 2ⁿ и q= 2 называются дополнительными кодами, соответственно целых и дробных двоичных чисел.

3. Обратные коды двоичных чисел.

3.1 Прямые преобразования

Прямыми называются преобразования из прямого кода в обратный.

Обратные коды двоичных чисел задаются двумя соотношениями

д ля положительных чисел:

для отрицательных чисел:

В ыражение (3а) получается, если принять в алгебраическом выражении (2) значение параметра Q равным 0, выполняя тем самым требование 1.

Выражение (3б) задает обратный код отрицательного числа в аналитическом виде и в полном соответствии с (2).

Пример4. Используя аналитическую зависимость 3б получить обратный код отрицательного числа [A]_пр=10001010 из примера 3

Решение.

Число [A]_пр=10001010–целое. Его модуль равен

|A| =0 0001010.

П оследовательность вычитаний: сначала 2ⁿ –|A|, а затем вычитание из полученной разности 1 приводит к результату

Пример иллюстрирует то обстоятельство, что непосредственное получение кода по выражениям 3 требует двух арифметических операций вычитания, что противоречит требованию 4.

Поэтому целесообразен переход к следующей логической процедуре.

Процедура 2.

Для получения обратного кода отрицательного дробного или целого чисел заданных в прямом коде, необходимо:

1. сохранить значение знакового разряда прямого кода;

2. выполнить поразрядную инверсию значащей части прямого кода числа. Поразрядная инверсия выполняется путем замены в каждом разряде нулевого значения на единичное и единичного на нулевое.

Справедливость процедуры доказывается следующим образом.

Пусть задано n–разрядное целое отрицательное число. Для упрощения, пусть n=8 (это не приводит потери общности).

Первое. Изменив порядок вычитаний, а именно, сначала находя разность 2ⁿ –1 , нетрудно получить

При втором вычитании целесообразно учесть также логическое тождество . Тогда

С вязь исходного операнда и его обратного кода очевидна. Она иллюстрируется диаграммой

Сопоставление левой и правой части диаграммы позволяют сделать следующие выводы: выполненные преобразования ( два последовательных вычитания) не затрагивают (сохраняют) знак исходного операнда, и сводятся в итоге к поразрядной инверсии его мантиссы. Это доказывает справедливость Процедуры 2.

Пример 5. Представить в обратном коде отрицательные числа

[A]_пр=10001010 и [B]_пр=1.0001110.

Решение. [A]_обр=11110101 и [B]_обр=1.11100011

Процедура 1 инвариантна к формату преобразуемого операнда – целое или дробное число с фиксированной запятой.

Аналитически подтвердить справедливость Процедуры 2применительно к дробным числам можно следующим образом.

Пусть задано (m+1)–разрядное дробное число. Как и ранее, сначала определяется разность 2 –2^–m.

В ычитая из полученной разности модуль преобразуемого в код дробного операнда, можно получить его обратный код , в виде разности

К ак и ранее, преобразования через вычитания не затрагивают (сохраняют) знак исходного операнда, и сводятся к поразрядной инверсии его дробной части. Это доказывает справедливость Процедуры 2 для дробных чисел.

Целесообразно выделить следующее свойство обратных кодов, получаемых с помощью выражения (3).

Модуль обратного кода отрицательного числа X – это алгебраическое дополнение модуля кодируемого числа до максимального числа, представимого в разрядной сетке заданного формата.

Д ействительно, модуль максимального представимого в заданном формате целого или дробного числа характеризуется наличием единиц во всех числовых разрядах.

Именно к этому результату можно прийти, выполнив сложение

3.2 Обратные преобразования

Обратными преобразованиями наз. преобразования, обеспечивающие получение из обратного кода прямого.

Для перевода из обратного в прямой код при отрицательной сумме выполняется следующая процедура.

Процедура 3. Для преобразования обратного кода отрицательного числа в прямой код необходимо

1. сохранить знак обратного кода;

2. выполнить поразрядную инверсию значащей части обратного кода.

Процедура справедлива для формата целых и дробных чисел.

Процедура вытекает из ранее доказанных соотношений и в аналитическом виде описывается как

а) для целых чисел

б) для дробных чисел

Пример 6. Преобразовать в прямые коды следующие числа, представленные в обратных кодах.

Решение. Исходные данные и результаты преобразований представлены в таблице.

Обратные коды чисел	Прямые коды, полученные после преобразования
1.0011110B	1. 1100001B
01101001B	01101001B
1.0011001B	1.1100110B
0.1111001B	0.1111001B

Недостатком обратных кодов является необходимость подсуммирования переноса из знакового разряда суммы к младшему разряду суммы. Это усложняет сумматор и требует дополнительных затрат машинного времени.