3.4 Уравнение прямой с угловым коэффициентом и некоторые другие уравнения прямой на плоскости
1. Пусть, в общем уравнении прямой
коэффициент
,
тогда разрешая это уравнение относительно
,
получим
.
Обозначаем
,
,
тогда получим уравнение прямой, которое
называется уравнением прямой с
угловым коэффициентом:
,
здесь
- угловой коэффициент прямой -
равен тангенсу угла наклона прямой к
оси абсцисс, коэффициент
- ордината точки пересечения прямой
с осью ординат.
2. Предположим теперь, что прямая
проходит через точку
.
Тогда
,
и, вычитая почленно из уравнения прямой
полученное равенство, получим уравнение
прямой с заданным угловым коэффициентом,
проходящее через точку
.
Иногда говорят, уравнение пучка прямых,
проходящих через т.
.
3. Если прямая проходит через две
заданные точки
и
,
то, подставляя в последнее уравнение
координаты точки
и, исключая из обоих уравнений угловой
коэффициент, получим уравнение прямой,
проходящей через две заданные точки
.
4. Если в общем, уравнении прямой
коэффициенты
не равны нулю, то уравнение можно
переписать в виде
или
.
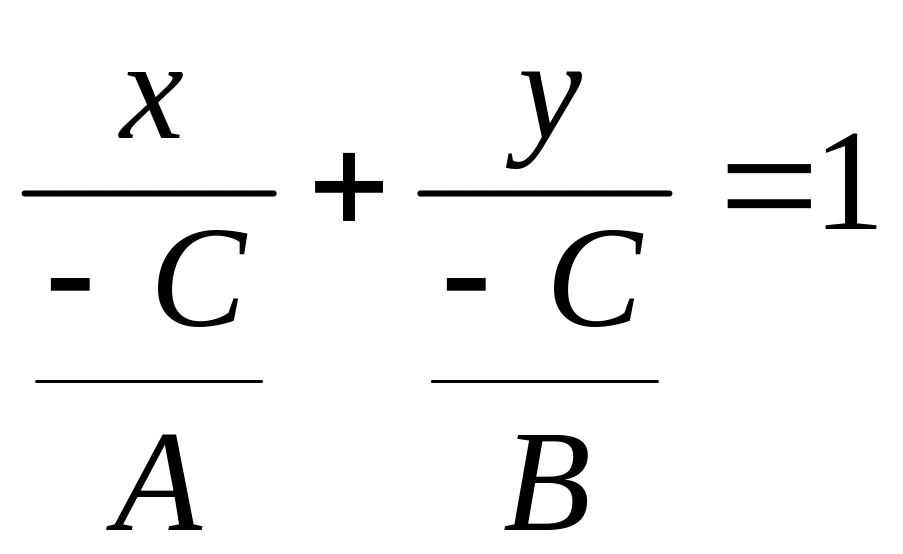Обозначив
,
,
получим уравнение прямой в отрезках:
,
здесь
и
отрезки (с соответствующим знаком),
которые отсекает прямая на осях координат.
5. Любой вектор
параллельный данной прямой назовем
направляющим вектором прямой.
Если, кроме этого, на прямой задана точка
,
то произвольная точка
лежит на прямой тогда и только тогда,
когда вектор
коллинеарен направляющему вектору
.
Условие коллинеарности и дает уравнение
прямой, проходящей через фиксированную
точку с заданным направляющим вектором:
.
Пример 1. Написать уравнение прямой
проходящей через точки
,
.
Решение. Используя уравнение прямой,
проходящей через две точки, получим
.
Пример
2. Построить прямую
на плоскости, найти угловой коэффициент
прямой.
Решение.
1). Запишем уравнение прямой
в отрезках. Для этого разделим обе
части уравнения на 12, получим
.
Видим, что прямая отсекает на оси
отрезок
,
на оси
отрезок
.
2) Выразим из уравнения прямой :
.
Видим, что угловой коэффициент
,
т.е.
.
3.5. Взаимное расположение прямых на плоскости
Пусть две различные прямые на плоскости
заданы своими общими уравнениями
и
.
Положение каждой из них полностью
определяется координатами любой точки
на прямой и нормальным вектором этой
прямой. Первая прямая имеет нормальный
вектор
,
вторая -
.
Очевидно, что взаимное расположение
этих прямых полностью определяется
их нормальными векторами.
Прямые
и
параллельны, если векторы
и
коллинеарны, то есть существует скаляр
λ такой, что
или
.
Прямые
и
перпендикулярны, если векторы
и
перпендикулярны, то есть их скалярное
произведение равно нулю
или
.
Один из смежных углов
между двумя прямыми
и
определяется как угол между векторами
и
известной формулой
.
Если же эти прямые заданы уравнениями
с угловыми коэффициентами
и
,
то угол между прямыми определяется
формулой
,
которая является прямым следствием
тригонометрической зависимости
.
Отсюда сразу же следуют условие
параллельности
и условие перпендикулярности
прямых.
Пример. Написать уравнение прямой,
проходящей через точку
параллельно прямой
и найти проекцию этой точки на данную
прямую.
Решение. Поскольку искомая прямая
параллельна данной, то за ее нормальный
вектор можно взять вектор
- перпендикулярный заданной прямой.
Тогда уравнение параллельной прямой
или
.
Проекцию точки на прямую можно найти
как пересечение заданной прямой и
перпендикулярной к ней. Заметим, что
нормальный вектор
заданной прямой является одновременно
направляющим вектором
искомого перпендикуляра, значит,
уравнение этого перпендикуляра имеет
вид
,
или, после несложных преобразований
получаем общее уравнение перпендикулярной
прямой
.
В заключение ищем координаты точки
пересечения двух прямых, для этого
решаем систему уравнений:
Умножаем первое уравнение на 3, а второе
на 7 и складываем, в результате получим
,
откуда
.
Исключая переменную
,
найдем
.
Итак, проекция точки на прямую есть
точка
.