1.8. Ранг матрицы
Рассмотрим произвольную матрицу размера m на n
A=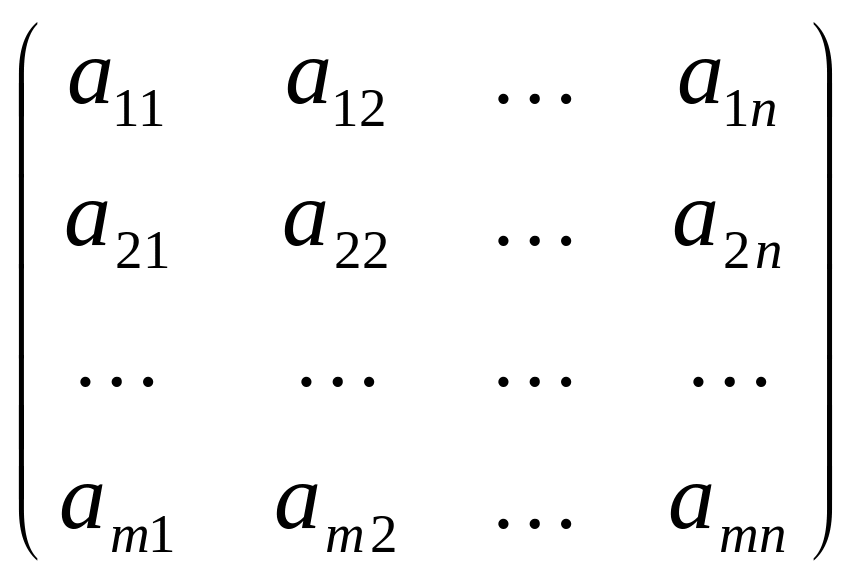
.
Выделим в этой матрице произвольным образом к строк и к столбцов. Элементы, которые находятся на пересечении выделенных строк и столбцов, образуют квадратную матрицу к-ого порядка.
Определение. Минором к-ого порядка матрицы А называется определитель составленный из элементов матрицы, лежащих на пересечении любых к строк и к столбцов.
Например, матрица
имеет 9 миноров первого порядка – это
элементы матрицы 2, 5, 1, 0, 7, 0, 4, 10, 2. Отметим,
что среди миноров первого порядка
имеются отличные от нуля. Выпишем все
миноры второго порядка.
Замечаем, что среди миноров второго порядка также есть отличные от нуля.
Последний минор нашей матрицы –
определитель самой матрицы
.
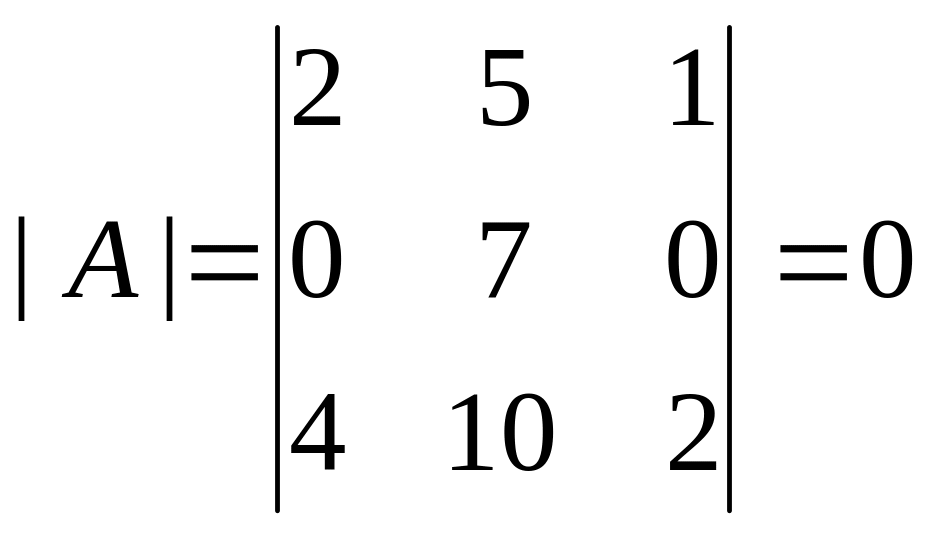То есть единственный минор третьего
порядка равен нулю.
Таким образом, максимальный порядок минора отличного от нуля равен двум. В этом случае говорят, что ранг матрицы А равен 2.
Определение. Наибольший из порядков миноров матрицы А отличных от нуля называется рангом матрицы А. В этом случае принято писать: rang A=r . Например, в рассмотренном примере, rang A=2.
При нахождении ранга матрицы следует иметь в виду достаточно очевидный факт: если все миноры порядка r+1 матрицы А равны нулю, то и все миноры более высоких порядков также равны нулю.
Понятие ранга матрицы играет принципиальную роль при исследовании систем линейных уравнений.
2. Системы линейных алгебраических уравнений - слау
2.1 Основные определения
Определение. Системой m
линейных алгебраических уравнений
с
неизвестными
назовем систему вида
Здесь
,
i=1,…,m;
j=1,…,n
- коэффициенты системы, и
,
i=1,…,m
- свободные члены системы –
заданные числа.
Решением системы назовем любой
набор
чисел
(
),
который, будучи подставлен в систему,
обращает все уравнения системы в верные
равенства.
Система, которая имеет хотя бы одно решение, называется совместной, если это решение единственное – определенной, более одного решения – неопределенной. Система, не имеющая решений, называется несовместной.
Как и в случае систем двух линейных уравнений с двумя неизвестными, произвольная СЛАУ m уравнений с n неизвестными полностью определяется главной матрицей системы А , столбцом свободных членов В и столбцом неизвестных Х:
, 
, 
.
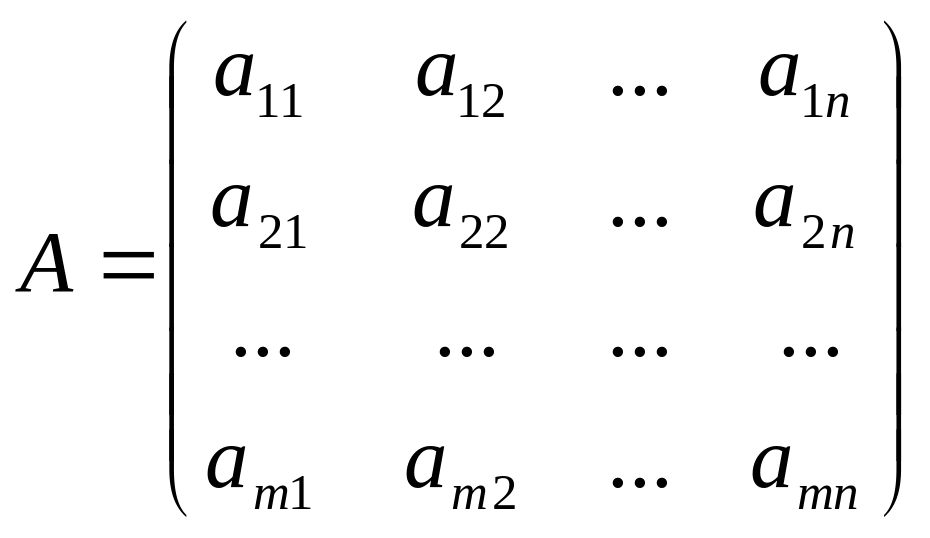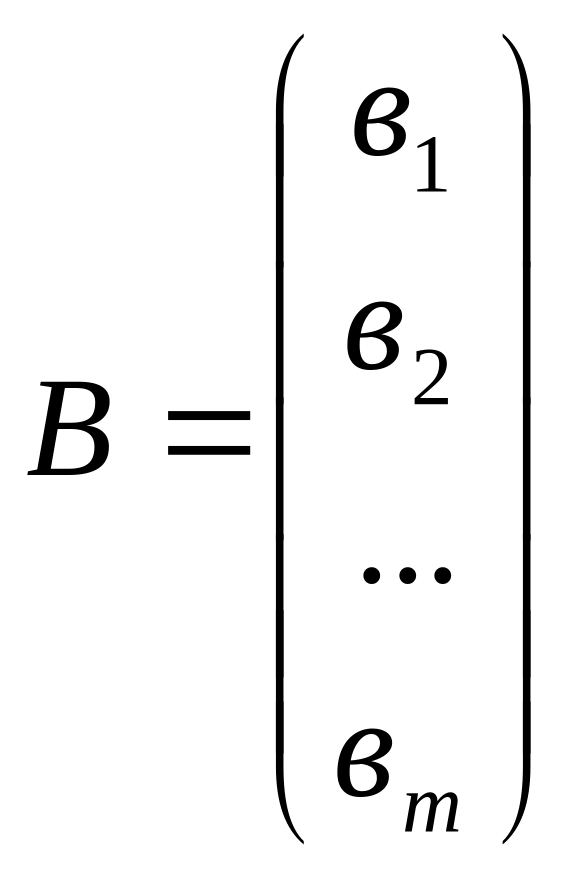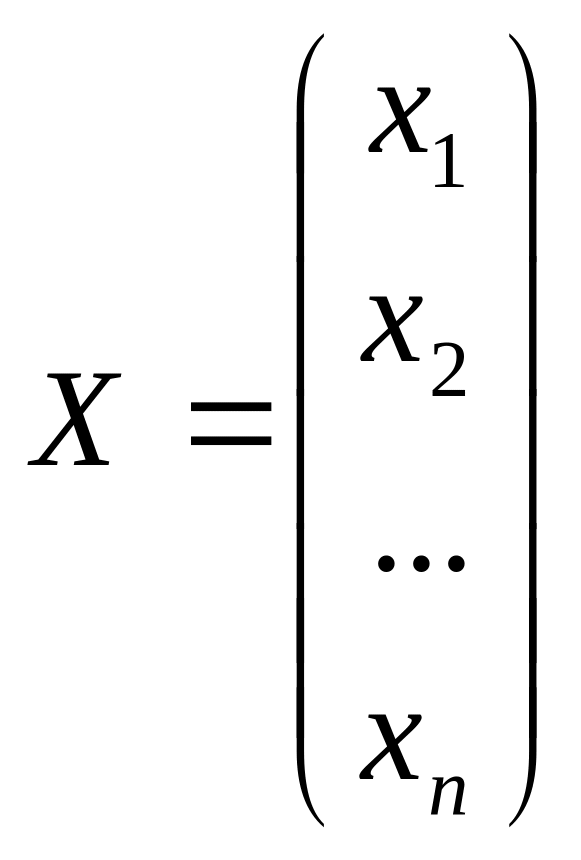Тогда с учетом правила произведения
матриц, исходная СЛАУ может быть записана
в матричном виде -
.
Такая запись позволяет использовать
при исследовании систем уравнений
матричную алгебру.
Решить систему – значит исследовать, совместна она или нет, и в случае совместности найти все решения системы. Здесь возможны два варианта – либо решение единственное, либо решений бесконечное множество.
2.2. Матричный метод решения невырожденных систем
.
Если в системе
, т.е. число неизвестных и число уравнений
совпадает, и определитель матрицы
системы
не равен нулю( система невырожденная!),
то для матрицы А существует обратная
.
Умножаем равенство
слева на
и учитывая, что
и
,
получим решение системы в матричной
форме:
.
Вывод: если квадратная
система уравнений невырожденная, то
она имеет единственное решение, которое
в матричной форме записывается в виде
.
Пример 2. Решить систему уравнений матричным методом.
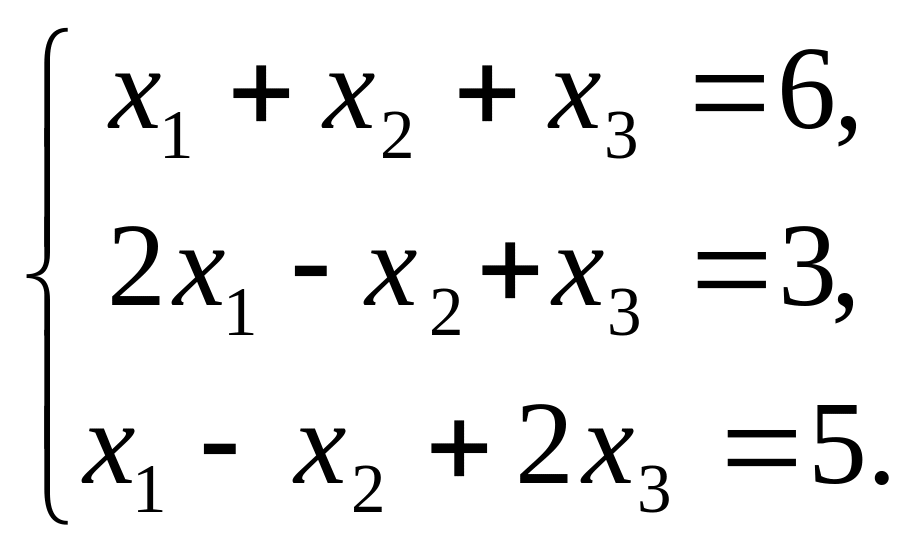
Решение. Определитель матрицы системы |A| = -5 ≠0 (проверьте!), значит, система совместна и имеет единственное решение. Найдем это решение. Для этого вычисляем обратную матрицу системы – А-1. Выпишем алгебраические дополнения к каждому элементу матрицы А.
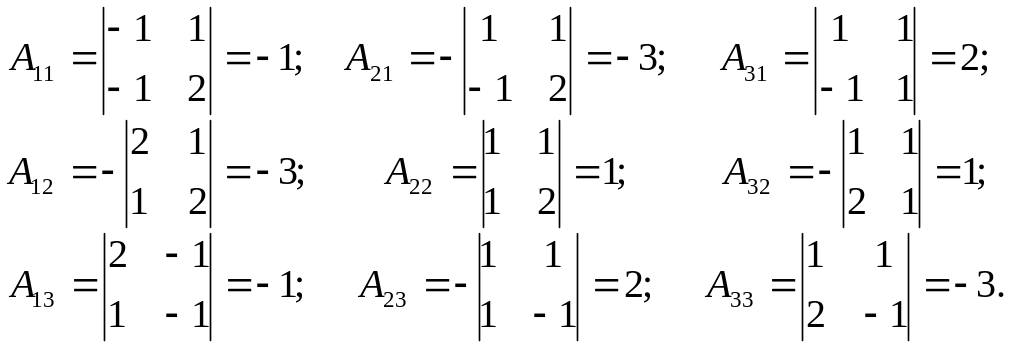
Обратная матрица имеет вид:
.
Тогда,
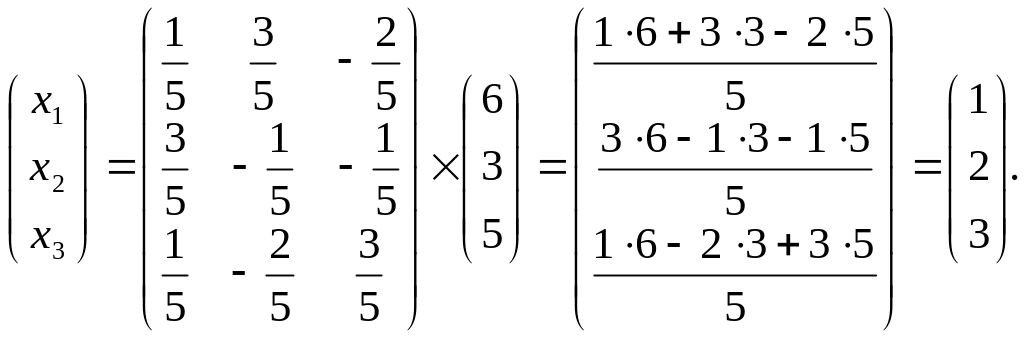
Ответ:
