5.2. Основные правила вычисления производных.

1. Если - константа, то , производная константы равна нулю.

2. Если , то , т.е. производная суммы равна сумме производных.

3. Если , то , производная произведения.

4. Если , где - константа, , т.е. константа выносится за знак производной.

5. Если , то , производная частного.

6. Если , то .

7. Если , где в свою очередь , то

- правило дифференцирования сложной функции, является очень важным при вычислении производных.

Замечание. Естественно, что во всех вышеприведенных формулах мы заранее постулируем существование указанных производных.

5.3 Таблица производных основных элементарных функций

Если функция, имеющая производную в точке х, и штрих – обозначает производную по переменной х, то верны следующие формулы.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

5.4. Примеры вычисления производных.

1.

2. .

3. .

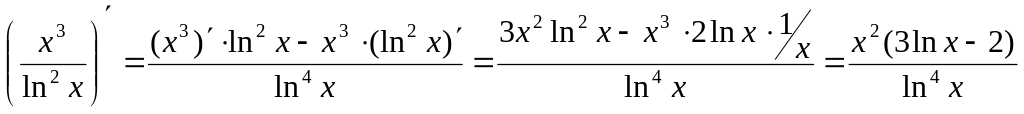4.

.

5.

=

.

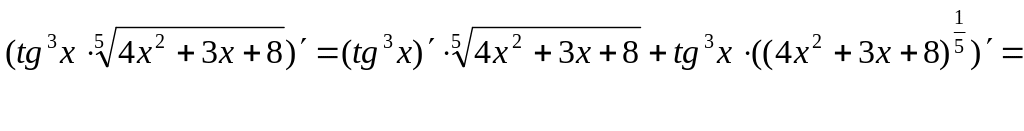
5.5. Дифференциал функции

Рассмотрим круг радиуса , площадь которого , то есть является функцией х. . Дадим положительное приращение , тогда, площадь круга радиуса равна . Приращение функции , геометрически представляет площадь соответствующего кольца . Легко видеть, что после несложных преобразований можно представить в виде . Так как , то. при величина - является бесконечно малой функцией более высокого порядка малости по сравнению с и обозначается , читается : « малое от ». Таким образом, приращение функции , представляется в виде суммы линейной относительно части, которая обозначается и называется дифференциалом функции и бесконечно малой функции более высокого порядка малости, чем .

В общем случае подобные рассуждения приводят к следующему определению дифференциала функции.

Определение. Если приращение функции в произвольной точке можно представить в виде , где от не зависит, то главная линейная часть приращения , называется дифференциалом функции в точке и обозначается , т.е. .

Сразу отметим, что поскольку разность между и есть бесконечно малая функция при , то при достаточно малом , можно приближенно полагать . Это приближенное равенство часто используется, как в приближенных вычислениях, так и при построении математических моделей различных процессов.

5.6. Связь производной и дифференциала.

Пусть функция имеет дифференциал, это значит, что приращение функции можно представить в виде . Разделим обе части этого равенства на . , и перейдем и пределу при . Очевидный результат этого предельного перехода существование производной и значит . Легко видеть, что верно и обратное утверждение. Таким образом, для того чтобы функция имела дифференциал в точке , необходимо и достаточно, чтобы она имела в этой точке производную. Поэтому, если функция имеет в некоторой точке производную, то говорят, что функция дифференцируема в этой точке.

Применив, полученное равенство к функции , с учетом того, что , получим . Поэтому окончательная формула для вычисления дифференциала функции

.

Отсюда следует и такой фундаментальный факт, выражение (читается «дэ игрек по дэ икс») является не просто неделимым обозначением производной, а отношением двух дифференциалов

.

Отметим, что приближенное равенство , используется в приближенных вычислениях в виде формулы:

.

Если обозначим , то эту формулу можно переписать в виде:

.

Многие приближенные формулы выводятся в окрестности нуля, то есть при :

Для некоторых элементарных функций эта формула дает следующие приближенные формулы при малых значениях :

; ; .

Пример. Найти дифференциал функции .

Решение. .

Пример. Вычислить приближенно .

Решение. = .