3.9. Системы линейных неравенств

Любая прямая делит плоскость на две части, полуплоскости. Причем, если для координат любой точки одной полуплоскости выполняется неравенство , то для координат любой точки другой полуплоскости – неравенство . Равенство нулю выполняется для координат точек самой прямой и только для них.

Чтобы определить в какой полуплоскости выполняется неравенство «больше», а в какой «меньше» нуля, достаточно подставить координаты любой точки. Чаще всего это точка . Если, например, подстановка нулевых значений даст С>0, то подстановка координат любой точки, лежащей в той же полуплоскости, что и т. , также даст положительное значение выражения .

Очевидно, что множество точек, координаты которых удовлетворяют системе линейных неравенств (решение системы неравенств), есть пересечение (общая часть) полуплоскостей, определяемых каждым из неравенств.

Пример. Изобразить на плоскости множество точек, определяемых системой неравенств

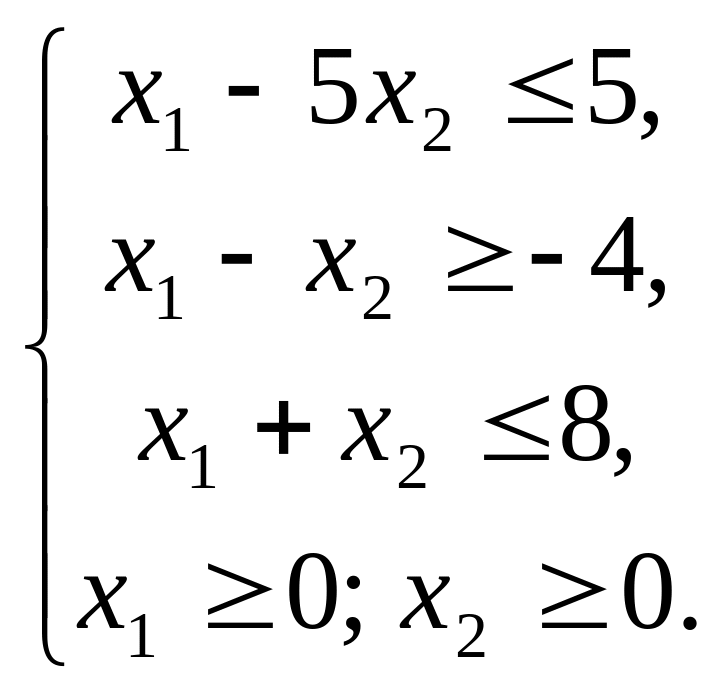
Решение. Рисуем на плоскости три прямые, задаваемые соответствующими равенствами. Для этого запишем каждое из уравнений

как уравнение прямой в отрезках, достаточно разделить каждое из уравнений на число, стоящее в правой части равенства:

Из уравнений видно, что первая прямая пересекает оси координат соответственно в точках с координатами (5; 0) и (0; -1); вторая прямая в точках (-4; 0) и (0; 4); третья – в точках (8; 0) и (0; 8). Подставляя в каждое из исходных неравенств начало координат – (0; 0), видим, что все три неравенства определяют полуплоскости содержащие начало координат. Решение системы, т.е. множество точек лежащих в первой четверти, координаты которых удовлетворяют всем трем неравенствам, изображено на рисунке.

4. Пределы

4.1. Множества, операции над множествами

Под множеством будем понимать совокупность неких объектов, объединенных по какому-либо признаку. Эти объекты - элементы множества. Множества обозначают, обычно, заглавными буквами латинского алфавита: , а элементы множеств соответствующими строчными . Факт принадлежности элемента данному множеству записывается так .

Если каждый элемент множества является в свою очередь элементом множества , то множество называется подмножеством множества , и записывают: .

Множества, имеющие конечное число элементов называются конечными множествами, в противном случае – бесконечными.

Множество не содержащее ни одного элемента называется пустым множеством: .

Множества задают либо перечислением элементов, либо описанием свойств множества, которые однозначно определяют принадлежность к данному множеству того или иного элемента. Элементы множества обычно записывают в фигурных скобках, например, А= {1,2,3,4,5} или В= {x : x²-1=0}- множество корней уравнения х²-1=0. После двоеточия идет описание свойства, которое определяет принадлежность данному множеству.

Множества можно определять также при помощи операций над некоторыми другими множествами. Пусть имеются два множества А и В.

Объединением (суммой) множеств и назовем множество , которое состоит из всех элементов, принадлежащих хотя бы одному из множеств или .

Например, если А={1,2,3,4,5) , В={1,3,5,7}, то .

Пересечением (произведением) множеств и назовем множество , которое состоит из всех элементов принадлежащих и множеству и множеству .

Например, . Множества ,не имеющие общих элементов ( ), называются непересекающимися.

Разностью двух множеств и называется множество , которое состоит из всех элементов принадлежащих , но не принадлежащих .

Например, А\В={2,4}.

Если , то разность называется дополнением множества до множества . Так, множество чисел Z\N ={ 0,-1,-2,-3,…,-n,…} является дополнением множества натуральных чисел N до множества целых чисел Z.