2.3. Правило Крамера для решения невырожденных систем
В п.1.1. мы вывели правило Крамера для решения СЛАУ второго порядка. Несложными выкладками можно показать, что аналогичные формулы верны для любых невырожденных квадратных систем, т.е. верно:
Правило Крамера: Если квадратная система n уравнений с n неизвестными невырожденная, то система имеет единственное решение, которое находится по формулам :
,
- главный определитель системы,
- определитель, полученный из
заменой
-го
столбца на столбец свободных членов.
Пример. Решить систему уравнений, применив правило Крамера:
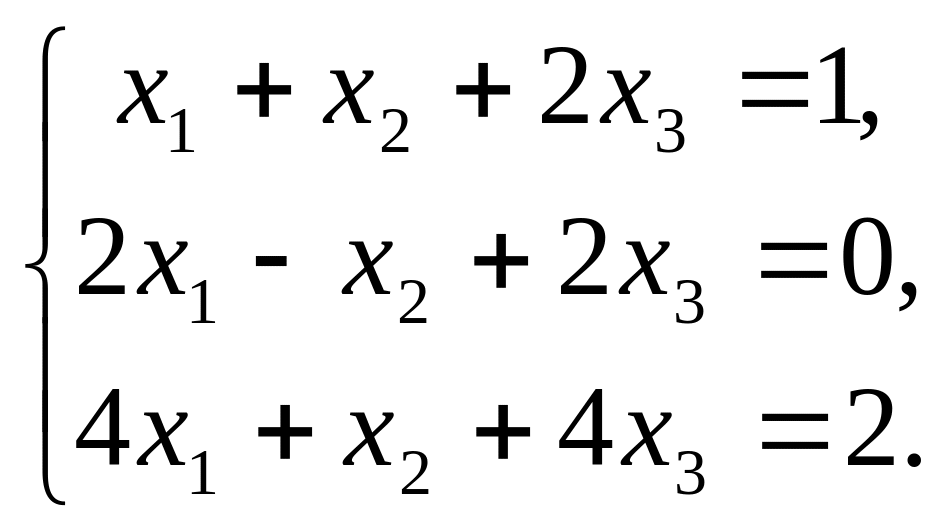
Решение. Найдем
главный определитель системы ∆ и
вспомогательные
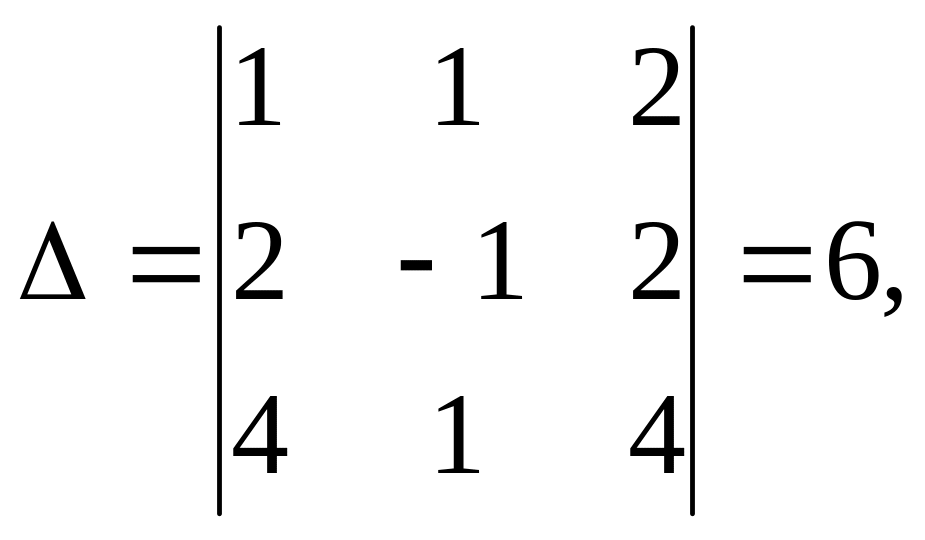
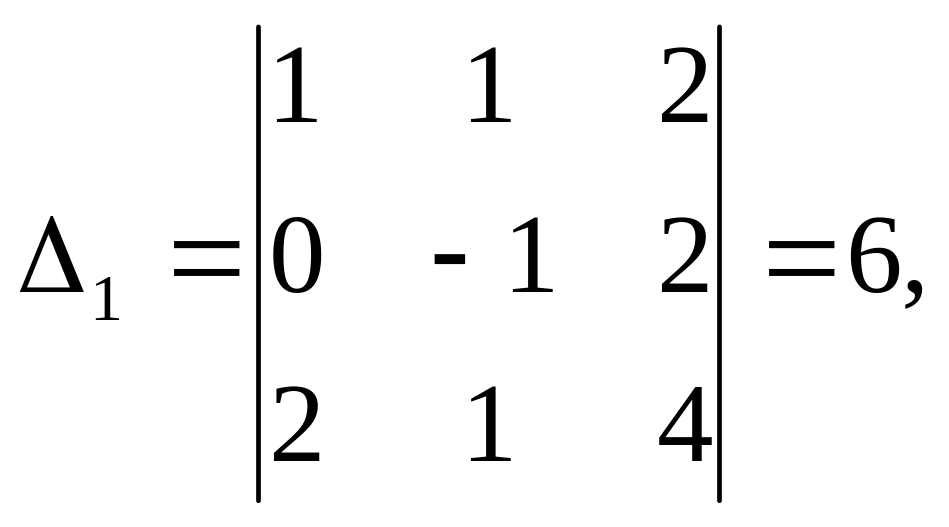
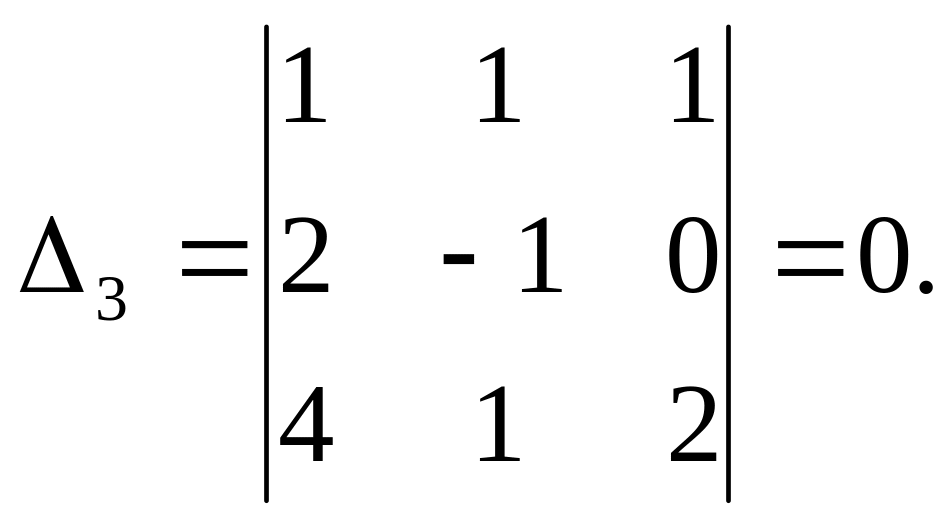
По правилу Крамера,
решение системы:
2.4. Решение произвольных систем
В случаях, когда число уравнений и число
неизвестных системы не совпадает,
,
или определитель квадратной системы
равен нулю, т.е. система вырожденная,
приведенные методы решения не подходят.
В этом случае, как правило, для решения
систем линейных уравнений применяют
метод исключения неизвестных, известный
также как метод Гаусса. Метод
основан на понятии эквивалентных
(равносильных) систем и элементарных
преобразований системы.
Определение. Две системы уравнений называются эквивалентными (равносильными), если они имеют одно и тоже множество решений.
Определение. Элементарными преобразованиями системы назовем:
1) умножение обеих частей любого уравнения системы на произвольный множитель отличный от нуля;
2) прибавление к любому уравнению системы другого уравнения этой же системы, умноженного на константу (положительную, отрицательную или равную нулю).
Легко показать,
что элементарные преобразования системы
приводят исходную систему к эквивалентной!
Суть метода Гаусса
– исключая последовательно, с помощью
элементарных преобразований системы,
неизвестные, привести
исходную систему к эквивалентной,
решение которой легко найти непосредственно.
Решение полученной системы уравнений
одновременно является решением исходной
системы. На практике процесс исключения
неизвестных разбивается на ряд этапов.
Сначала исключаем неизвестное
из всех уравнений, кроме первого. Для
этого к i-му (i
=2,…,m) уравнению системы
прибавим первое, умноженное на
.
В полученной системе, аналогично
исключаем неизвестное
из всех уравнений начиная с третьего,
затем
,
начиная с четвертого и так далее. В итоге
придем к одному из двух случаев:
1) в преобразованной системе (эквивалентной исходной!!!) появляется противоречивое уравнение 0 = в, где в ≠ 0. То есть система несовместна.
2) противоречивые уравнения в системе отсутствуют, и система принимает вид:
где коэффициенты
отличны
от нуля. Число, полученных в результате
элементарных преобразований, уравнений
системы r ≤ m
– числа уравнений в
исходной системе. Дело в том, что в
процессе преобразований очевидные
(тривиальные) уравнения, вида 0
= 0 , отбрасываются.
Переход от исходной системы к эквивалентной
называется прямым ходом
метода Гаусса.
Так как
система линейных уравнений полностью
определяется своей расширенной
матрицей (к матрице
системы добавляется столбец свободных
членов), то описанные выше преобразования,
проще выполнять не над уравнениями
системы, а над строками ее расширенной
матрицей. Отметим, также, что ранг матрицы
не изменяется при элементарных
преобразованиях ее строк. Это означает,
что в первом случае
ранг матрицы системы А
меньше ранга расширенной матрицы
системы
, и система несовместна.
Во втором случае, ранги этих матриц
совпадают и равны r
, т.е.
и система уравнений
совместна. И вообще,
верна важнейшая теорема теории СЛАУ -
Теорема Кронекера-Капелли. Для того чтобы система линейных алгебраических уравнений была совместна необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы системы
При решении совместных систем снова возможны два случая.
1) r
= n , система имеет
треугольный вид
и, тогда, начиная с последнего уравнения,
последовательно находится единственное
решение системы:
.
Указанный метод нахождения неизвестных, называется обратным ходом метода Гаусса.
2) r
< n, система имеет
трапециевидную форму.
В этом случае, число неизвестных больше
числа уравнений, поэтому первые r
неизвестных объявляем базисными,
а остальные n-r
неизвестных – свободными
. Придавая свободным неизвестным
произвольные значения
,
переносим их в правую часть уравнений
системы
и ,применяя обратный ход метода Гаусса,
выражаем базисные
неизвестные через
свободные.
Так как свободные неизвестные могут
принимать произвольные числовые
значения, делаем вывод , что исходная
система имеет бесчисленное множество
решений
.
Пример 1.
Решить систему уравнений
Решение. Легко увидеть, что определитель матрицы системы равен нулю, т.е. система вырожденная и, значит, изложенные ранее методы решения не подходят. Решим систему методом Гаусса. Будем проводить элементарные преобразования расширенной матрицы системы (прямой ход метода Гаусса):
.
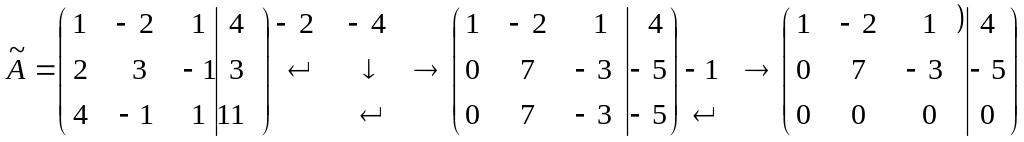Имеем,
меньше числа неизвестных n
= 3, значит,
базисные неизвестные,
R – свободное.
Полученной матрице соответствует
система двух уравнений
,
которая, после введения свободного
неизвестного
и переноса всех членов уравнений,
содержащих свободное неизвестное в
правую часть, примет треугольный вид:
Обратный ход метода Гаусса дает:
Таким образом, бесчисленное множество
решений системы можно записать в виде
{
где с
R.}.
Например, при с = 0 получим частное
решение (
.
Непосредственной подстановкой этого
решения в каждое из исходных уравнений
системы, можно убедиться в правильности
этого результата.