4.2. Предел функции

Одним из важнейших понятий математического анализа является понятие предельного перехода. С одной стороны, в некоторых случаях бывает достаточно очевидно, куда стремится значение функции , если аргумент стремится к какому-либо фиксированному значению (или - бесконечности). Например, стремится к , если , или , если .

Записывают этот факт так: , .

Но в большинстве случаев, результат такого предельного перехода не так очевиден, и для получения результата приходится использовать целый ряд теорем и свойств пределов, которые доказываются в курсе высшей математики. Их доказательство, прежде всего, основано на определении предела.

Определение. Число называется пределом функции при , если для любого, сколь угодно малого, существует , такое, что из неравенства следует, что .

Если решить указанные неравенства, то получим и , то есть можно сказать, что как только значение аргумента попадает в -окрестность точки , то соответствующее значение функции не выходят из -окрестности точки . Кратко, факт существования предела записывают так

.

Замечание 1. Аналогично можно дать понятие предела функции при и понятия односторонних пределов. В этом случае различают правосторонний предел, когда стремится к а, оставаясь все время больше и левосторонний предел, когда остается меньше .

Замечание 2. Огромную роль в анализе играет класс бесконечно малых функций при стремящихся к a. Функция называется бесконечно малой функцией (б.м.ф.) при , если . Бесконечно малые функции обычно обозначают греческими буквами: , , и т.п.

В противоположность б.м.ф., бесконечно большой функцией при называется функция , если .

4.3. Основные теоремы о пределах

Если существует , , то существуют и пределы суммы, произведения и частного этих функций, причем они равны сумме, произведении и частному пределов каждой из функций:

1) ;

2) ;

3) .

Следствия:

1) , предел константы равен этой константе;

2) , константа выносится за знак предела.

4.4. Непрерывность функции и вычисление простейших пределов

Каждый из нас имеет свое интуитивное представление о непрерывности. Как правило, мы считаем непрерывной ту функцию, график которой не имеет разрывов, т.е. представляет собой непрерывную линию. Этот факт в математике имеет строгое определение. Более того, мы дадим три эквивалентных определения непрерывности.

Определение1. Функция y=f(x) называется непрерывной в точке а, если она определена в некоторой окрестности этой точки и

Определение 2. Функция y=f(x) непрерывна в т. a , если бесконечно малому приращению аргумента в т.a соответствует бесконечно малое приращение функции, т.е. , где приращение функции в т. .

Определение 3. . Функция непрерывна в т.a _, если она определена в окрестности этой точки , предел слева в этой точке, равен пределу справа и равен значению. функции в этой точке : .

Функция непрерывная в каждой токе некоторого промежутка называется непрерывной на этом промежутке.

Естественно, точки в которых нарушаются условия непрерывности называются точками разрыва. Разрыв может быть конечным (первого рода), если односторонние пределы существуют, конечны, но не равны между собой, либо равны между собой, но не равны значению функции в рассматриваемой точке. Бесконечным (второго рода), когда хотя бы один из односторонних пределов бесконечен.

Можно показать, что все элементарные функции (функции, изучаемые еще в средней школе) непрерывны в каждой точке своего определения. Это позволяет, используя определения непрерывности и основные теоремы о пределах, вычислять простейшие пределы.

Пример 1. .

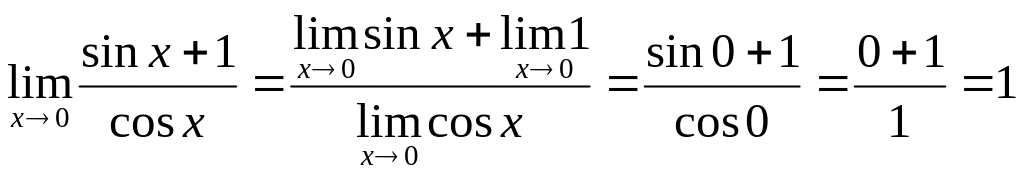При решении воспользовались непрерывностью функций в точке .

Пример 2. .

Здесь, воспользовались непрерывностью функций и .