6.4 Полное исследование функции и построение её графика.

Для построения графика функции нужно знать её свойства. Это, прежде всего, область определения функции, непрерывность, поведение функции вблизи границ области определения и точек разрыва, вертикальные асимптоты. Если функция периодична, то исследовать функцию достаточно в пределах одного периода. Графики четных функций симметричны относительно оси у, нечетных – относительно начала координат, это позволяет исследовать поведение функции только при . Если это не вызывает больших вычислительных трудностей, определяются точки пересечения с осями координат и участки знакопостоянства функции. По этим данным рисуется график функции в первом приближении.

Для уточнения графика функции вычисляем первую производную и исследуем функцию на монотонность и экстремумы. Далее, находим вторую производную, участки выпуклости и вогнутости, точки перегиба. В заключение, ищем наклонные асимптоты и рисуем окончательный график функции.

Отметим, что порядок действий при исследовании функций не догма и может быть изменен исследователем. Более того, при необходимости можно получить дополнительный ряд значений функции при некоторых частных значений аргумента.

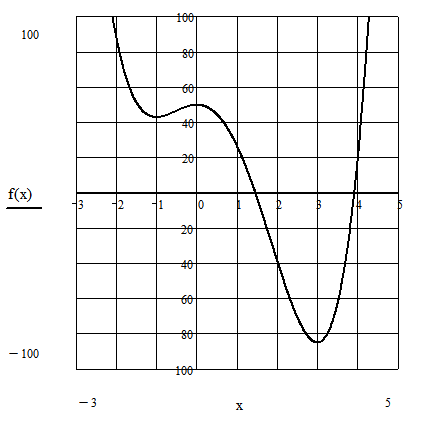
Ниже, на рисунке приведен схематический график функции , исследование которой мы, практически, полностью провели в предыдущих разделах. Отметим только очевидные свойства функции - непериодична, не является ни четной, ни нечетной и при значения функции

6.5. Наименьшее и наибольшее значения функции

Рассматривая непрерывные функции, мы отмечали такой важное свойство: функция непрерывная на замкнутом отрезке [a;b] достигает на этом отрезке своего наибольшего и наименьшего значения, причем эти значения могут приниматься либо в критических точках внутри отрезка, либо на его границе. Таким образом, задача нахождения этих экстремальных значений достаточно проста и разбивается на несколько этапов.

Этап 1. Находим критические точки первой производной и выбираем из них те, которые лежат в рассматриваемом интервале (a;b).

Этап 2. Вычисляем значения функции в найденных критических точках и на концах интервала в точках a и b.

Этап 3. Выбираем из полученных значений наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2;1].

Решение. Находим первую производную и приравниваем к нулю, . Решаем полученное уравнение: , получим стационарные (критические) точки , которые обе лежат в заданном промежутке.

Вычисляем значения функции в критических точках и в граничных точках отрезка: . Простой визуальный анализ полученных значений показывает, что .

6.6 Экономическая интерпретация первой производной (предельный анализ)

В экономических приложениях первая производная обычно понимается как предельная или маржинальная функция. Поскольку , то приближенно описывает изменение функции при изменении независимой переменной на одну единицу, т.е. при значение производной равно изменению функции .

В отличие от средних величин, широко используемых в экономике - средняя стоимость продукции, средняя производительность труда, средний доход, средний объем продаж и т.д., дифференциальное исчисление позволяет ответить на вопрос: на какую величину вырастет результат, если будут увеличены затраты, или, наоборот, насколько уменьшится результат, если затраты сократятся, т.е. изучить процесс в динамике. В подобных задачах находят предел отношения приращений рассматриваемых величин или, как говорят, предельный эффект.

Пример 1. Пусть функция выражает зависимость суммарного дохода R от количества товара Q, тогда производная - выражает, по определению, предельный доход. Он приближенно равен изменению суммарного дохода при изменении количества реализованного товара на единицу т.е. показывает насколько вырастет суммарный доход, если количество реализованного товара увеличится на единицу.

Пример 2. Если C= f(Q) – функциональная зависимость издержек (затрат) С от объема продукции Q, то - это предельные издержки, т.е. показывает изменение полных издержек при изменении выпуска продукции на единицу.

Пример 3. Пусть Q=f(L)- производственная. Функция, выражает зависимость количества выпускаемой продукции Q от приложенного труда L ( численности персонала) , тогда - предельная производительность труда, показывает приближенно, насколько изменится (увеличится или уменьшится) объем выпускаемой продукции при изменении численности персонала на единицу.

Рассмотрим производственную функцию , можно считать, что это эмпирическая зависимость. Предельная производительность труда в этом случае дается формулой Проанализируем зависимость предельной производительности труда от численности персонала. Для этого произведем некоторые расчеты, которые сведем в следующую таблицу.

L	1	25	100	2500
	146	26	11	-1

Из таблицы видно, что предельная производительность труда падает с ростом численности персонала, причем, начиная с некоторого значения, она становится отрицательной. Это означает, что при дальнейшем росте численности персонала будет падать не только предельная производительность, но и производство продукции

Отметим, что рассмотренные предельные величины характеризуют абсолютные изменения функции в отличие от эластичности, описывающей относительные изменения функции как реакцию на относительные изменения аргумента.