Раздел 4. Статистика равновесных носителей заряда

4.1 Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.

4.2 Концентрация электронов и дырок в зонах для различных степеней вырождения электронного или дырочного газа.

4.3 Статистика примесных состояний. Функция распределения электронов и дырок по примесным состояниям. Плотность примесных состояний. Примесные зоны. Влияние температуры и концентрации примеси на концентрацию свободных электронов и дырок.

4.4 Плотность квантовых состояний в квантово-размерных структурах с квантовыми ямами, квантовыми нитями и квантовыми точками.

4.1 Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.

Для определения  твердого тела необходимо знать равновесную (темновую) концентрацию электронов (n) и дырок (p).

Для определения n и p необходимо знать параметры зон – плотность квантовых состояний и вероятность их дополнения – функцию распределения электронов и h⁺ по состояниям.

Функции распределения электронов и дырок по квантовым состояниям разрешения зон (зона проводимости и валентная зона).

Электроны в металлах, полупроводниках подчиняются квантовой статистике. Вероятность заполнения уровня E при температуре T определяется функцией Ферми – Дирака:

Электроны проводимости – фермионы – частицы, обладающие полуцелым спином, и подчиняются принципом Паули:

F – уровень (энергия) Ферми, или электрохимический потенциал.

Основные свойства функции f_Ф-Д :

При T  0

При T = 0 функция терпит разрыв (то есть функция не определена).

Из графика следует, что f есть уровень, который разделяет занятые электронами состояния в зоне проводимости от свободных.

В металлах при T = 0: уровень F соответствует максимальной энергии электронов в зоне проводимости – энергии Ферми.

В - пространстве вводят

поверхность Ферми,

которая соответствует энергии E_F.

Внутри сферы Ф – находятся электроны проводимости.

Проводимость по зоне проводимости - есть жесткое смещение сферы Ф в - пространстве под действием внешнего электрического поля на величину k_x.

При температурах T  0:

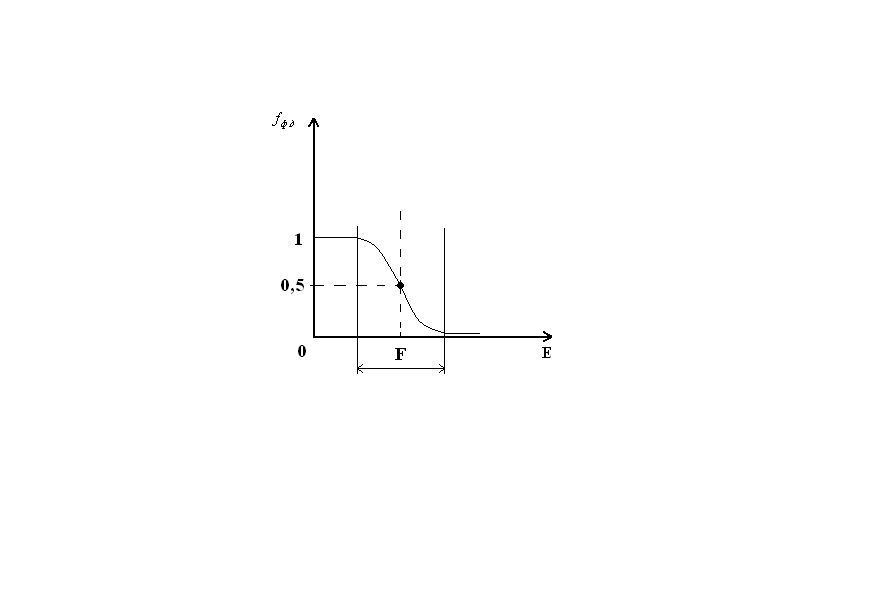
f_Ф-Д = 0,5 и F имеет смысл уровня, вероятность заполнения которого ½.

Функция f_Ф-Д претерпевает наибольшее изменение для энергий вблизи F.

При (E – F)  kT функция f_Ф-Д переходит в классическую функцию Максвелла – Больцмана:

– это высокоэнергетический хвост функции f_Ф-Д.

Уровень F ниже Ec на энергию не меньше kT.

В этом случае действует классическая статистика Максвелла – Больцмана и полупроводников, подчиняющиеся этой статистике – невырожденные (по концентрации).

Невырожденный полупроводник n-типа – полупроводник, в котором уровень F лежит ниже Ec в запрещенной зоне на величину не меньше kT.

Таким образом, в невырожденном полупроводнике на уровне f – нет электронов в отличие от металла!

Невырожденный полупроводник p-типа – уровень F лежит выше Ec на величину kT.