Пример 1. Обработка результата однократного измерения

На вольтметре класса точности 2,5 с пределом измерений 300 В зарегистрировано значение измеряемого напряжения х = 267,5 В.

При _кл = 2,5% и Х_k = 300 В абсолютная погрешность равна:

= 7,5 (В)  8 (В) .

Относительная погрешность в этом случае равна:

В соответствии с приведенными выше правилами, в окончательном ответе должно быть зафиксировано, что значение напряжения: ; измерение произведено с относительной погрешностью .

5. Обработка результатов прямых многократных наблюдений

Метод однократного измерения используется обычно только для минимальной по точности оценки измеряемой величины и в случаях, когда невозможно обеспечить реализации серии повторных однотипных наблюдений.

Для повышения точности измерений используется метод, основанный на статической обработке результатов многократных наблюдений. Статистика указывает на возможность уменьшения случайной составляющей погрешности за счет: 1) усреднения результатов серии наблюдений; 2) увеличения количества этих наблюдений.

Обозначим значения ряда последовательных наблюдений как х₁, х₂, … х_n. Эти значения являются лишь частью множества значений, которые могут появиться при измерении данной физической величины, т.е. они являются выборочными. Поэтому рекомендуется порядок обработки результатов прямых многократных наблюдений, изложенный в следующих пунктах.

1. Результаты наблюдений подвергаются анализу с целью поиска грубых погрешностей (промахов).

Наблюдения с обнаруженными промахами отбрасываются. Методика отбрасывания базируется на сопоставлении: (а) отклонения значения наблюдения от среднего арифметического значения ряда наблюдений; (б) среднеквадратического отклонения результата наблюдения.

Среднее арифметическое значение ряда наблюдений рассчитывается по формуле:

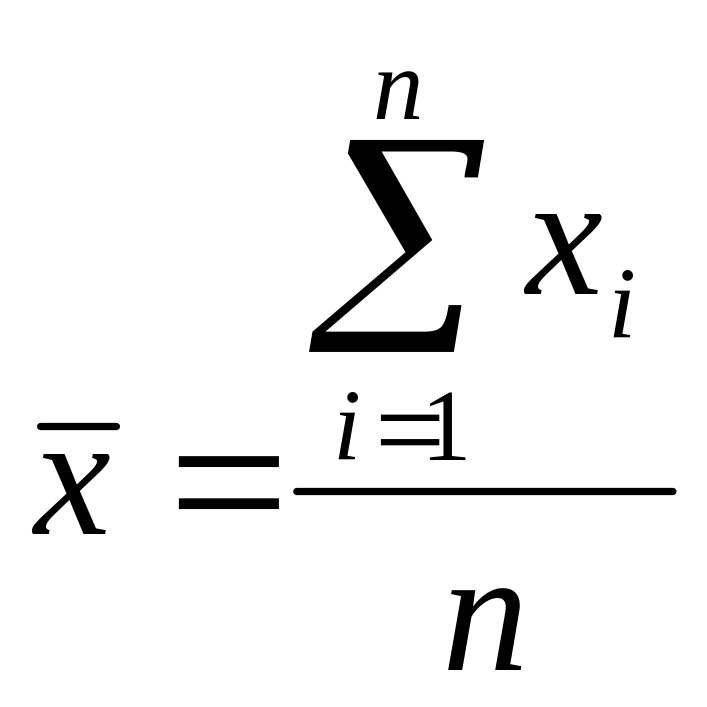, (1)

где: i- индекс значения наблюдения (i изменяется в пределах от 1 до n).

Среднеквадратическое отклонение наблюдения вычисляется по формуле:

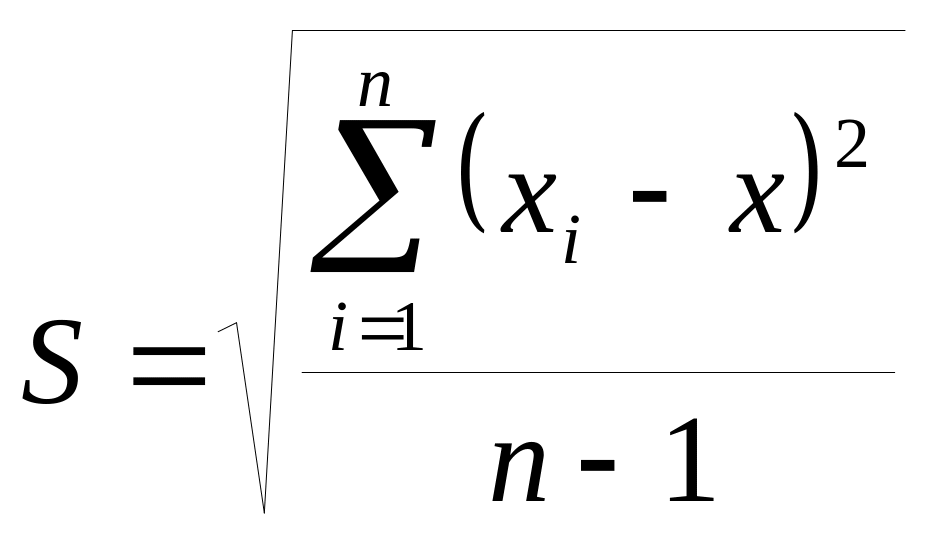. (2)

В случае ряда из n  6 наблюдений выявление промахов по отклонениям отдельных измерений от применять не следует.

Если n  6 , то результат наблюдения х_i является промахом, если:

В случае выявления промаха значения х и S вычисляются без использования соответствущего значения наблюдения.

2. На основании формулы (2) следует вычислить оценку среднеквадратического отклонения результата по формуле:

. (3)

Эта величина характеризует отклонение среднего значения серии наблюдений от действительного значения измеряемой величины х_о (при отсутствии систематической погрешности).

3. Вычисленное по формуле (3) среднее значение является случайной величиной и представляет собой точечную оценку истинного значения измеряемой величины х_о. Эту оценку необходимо дополнить доверительным интервалом . Значение доверительного интервала показывает, что с заданной вероятностью этот интервал включает в себя истинное значение измеряемой величины х_о. Вероятность того, что истинное значение измеряемой величины х_о попадает в заданный доверительный интервал , называется доверительной вероятностью . В соответствии с ГОСТ 8.207-76 [1] при проведении технических и научных измерений следует использовать значение , равное 0,95. В особых случаях, например, когда результаты имеют значение для здоровья людей, допускается вместо  = 0,95 принимать  = 0,99 и более высокие значения.

Далее следует определить значение коэффициента Стьюдента t_0,95 для конкретного количества наблюдений n (таблица 1). Затем следует вычислить абсолютную случайную погрешность х_сл (доверительную границу погрешности) при доверительной вероятности  по формуле:

Δ х _сл = t_{α, n} . (4)

Примечание. При прямых измерениях может оказаться, что для результатов отдельных отсчетов все . В этом случае доверительная граница погрешности прямых измерений определяется приборной погрешностью, которая имеет и систематическую, и случайную составляющие.

4. Абсолютная приборная погрешность вычисляется по одной из трех формул.

4.1. Если класс точности прибора указан одним числом _кл , то:

(5)

где Х_k – предел использованного диапазона измерений прибора;

4.2. Если класс точности прибора указан одним числом _кл, заключенным в кружок, то:

, (6)

где х – значение измеряемой величины.

Таблица 1