§ 5. Замечательные пределы

Первый замечательный предел

= 1,

неопределенность: .

○ Рассмотрим окружность радиуса 1:

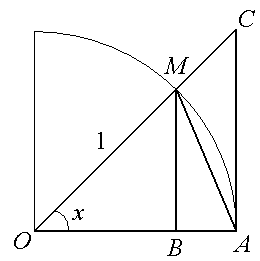
Обозначим центральный угол через , при этом пусть .

Из рисунка следует

(1)

,

,

.

Тогда выражение (1) примет вид:

< <

или

< < .

Разделим на :

1 < <

или

1 > > .

Последнее неравенство получено для , но

= и = .

Следовательно, последнее неравенство справедливо и для . Переходя к пределу, получим

= 1, = 1.

Следовательно, согласно теореме 2, имеем

= 1. ●

Пример. Найти предел

.

□ Имеем

= = = = ∙ = . ■

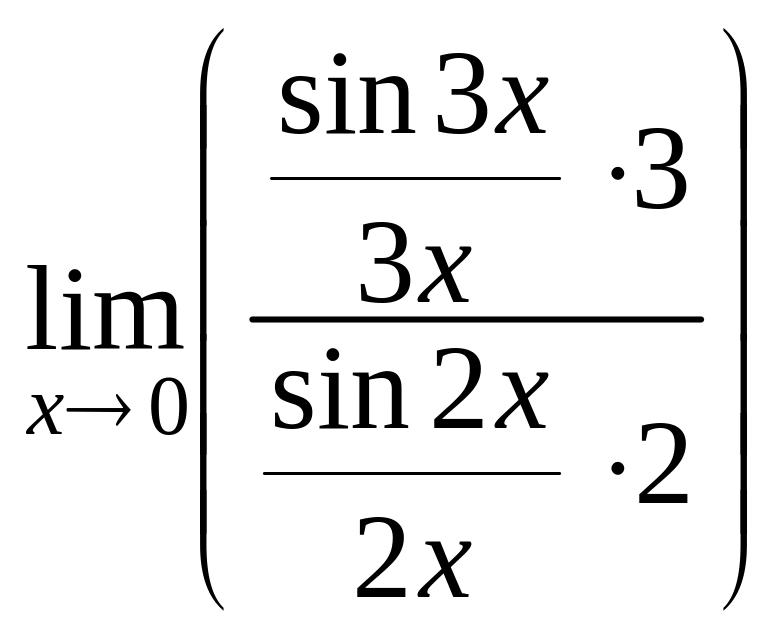Второй замечательный предел

,

неопределенность: ; = 2,7182… .

○ Известно, что . Пусть теперь , принимая как дробные, так и отрицательные значения.

1. Пусть . Каждое его значение заключено между двумя положительными числами: < . При этом будут выполняться неравенства:

≥ > , 1+ ≥ 1+ > 1 + ,

> > .

Если , то, очевидно, и . Тогда

= = =

= ;

= = = .

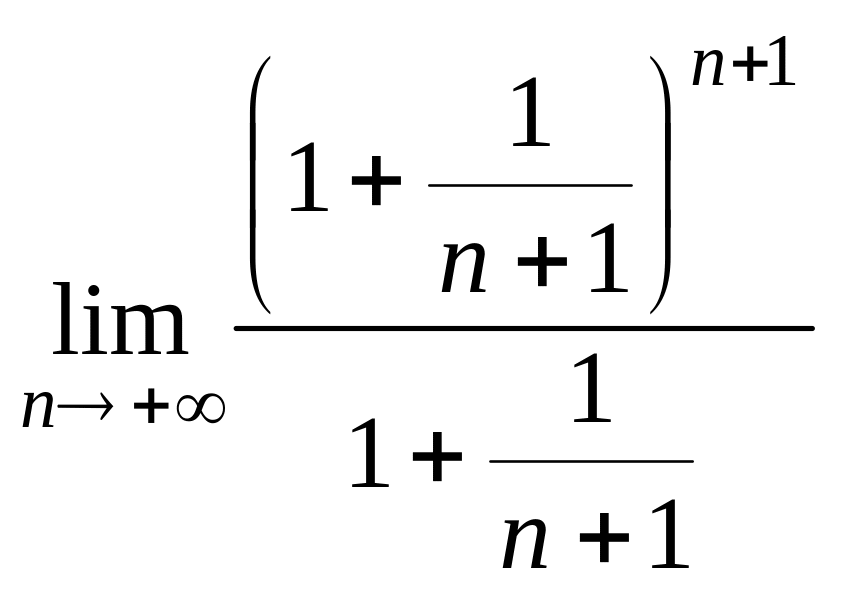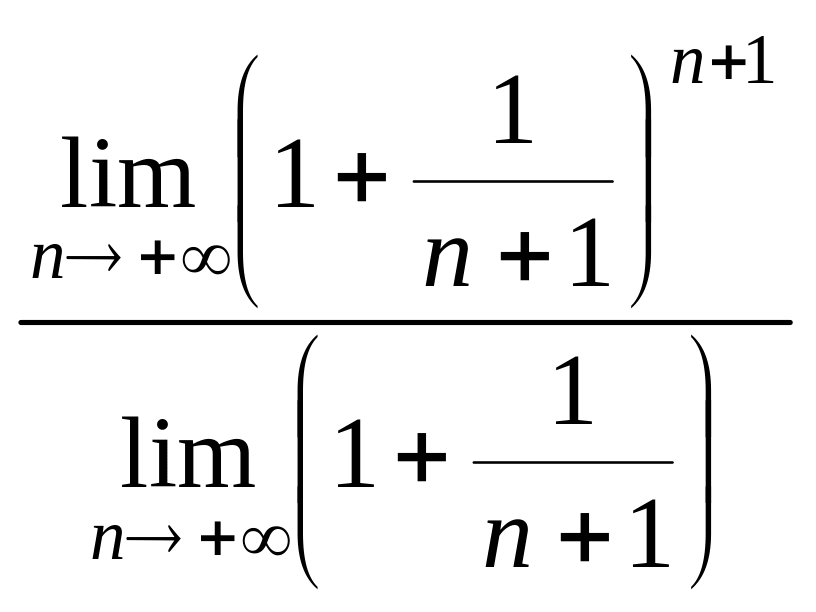Следовательно, согласно теореме 2, имеем

.

2. Пусть . Введем новую переменную или . При будет . Можем написать

= = = =

= = = .

Объединяя оба случая, получим

. ●

Замечание. Пусть = . Если , то и получаем

= = .

Другими словами, получили другую запись второго замечательного предела

= .

Пример. Найти предел

.

□ Рассмотрим общий метод применения второго замечательного предела для вычисления пределов:

= = = = =

= = = = = !

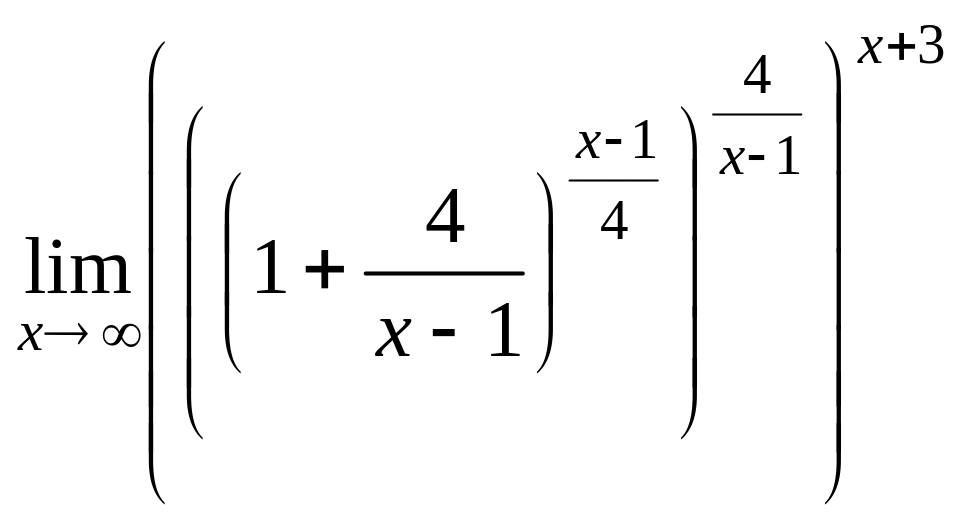= = 4

! = . ■

§ 6. Бесконечно малые и бесконечно большие функции

Функция f(x) называется бесконечно малой функцией (или просто бесконечно малой) в точке х = х₀ (или при х → х₀), если = 0.

На языке “ ε −δ ”:

Функция f(x) называется бесконечно малой в точке х = х₀, если для ε > 0 δ > 0 такое, что для х Х, х ≠ х₀, удовлетворяющих неравенству

| х − х₀| < δ,

выполняется неравенство

| f(x)| < ε.

Аналогично при х →х₀+, х →х₀−, х →+∞, х →−∞, х →∞.

Замечание 1. Равенство = А можно записать в виде

f(x) = А + (х),

где (х) − бесконечно малая при х→х₀.

Свойства бесконечно малых:

Алгебраическая сумма и произведение конечного числа бесконечно малых функций при х → х₀, и также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при х → х₀.

Аналогично при х →х₀+, х →х₀−, х →+∞, х →−∞, х →∞.

Функция f(x) называется бесконечно большой функцией (или просто бесконечно большой) в точке х = х₀ (или при х → х₀), если для ε > 0 δ > 0 такое, что для х Х, х ≠ х₀, удовлетворяющих неравенству

| х − х₀| < δ,

выполняется неравенство

| f(x)| > ε.

В этом случае пишут = ∞ и говорят, что функция стремится к бесконечности при х → х₀ или что она имеет бесконечный предел в точке х = х₀.

Если же выполняется неравенство f(x) > ε ( f(x) < −ε), то пишут = +∞ ( = −∞) и говорят, что имеет в точке х = х₀ бесконечный предел, равный +∞ (−∞).

По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:

= +∞, = −∞,

= +∞, = −∞.

Аналогично определяются бесконечно большие функции при х →+∞, х →−∞, х →∞.

Замечание 2. Между бесконечно малыми и бесконечно большими функциями существует такая же связь, как и между соответствующими последовательностями: функция, обратная бесконечно малой, является бесконечно большой, и наоборот.

Сравнение бесконечно малых и бесконечно больших функций

Пусть при х → х₀ функции (х) и (х) являются бесконечно малыми. Тогда:

1. если = 0, то (х) называется бесконечно малой более высокого порядка, чем (х): (х) = о( (х));

2. если = А ≠ 0 (А − число), то (х) и (х) называются бесконечно малыми одного порядка (имеют как бы “одинаковую скорость“ стремления к нулю);

3. если = 1, то (х) и (х) называются эквивалентными бесконечно малыми: (х) ~ (х);

4. если = А ≠ 0, то (х) называют бесконечно малой п-го порядка относительно (х).

Аналогично при х →х₀+, х →х₀−, х →+∞, х →−∞, х →∞.

Пример. Сравнить бесконечно малые (х) = х и (х) = 2х при х → 0.

□ Найдем предел

= = .

Следовательно, (х) и (х) являются бесконечно малыми одного порядка. ■

Замечание 1. При х → 0: ~ х, ~ kх, ~ х^k (аналогично для арксинуса, тангенса, арктангенса), ~х, ~ х , ~ х, − 1 = .

Пример. Найти предел

.

□ Имеем

= = | ~ 2x| = = 2. ■

Замечание 2. Если функции (х) и (х) есть бесконечно малые в точке х₀, то функция (х)∙ (х) имеет более высокий порядок малости, чем каждый из сомножителей, т.е.

(х)∙ (х)=о( (х)), (х)∙ (х)=о( (х)).

Для бесконечно больших функций имеют место аналогичные правила сравнения.