§ 3. Монотонные последовательности
Последовательность называется возрастающей, если
,
неубывающей, если
,
убывающей, если
,
невозрастающей, если
.
Все такие последовательности объединяются общим названием монотонные. Возрастающие и убывающие последовательности называются также строго монотонными.
Монотонные последовательности ограничены по крайней мере с одной стороны. Если монотонная последовательность ограничена с обеих сторон, т.е. является ограниченной, то она сходится. Другими словами, справедлива следующая теорема.
Теорема. Монотонная ограниченная последовательность имеет предел.
Число
Пусть
дана последовательность
с общим членом
=
:
,
,…,
,
…
Последовательность
монотонно возрастающая и ограничена
(2 <
<
3).
Следовательно, она имеет конечный
предел. Этот предел называют числом
е.
Таким образом,
= ( = 2,7182…).
Логарифм
с основанием
называют натуральным
логарифмом
и
обозначают
.
§ 4. Предел функции
Пусть функция
определена на некотором промежутке
(
может быть
,
,
и т.д.) и пусть точка
или
.
Возьмем из
последовательность точек, отличных от
… , , …, (1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно говорить о существовании ее предела.
Определение 1. “на языке последовательностей”
Число
называется пределом
функции
в точке
(или при
),
если для любой сходящейся к
последовательности (1) значений
аргумента
(
),
соответствующая последовательность
(2) значений функции сходится к числу
.
Запись:
.
Определение
2. “на языке
”
Число
называется пределом
функции
в точке
,
если для
такое, что для
,
,
удовлетворяющих неравенству
,
выполняется неравенство
.
Геометрический смысл.
Распишем модульные неравенства:
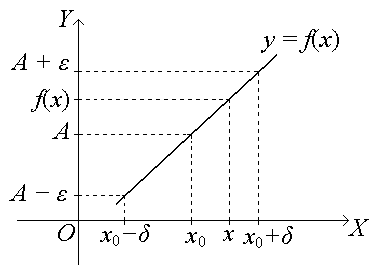
Как
только аргумент
попадает в
точки
,
то
попадает в
точки
и при приближении
к
значения функции
приближаются к числу
.
Пример.
Доказать, что
.
□ Возьмем
.
Задача сводится к тому, чтобы по этому
найти такое
,
при котором из неравенства
=
следовало бы неравенство
=
.
Имеем
,
или
.
Отсюда
видно, что если взять
,
то для всех
,
удовлетворяющих неравенству
,
выполняется требуемое неравенство
.
Это и означает, что
.
В
частности, если
,
то
;
если
,
то
;
если
,
то
и т.д. Таким образом,
зависит от
.
Поэтому в определении предела иногда
пишут
.
■
Если
стремится к пределу
при
,
стремящемся к
так, что
принимает только значения, меньшие
,
то пишут
(
)
и называют этот предел пределом функции в точке слева.
Если принимает только значения, большие , то пишут
(
)
и называют этот предел пределом функции в точке справа.
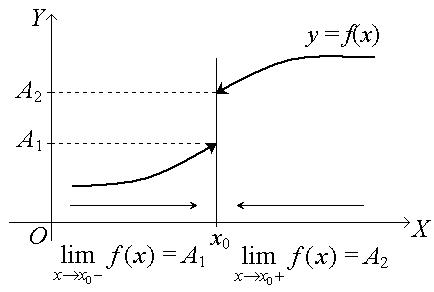
Если предел справа и предел слева существуют и равны, т.е. А1 = А2 = А, то А будет пределом в смысле данного определения предела в точке , т.е.
=
=
.
Число
А
называется пределом
функции
при
(
),
если для любой бесконечно большой
последовательности (1) значений
аргумента, элементы
которой положительные (отрицательные),
соответствующая последовательность
(2) значений функции сходится к числу
А.
Число
А
называется пределом
функции
при
,
если для любой бесконечно большой
последовательности (1) значений
аргумента, соответствующая последовательность
(2) значений функции сходится к числу
А.
Если пределы функции при и при равны А, то пишут
= А.
Пример.
□
Пусть дана функция
=
.
Так как
= 0 и
= 0, то можно записать
= 0. ■
Основные теоремы о пределах функции
Теорема
1.
Пусть функции
и
имеют в точке
пределы
и
.
Тогда функции
,
и
(при
≠
0) имеют в точке
пределы, равные соответственно
,
и
.
○ Пусть
(
)
– произвольная, сходящаяся к
последовательность значений аргумента
функций
и
.
Соответствующие последовательности
и
значений этих функций имеют пределы
и
.
Но тогда, в силу соответствующей теоремы
о пределах последовательностей,
последовательности
,
и
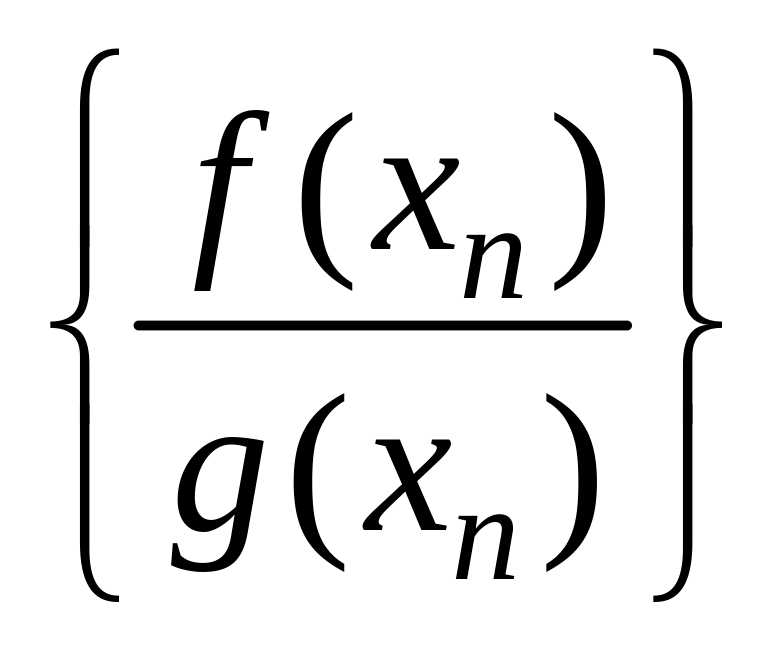(при
≠
0) имеют пределы, соответственно равные
,
и
.
Согласно определению 1 предела функции,
это означает, что
=
,
=
,
=
.
●
Следствие. Постоянный множитель можно выносить за знак предела, т.е.
=
.
Теорема
2.
Пусть функции
,
и
определены в некоторой окрестности
точки
,
за исключением, быть может, самой точки
,
и функции
,
имеют в точке
предел, равный А,
т.е.
=
= А.
Пусть,
кроме этого, выполняются неравенства
.
Тогда
= А.
○ Пусть
(
)
– произвольная, сходящаяся к
последовательность значений аргумента
функций
и
.
Соответствующие последовательности
и
значений этих функций имеют предел,
равный A,
т.е.
,
при
.
Используя неравенства, данные в условии,
можно записать
.
Отсюда,
согласно соответствующей теоремы о
пределах последовательностей, следует,
что
.
В силу определения 1 предела функции, это означает, что
= А. ●
Замечание.
Теоремы 1 и 2 верны при
,
,
,
,
.
Пример. Найти предел
.
□ Имеем
=
=
=
=
=
=
=
.
■
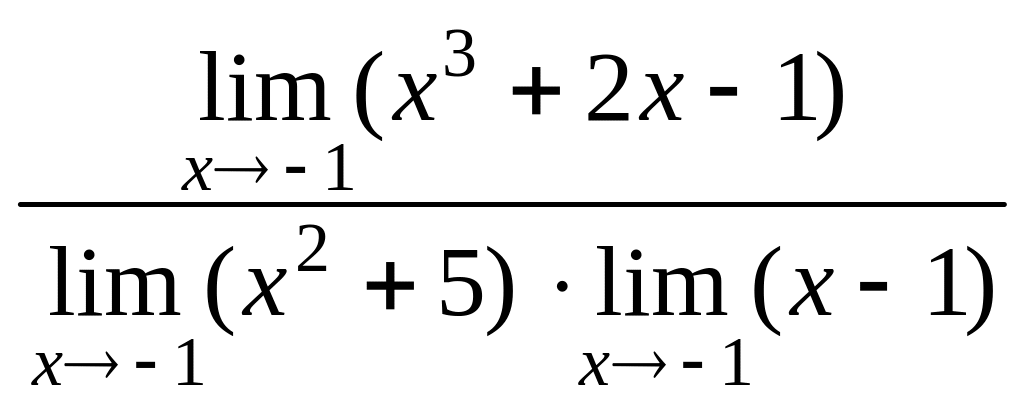