§ 13. Градиент

Пусть в области D задана функция u = u(х, у, z).

Вектор

(1)

называется градиентом функции u = u(х, у, z).

Говорят, что в области D определено векторное поле градиентов.

Часто говорят, что задан градиент скалярного поля u, т.к. функция u определяет скалярное поле.

Пусть единичный вектор соответствует :

= .

Тогда

(2)

или

, (3)

или

, (4)

или

. (5)

т.е. скорость изменения скалярного поля по некоторому направлению равна проекции градиента на это направление.

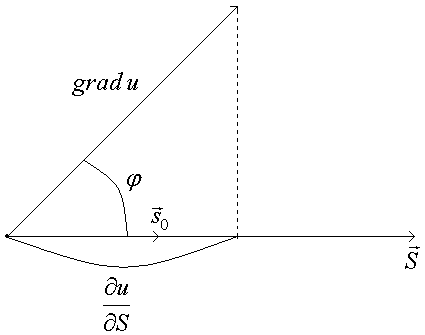
Замечание. Вектор перпендикулярен поверхности уровня

u(х, у, z) = С.

Свойства градиента:

1⁰. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента; это наибольшее значение производной равно .

Другими словами, наибольшая скорость изменения скалярного поля при совпадении направлений и .

Действительно, из (4) следует, что при : .

2⁰. Производная по направлению вектора , перпендикулярного к вектору , равна нулю.

Действительно, из (4) следует, что при : .

3⁰. .

4⁰. .

Пример. Дана функция u = х² + у² + z².

а) Найти градиент в точке М(1; 1; 1) .

□ Выражение градиента этой функции в произвольной точке будет иметь вид:

.

Следовательно,

.

Тогда, длина градиента равна:

.

Найти производную от функции u в точке М(1; 1; 1) в направлении градиента.

□

.

Направляющие косинусы:

; ; .

Следовательно,

,

т.е. . ■

Если дана функция u = u(x, y), то

и градиент лежит в плоскости ХОУ. Этот градиент перпендикулярен линии уровня:

§ 14. Касательная плоскость и нормаль к плоскости

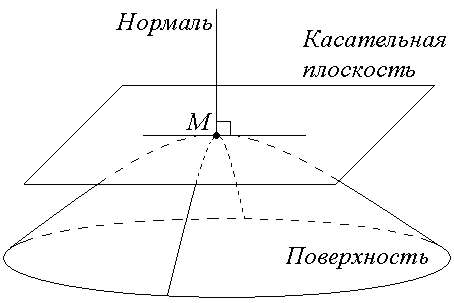
Если поверхность задана неявно, т.е. уравнением

F(x, y, z) = 0,

а касательная плоскость проходит через точку М(х₀, у₀, z₀), то уравнение этой плоскости имеет вид:

(1)

Если поверхность задана явно, т.е. уравнением

z = f(x, y),

то уравнение касательной плоскости имеет вид:

. (2)

Если поверхность задана неявно, т.е. уравнением

F(x, y, z) = 0,

то уравнение нормали имеет вид:

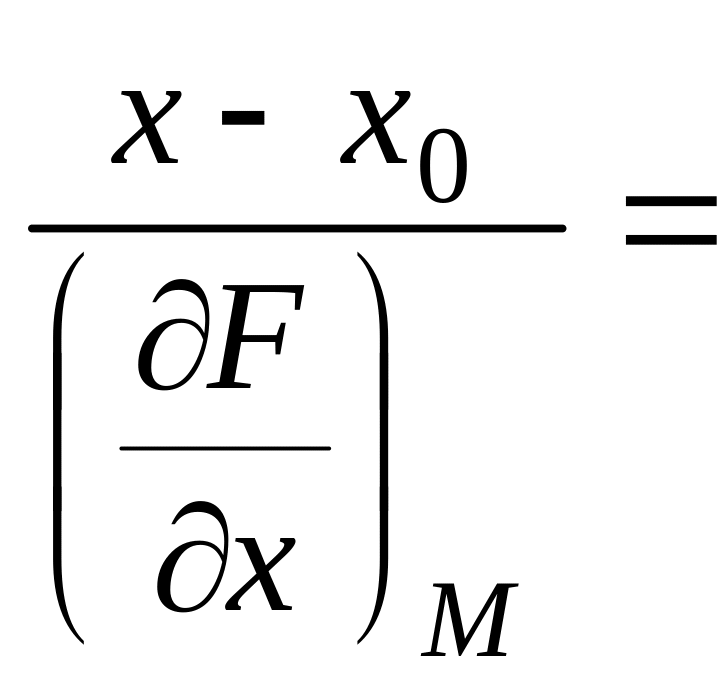
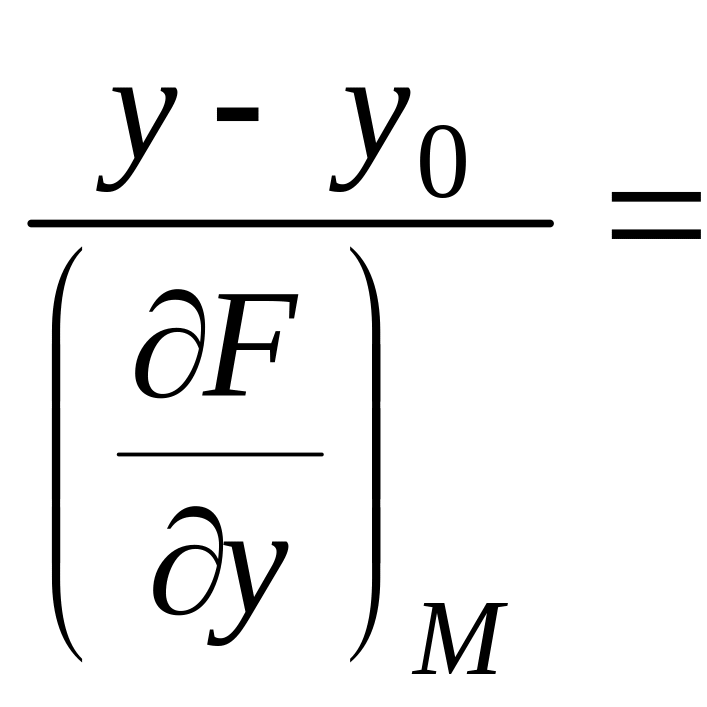
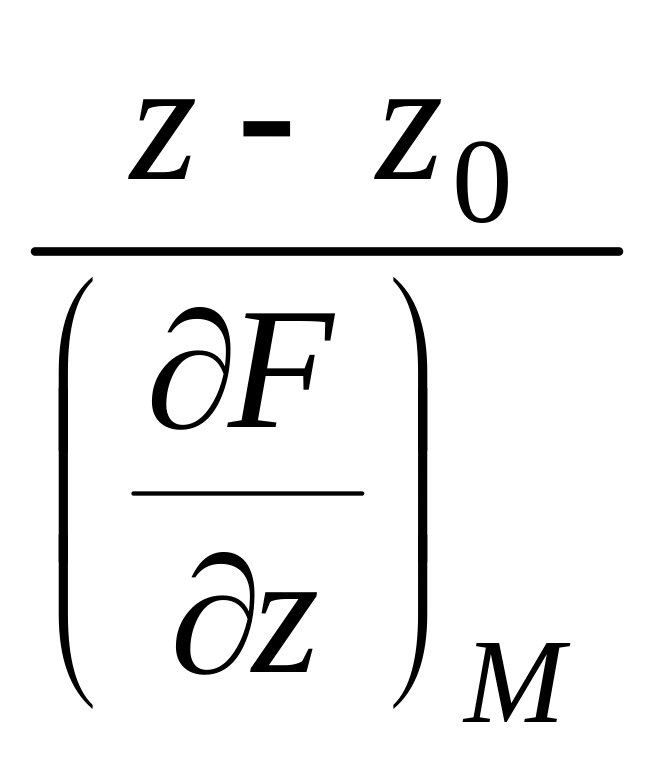. (3)

Если поверхность задана явно, т.е. уравнением

z = f(x, y),

то уравнение нормали имеет вид:

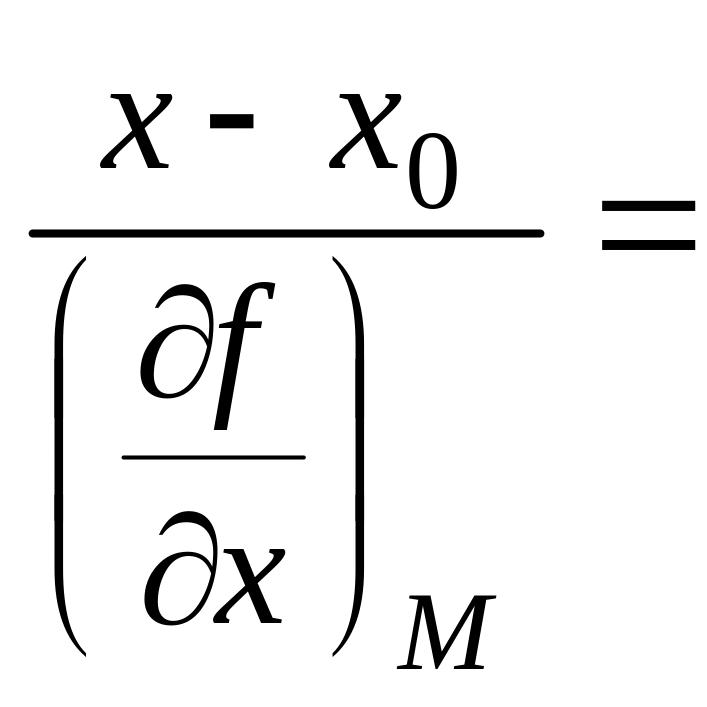
. (4)

Пример. Написать уравнения касательной плоскости и нормали к поверхности шара

х² + у² + z² = 14

в точке М(1; 2; 3).

□ а) Так как поверхность задана неявно, то уравнение касательной плоскости имеет вид:

.

Далее

F(x, y, z) = х² + у² + z² −14.

Тогда

, ,

и

, , .

Искомое уравнение касательной плоскости:

2(х – 1) + 4(у – 2) + 6(z – 3) = 0

или

х + 2у + 3z − 14 = 0.

В нашем случае уравнение нормали имеет вид:

.

Подставляя координаты точки и значения производных, получим

или

. ■