§ 22. Исследование поведения функций и построение графиков

1. Монотонность функции.

Теорема 1. Признак монотонности функции.

Если функция f(x) дифференцируема на интервале (a, b) и ≥ 0 ( ≤ 0) на (a, b), то функция f(x) не убывает (не возрастает) на (a, b).

○ Для определенности пусть ≥ 0. Пусть точки х₁,х₂ (a, b) произвольные и х₂ > х₁. Тогда на отрезке [х₁, х₂] выполняются условия теоремы Лагранжа, согласно которой

f(x₂) − f(x₁) = (х₂ − х₁), с ( х₁, х₂).

Так как ≥ 0 и х₂ − х₁ > 0, то f(x₂) − f(x₁) ≥ 0 или f(x₂) ≥ f(x₁). Это и означает, что функция f(x) не убывает на (a, b).

Аналогично доказывается случай ≤ 0. ●

Замечание. Точно также можно доказать, что если > 0 ( < 0) на (a, b), то f(x) возрастает (убывает) на (a, b).

Геометрический смысл.

Если функция f(x) не убывает на (a, b), то касательная к кривой у = f(x) в каждой точке на этом интервале образует с осью ОХ острый угол ( > 0 и > 0) или в отдельных точках параллельна оси ОХ:

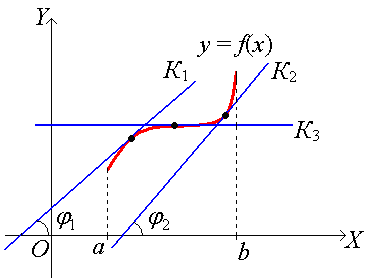
Если функция f(x) не возрастает на (a, b), то касательная к кривой у = f(x) в каждой точке на этом интервале образует с осью ОХ тупой угол ( < 0 и < 0) или в отдельных точках параллельна оси ОХ:

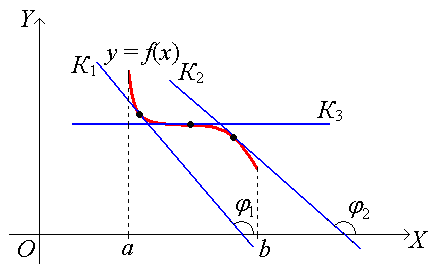
2. Экстремумы функции.

Точка х₀ называется точкой строгого локального максимума (минимума) функции f(x), если для всех х из некоторой -окрестности точки х₀ выполняется неравенство f(x) < f(x₀) (f(x) > f(x₀)) при х ≠ х₀.

Локальный максимум (max) и локальный минимум (min) объединяются общим названием локальный экстремум.

Экстремум имеет локальный (местный) характер, т.е. неравенство f(x) < f(x₀) (f(x) > f(x₀)) выполняется только в некоторой окрестности точки х₀. Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов на рассматриваемом интервале:

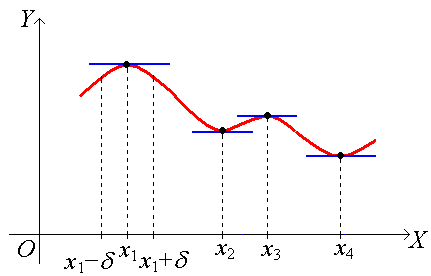
Теорема 2. Необходимое условие экстремума.

Если функция f(x) имеет в точке х₀ локальный экстремум и дифференцируема в этой точке, то = 0.

○ Так как в точке х₀ функция f(x) имеет локальный экстремум, то существует такой интервал (х₀− , х₀+ ), в котором значение функции f(x₀) является наибольшим (наименьшим) среди всех других значений этой функции. Тогда, согласно теореме Ферма, = 0. ●

Геометрический смысл.

Если х₁, х₂, х₃, х₄ – точки локального экстремума и в соответствующих точках графика существуют касательные, то они параллельны оси ОХ. Это видно на последнем рисунке.

Точка x₀, в которой = 0 может и не быть точкой экстремума.

Пример. □ Рассмотрим функцию f(x) = х³. Найдем производную = 3х². Производная = 0 при х = 0, но в точке х = 0 нет локального экстремума:

■

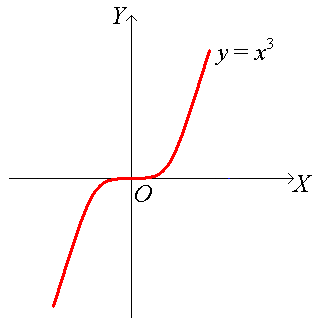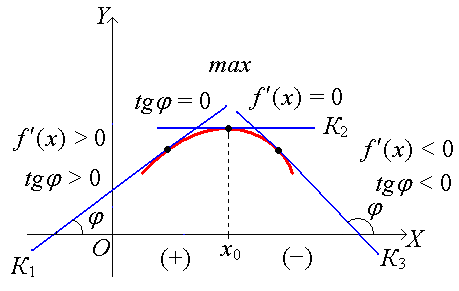
Теорема 3. 1-е достаточное условие экстремума.

Пусть функция f(x) дифференцируема в некоторой -окрестности точки х₀. Тогда, если > 0 ( < 0) для всех х (х₀ − , х₀), а < 0 ( > 0) для всех х (х₀, х₀+ ), то в точке х₀ функция f(x) имеет локальный максимум (минимум). Если же во всей -окрестности точки х₀ имеет один и тот же знак, то в точке х₀ локального экстремума нет.

Другими словами, если при переходе через точку х₀ меняет знак с + на −, то х₀ – точка локального максимума, если при переходе через точку х₀ меняет знак с − на +, то х₀ – точка локального минимума, если же знак в точке х₀ не изменяется, то в точке х₀ экстремума не существует.

○ Пусть при переходе через точку х₀ меняет знак с + на − и пусть х (х₀ − , х₀).

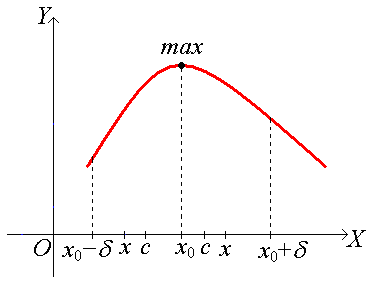
Используя формулу Лагранжа к функции f(x) на отрезке [x, х₀], получим

f(x₀) − f(x) = (х₀ − х), с ( х, х₀).

Так как > 0 на (х₀ − , х₀), то > 0 и, кроме того, х₀ − х > 0. Следовательно,

f(x₀) − f(x) > 0 или f(x₀) > f(x). (1)

Пусть теперь х (х₀, х₀+ ). Используя формулу Лагранжа к функции f(x) на отрезке [x₀, х], получим

f(x) − f(x₀) = (х − х₀), с ( х₀, х).

Так как < 0 на (х₀, х₀+ ), то < 0 и, кроме того, х − х₀ > 0. Следовательно,

f(x) − f(x₀) < 0 или f(x₀) > f(x). (2)

Из неравенств (1) и (2) следует, что в рассматриваемой окрестности точки х₀ выполняется неравенство f(x) < f(x₀) при х ≠ х₀, а это означает, что в точке х₀ функция f(x) имеет локальный максимум.

Аналогично рассматривается случай перемены знака с − на +.

Рассмотрим теперь случай, когда не меняет знака. Пусть > 0 в некоторой окрестности (х₀− , х₀+ ). По признаку монотонности функция не убывает на всей (х₀− , х₀+ ), т.е. для любых х < х₀ выполняется неравенство f(x) < f(x₀), а для любых х > х₀ − неравенство f(x) > f(x₀). Это и означает, что точка x₀ не является точкой локального экстремума. ●

Геометрический смысл:

Замечание 1. Теорема 3 справедлива, если функция f(x) в самой точке x₀ не дифференцируема, а только непрерывна. Примером является ранее рассмотренная функция у = | x |, которая в точке х = 0 непрерывна, не дифференцируема, но имеет минимум.

Точки, в которых производная равна нулю или не существует будем называть точками возможного экстремума (критические точки).

Теорема 4. 2-е достаточное условие экстремума.

Если = 0, а ≠ 0, то функция f(x) в точке x₀ имеет максимум при < 0 и минимум при > 0.

Теорема 5. 3-е достаточное условие экстремума.

Если = =…= = 0, а ≠ 0, то функция f(x) в точке x₀ имеет максимум при < 0 и минимум при > 0.

Замечание 2. Если требуется найти наибольшее значение непрерывной функции на отрезке [a, b], то следует:

1). найти все максимумы функции на отрезке;

2) определить значения функции на концах отрезка, т.е. вычислить f(а) и f(b);

3). Из всех полученных выше значений функции выбрать наибольшее; оно и будет представлять собой наибольшее значение функции на [a, b].

Аналогично определяется наименьшее значение непрерывной функции на отрезке [a, b].

3. Выпуклость, вогнутость и точки перегиба кривой.

График функции (кривая) у = f(x) называется выпуклым на интервале (a, b), если все его точки лежат ниже любой его касательной на этом интервале

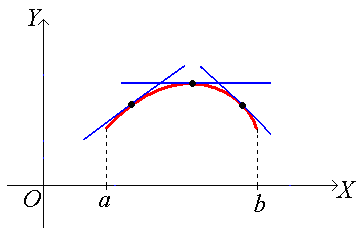
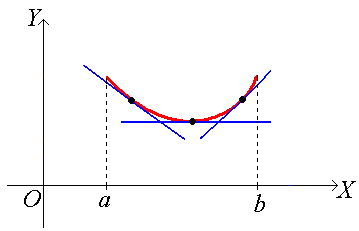
График функции (кривая) у = f(x) называется вогнутым на интервале (a, b), если все его точки лежат выше любой его касательной на этом интервале

Теорема 6. Если функция у = f(x) имеет на интервале (a, b) вторую производную и > 0 ( < 0) во всех точках (a, b), то график функции f(x) имеет на (a, b) вогнутость (выпуклость).

Точкой перегиба графика непрерывной функции у = f(x) называется точка графика М(x₀, f(x₀)), разделяющая выпуклую его часть от вогнутой

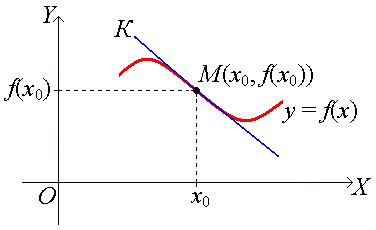
Теорема 7. Необходимое условие перегиба.

Пусть график функции у = f(x) имеет перегиб в точке М(x₀, f(x₀)) и пусть функция f(x) имеет в точке x₀ непрерывную вторую производную. Тогда = 0.

○ Предположим обратное, т.е. ≠0. Тогда, в силу непрерывности второй производной, существует окрестность точки x₀, в которой > 0 ( <0). Значит, согласно теореме 6, график функции у = f(x) в этой окрестности имеет вогнутость (выпуклость). Но это противоречит наличию перегиба в точке М(x₀, f(x₀)). Следовательно, = 0. ●

Отметим, что не всякая точка М(x₀, f(x₀)), для которой = 0, является точкой перегиба.

Пример. □ Рассмотрим функцию f(x) = х⁴. График этой функции не имеет перегиба в точке (0; 0), хотя = 12 х² = 0 при х = 0:

■

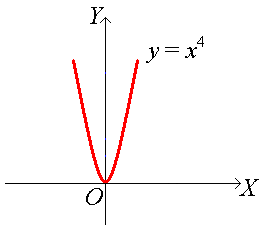Теорема 8. Достаточное условие перегиба.

Если вторая производная дважды дифференцируемой функции у = f(x) при переходе через точку x₀ меняет знак, то точка М(x₀, f(x₀)) есть точка перегиба ее графика.

○ Пусть < 0 слева от точки x₀ и > 0 справа от точки x₀. Тогда слева от x₀ график функции выпуклый, а справа – вогнутый (теорема 6). Значит, точка М(x₀, f(x₀)) с абсциссой x₀ есть точка перегиба графика функции у = f(x).

Аналогично рассматривается случай > 0 слева от точки x₀ и < 0 справа от точки x₀. ●

Замечание. Теорема справедлива, если функция f(x) в самой точке x₀ не имеет второй производной.

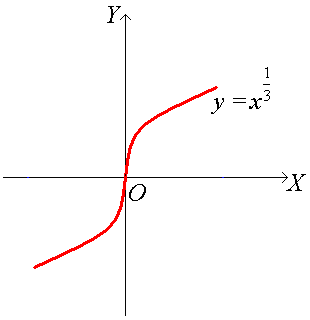
Пример. □ Рассмотрим функцию f(x) = . График этой функции имеет перегиб в точке (0; 0), хотя = 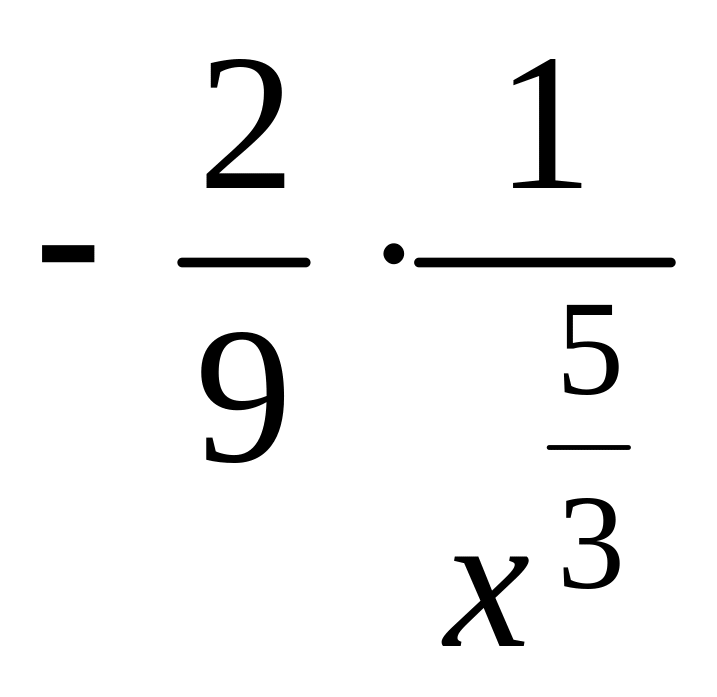не существует при х = 0:

■

Точки, в которых = 0 или не существует будем называть критическими точками (критические точки 2-го рода).

4. Асимптоты кривой.

Прямая называется асимптотой графика функции у = f(x), если расстояние d от точки М(x, f(x)) графика до этой прямой стремится к нулю при неограниченном удалении точки М кривой от начала координат

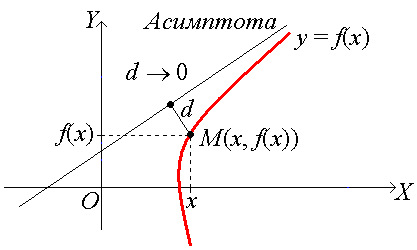
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.

Прямая х = x₀ называется вертикальной асимптотой графика функции у = f(x), если хотя бы один из односторонних пределов равен +∞ (−∞), т.е.

= +∞ (−∞) или = +∞ (−∞).

Прямая у = b называется горизонтальной асимптотой графика функции у = f(x) при ( ), если

= b.

Замечание 1. Если выполняется только

= b,

то говорят, что присутствует правая горизонтальная асимптота.

Если выполняется только

= b,

то говорят, что присутствует левая горизонтальная асимптота.

Пример. □ График функции у = f(x) =

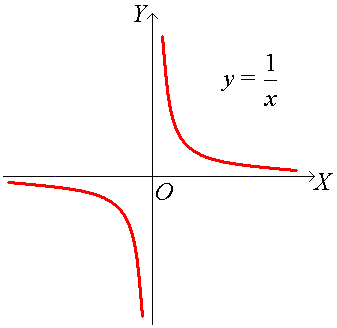
имеет вертикальную асимптоту х = 0, так как f(x) = → +∞ при х → 0+ и f(x) = → −∞ при х → 0−; график этой же функции имеет горизонтальную асимптоту у = 0 при х → ±∞, так как → 0 при х → ±∞. ■

Прямая у = kx + b (k ≠ 0) называется наклонной асимптотой графика функции у = f(x), если существуют пределы

k = , b =

или

k = , b = .

Целесообразно искать асимптоты в следующем порядке: вертикальные, горизонтальные, наклонные.

Общая схема исследования функций и построения их графиков

При исследовании функций и построении их графиков можно использовать следующую схему:

1. найти область определения функции;

2. исследовать функцию на четность-нечетность;

3. найти точки разрыва функции;

4. найти асимптоты графика функции;

5. найти интервалы возрастания и убывания, экстремумы функции;

6. найти интервалы выпуклости и вогнутости, точки перегиба графика функции;

7. найти точки пересечения графика функции с осями координат;

8. построить график.

Замечание 1. На практике удобно исследование функции проводить одновременно с построением ее графика.

Замечание 2. Исследование функции на четность-нечетность позволяет упростить общее исследование функции и построение ее графика.

Если функция f(x) четная (f(−x) = f(x)), то ее график симметричен относительно оси ординат (оси OY).

Если функция f(x) нечетная (f(−x) = − f(x)), то ее график симметричен относительно начала координат.

Если функция является четной или нечетной, то ее исследование достаточно провести, например, для х ≥ 0 [0, +∞). Для построения графика используют симметричность графика относительно оси OY или начала координат.

Если функция f(x) – функция общего вида (f(−x) ≠ ± f(x)), то ее исследование проводится на всей числовой оси (−∞, +∞).

Пример. Исследовать функцию и построить ее график:

.

□ Замечание. Удобно совмещать исследование функции с построением ее графика.

1. Область определения.

.

2. Четность – нечетность.

,

т.е. функция не является четной или нечетной. Следовательно, исследование необходимо провести на всей числовой оси (−∞, +∞).

3. Точки разрыва.

Числитель и знаменатель заданной функции непрерывные функции. Следовательно, функция будет разрывной только при х = 0, при котором знаменатель дроби обращается в ноль.

4. Асимптоты.

а) Вертикальные асимптоты.

;

.

Следовательно, прямая х = 0 – вертикальная асимптота. При этом, при приближении графика к вертикальной асимптоте слева и справа он стремится вверх ( значения функции стремятся к ).

б) Горизонтальные асимптоты.

= .

Это означает, что горизонтальных асимптот нет.

Наклонные асимптоты.

Наклонная асимптота имеет вид:

Найдем k и b:

k = 1,

b = .

Значит, наклонная асимптота имеет вид: у = х.

5. Возрастание, убывание. Экстремумы.

Найдем первую производную:

не существует : х = 0.

Функция не определена при х = 0. Следовательно, имеется одна точка возможного экстремума х = 2.

Выносим точки на числовую ось:

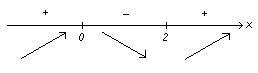
Определим знаки производной в интервалах:

: пусть , тогда

,

т.е. на этом интервале функция возрастает;

: пусть , тогда

,

т.е. на этом интервале функция убывает;

: пусть , тогда

,

т.е. на этом интервале функция возрастает.

Слева от критической точки х = 2 , а справа . Следовательно, х = 2 – точка минимума и

.

6. Выпуклость, вогнутость. Точки перегиба.

Найдем вторую производную:

= .

Вторая производная при любых допустимых значениях х положительная и не существует при х = 0. Функция не определена при х = 0. Следовательно, график функции вогнутый на интервалах и :

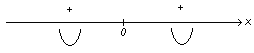
7. Точки пересечения с осями координат.

С осью Ох : у = 0, , , . Значит, точка пересечения графика функции с осью Ох.

С осью Оу : х = 0 – не входит в область определения функции, т.е. пересечения графика функции с осью Оу нет.

График функции показан на рисунке:

■

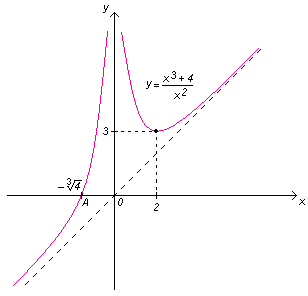Пример. Исследовать функцию и построить ее график:

.

□ Замечание. Удобно совмещать исследование функции с построением ее графика.

1. Область определения.

.

2. Четность – нечетность.

т.е. функция нечетная и ее график симметричен относительно начала координат.

Следовательно, достаточно исследовать функцию на интервале , построить график функции для этого интервала и отобразить его симметрично начала координат на левую полуплоскость.

3. Точки разрыва.

Функция непрерывна на всей числовой оси.

4. Асимптоты.

а) Вертикальные асимптоты.

Вертикальных асимптот нет, так как функция определена при всех действительных значения х .

б) Горизонтальные асимптоты.

= = = 0.

Следовательно, прямая у = 0 является горизонтальной асимптотой справа. В силу нечетности функции прямая у = 0 является горизонтальной асимптотой слева.

в) Наклонные асимптоты.

Наклонная асимптота имеет вид:

Найдем k и b:

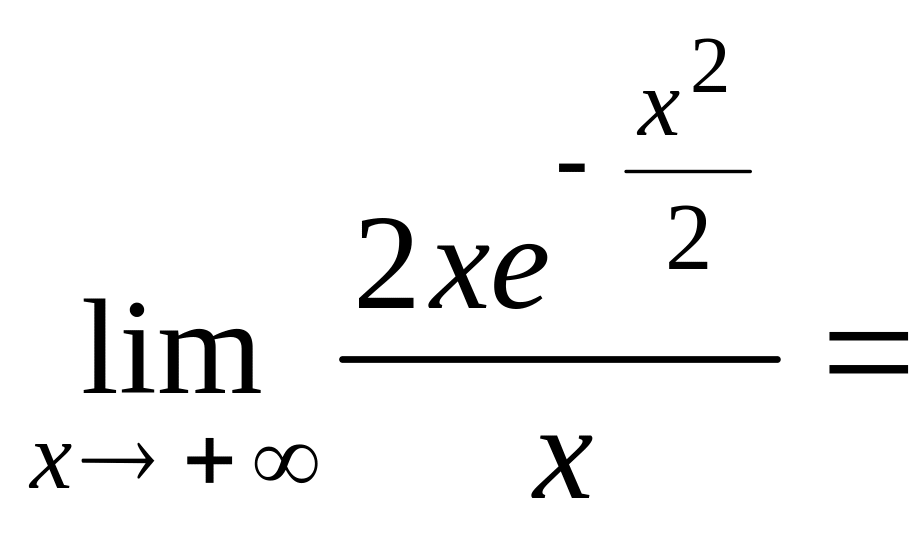
k = 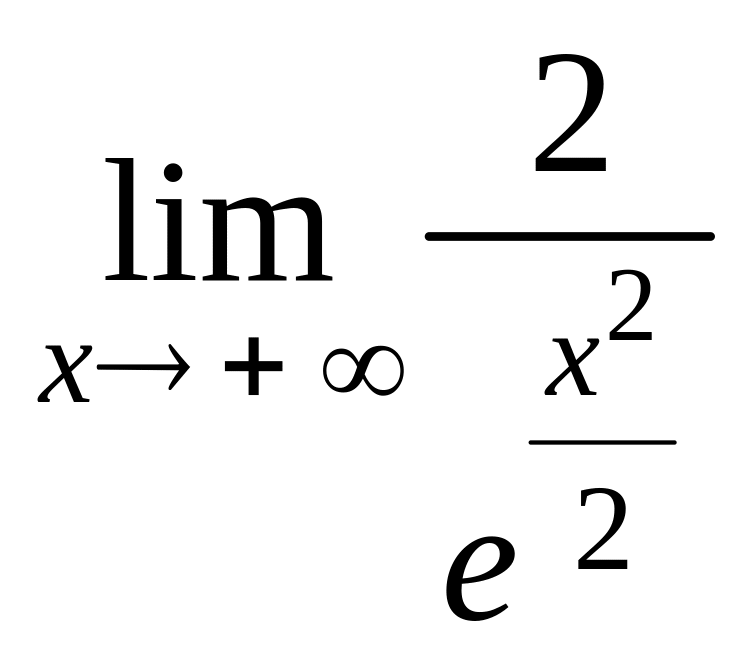= 0.

Следовательно, наклонных асимптот нет.

5. Возрастание, убывание. Экстремумы.

Найдем первую производную:

.

= 0, = 0, .

не существует : существует при любых действительных значениях х .

Значит, точки возможного экстремума: х₁ = 1 и х₂ = −1.

Выносим точку х₁ = 1 на числовую ось ( исследование проводим на интервале ):

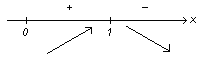
Определим знаки производной в интервалах:

: пусть , тогда

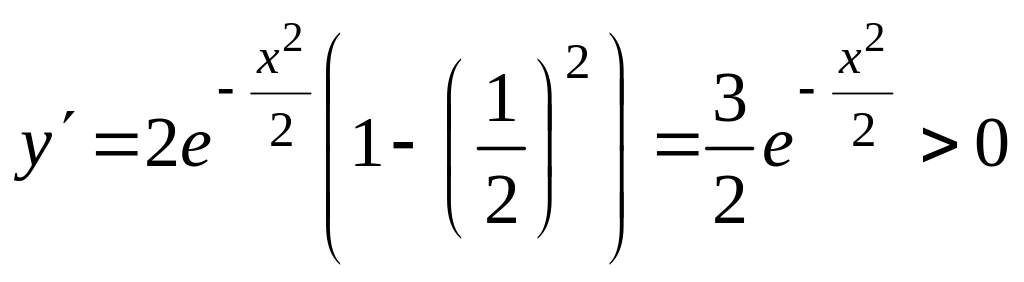
( показательная функция у = е^х всегда положительная ). Значит, функция на этом интервале возрастает. В силу нечетности функция возрастает и на ближнем слева от нуля интервале;

: пусть , тогда

,

т.е. на этом интервале функция убывает.

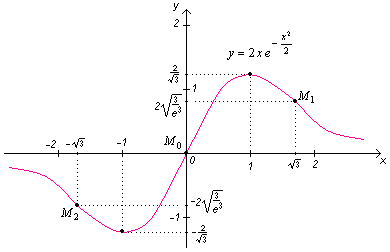
Слева от критической точки х = 2 , а справа . Следовательно, х = 1 – точка максимума и

.

В силу нечетности функции в критической точке х = −1 функция имеет минимум

.

6. Выпуклость, вогнутость. Точки перегиба.

Найдем вторую производную:

= = .

= 0, = 0, , .

не существует : существует при любых действительных значениях х .

Найденные точки – критические точки. Выносим их на числовую ось (исследуем интервал ) :

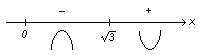
Определим знаки второй производной в интервалах:

: пусть , тогда

.

Следовательно, на этом интервале график функции выпуклый. В силу симметрии относительно начала координат на интервале слева от критической точки х₁ = 0 график функции вогнутый. Значит, критическая точка х₁ = 0 является абсциссой точки перегиба. Найдем ее ординату:

,

т.е. точка точка перегиба графика заданной функции.

Далее,

: пусть , тогда

.

Значит, на этом интервале график функции вогнутый. Так как слева и справа от критической точки вторая производная имеет разные знаки, то абсцисса точки перегиба. Найдем ее ординату:

,

т.е. точка точка перегиба графика функции.

В силу нечетности функции критическая точка абсцисса точки перегиба и точка

точка перегиба графика заданной функции.

Построив график функции для интервала и отобразив его симметрично начала координат на левую полуплоскость, получим график заданной функции :

■