§ 17. Основные теоремы дифференциального исчисления
Теорема Ферма. Пусть функция f(x) определена на интервале (a, b) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х0 существует производная, то = 0.
○ Пусть для определенности f(x) в точке х0 имеет наибольшее значение, т.е. f(x) ≤ f(x0) для х (a, b). Это означает, что
Δу
=
−
≤ 0
для
любой точки
(a,
b).
Поэтому, если Δх
> 0 (x
> x0),
то
≤ 0 и, следовательно,
= ≤ 0,
Если же Δх < 0 (x < x0), то ≥ 0, поэтому
= ≥ 0,
т.е. правая производная в точке x0 неположительна, а левая − неотрицательна. По условию, существует и, значит,
= = .
Это возможно только в случае, когда
= = 0.
Но тогда и = 0.
Аналогично доказывается случай, когда f(x) в точке х0 имеет наименьшее значение. ●
Геометрический смысл: если в точке х0 дифференцируемая функция f(x) имеет наибольшее (наименьшее) значение, то в точке (х0; f(x0)) касательная к графику функции f(x) параллельна оси ОХ
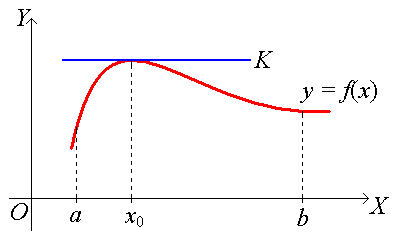
Теорема Ролля. Пусть на отрезке [a, b] определена функция f(x), причем:
1. f(x) непрерывна на [a, b];
2. f(x) дифференцируема на (a, b);
3. f(а) = f(b).
Тогда
существует точка с
(a,
b),
в которой
= 0.
○ Так как функция f(x) непрерывна на [a, b], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное значение т, т.е. существуют точки х1, х2 [a, b], в которых f(x1) = т и f(x2) = М и выполняются неравенства
т ≤ f(x) ≤ М.
Возможны два случая: 1. М = т, 2. т < M.
1. В этом случае f(x) = const = M = m. Следовательно, производная = 0 в любой точке отрезка [a, b] и теорема доказана.
2. В этом случае, так как f(а) = f(b), то хотя бы одно из двух значений т или М не принимается на концах отрезка [a, b], т.е. существует тоска с (a, b), в которой функция f(x) принимает наибольшее (наименьшее) значение на интервале (a, b). Тогда, так как f(x) дифференцируема в тоске с, из теоремы Ферма следует, что = 0. ●
Теорема Лагранжа. Пусть на отрезке [a, b] определена функция f(x), причем:
1. f(x) непрерывна на [a, b];
2. f(x) дифференцируема на (a, b).
Тогда существует точка с (a, b) такая, что справедлива формула
=
.
○ Введем в рассмотрение на [a, b] вспомогательную функцию
F(x) = f(x) − f(а) − (x – a).
Функция F(x) удовлетворяет условиям теоремы Ролля:
1. F(x) непрерывна на [a, b], как разность двух непрерывных функций;
2. F(x) дифференцируема на (a, b):
=
−
;
3. F(a) = F(b), т.к. F(a)= 0 и F(b)= 0.
Тогда,
по теореме Ролля, существует точка
с
(a,
b)
такая, что
=
0, т.е.
− = 0.
Отсюда получаем
= . ●
Замечание 1. Равенство
f(b) − f(а) = (b – a), а < c < b (1)
называется формулой Лагранжа или формулой конечных приращений.
Замечание 2. Так как точка с лежит между точками а и b, то можно записать
с
= а
+
(b
– a),
0 <
< 1.
Здесь (b – a) – часть длины отрезка [a, b]. Тогда формулу Лагранжа можно записать в виде
f(b)
− f(а)
=
(b
– a),
0 <
< 1.
Замечание 3. Если положить а = х, b = х + Δх, то получим
−
=
Δх,
0 <
< 1.
Такая запись формулы Лагранжа часто используется на практике.
Теорема Коши.
Пусть функции
и g(x)
непрерывны на [a,
b]
и дифференцируемы на (a,
b).
Пусть, кроме того,
≠ 0. Тогда существует точка с
(a,
b)
такая, что справедлива формула
=
.
(2)
○ Формула (2)
имеет смысл, если g(b)
≠ g(a).
Если предположить, что g(b)
= g(a),
то, по теореме Ролля, для функции g(x)
найдется точка
(a,
b),
в которой
=0.
Но это противоречит условию, что
≠ 0 на (a,
b).
Значит, формула (2) имеет смысл.
Рассмотрим на [a, b] вспомогательную функцию
F(x)= f(x)−f(а)− (g(x)–g (a)).
Функция F(x) удовлетворяет условиям теоремы Ролля:
1. F(x) непрерывна на [a, b];
2. F(x) дифференцируема на (a, b);
3. F(a) = F(b), т.к. F(a)= 0 и F(b)= 0.
Тогда существует точка с (a, b) такая, что = 0.
Так как
= − ,
то
=
−
= 0.
Отсюда, учитывая, что ≠ 0, получим
= . ●
Формула (2) называется формулой Коши или обобщенной формулой конечных приращений.
Замечание. Теорема Лагранжа является частным случаем теоремы Коши, если положить g(x) = х.