§ 13. Производные высших порядков
Пусть найдена производная функции f(x). Эту производную называют первой производной или производной первого порядка. В общем случае эта производная сама является функцией от х. Следовательно, ее можно дифференцировать:
=
− вторая
производная
или производная
второго порядка.
Эта производная, в общем случае, опять является функцией, т.е. ее можно дифференцировать:
=
− третья
производная
или производная
третьего порядка
и т.д.
Производной п-го порядка от функции f(x) называется производная от производной (п − 1)-го порядка этой функции
=
.
Обозначение:
, , , f IV(x), f V(x), f VI(x), …
или
, , , f (4)(x), f (5)(x), f (6)(x), … .
Пример. Найти производную четвертого порядка в точке х = 2 функции
у = .
□ Имеем
=
=
,
=
=
= −х−2,
=
=
2х−3,
=
= −6х−4
= −
;
(2)
= −
= −
= −
.
■
§ 14. Производные высших порядков от неявных функций
При нахождении производных высших порядков от неявной функции следует в выражение каждой последующей производной подставлять выражение первой производной от этой функции.
Пример.
Найти
функции
2у2 – 3х2 − = 0.
□ Найдем первую производную:
4у
− 6х
−
= 0,
= 6х,
=
=
.
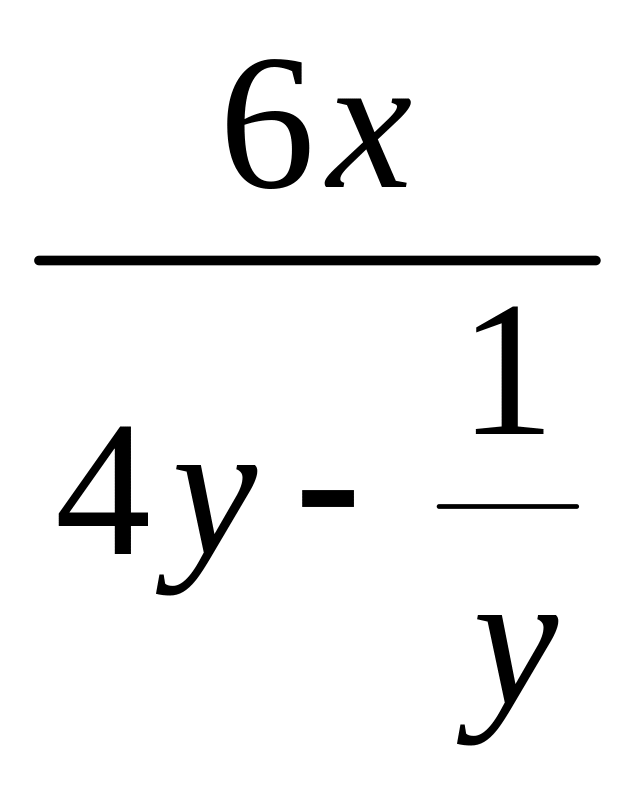Найдем вторую производную:
=
= 6·
= 6·
=
= 6·
=
6·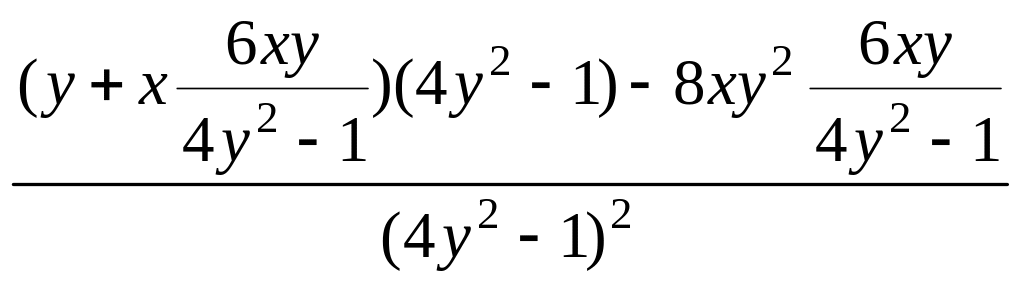
.
Упрощая, получим
=
.
■
§ 15. Производные высших порядков от функций,
ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Ранее было показано, что функция, заданная параметрическими уравнениями
х = , у = ,
имеет первую производную
= или = .
Заметим, что функция = , в свою очередь, задана параметрическими уравнениями
=
=
,
х
=
.
Тогда
=
=
=
=
,
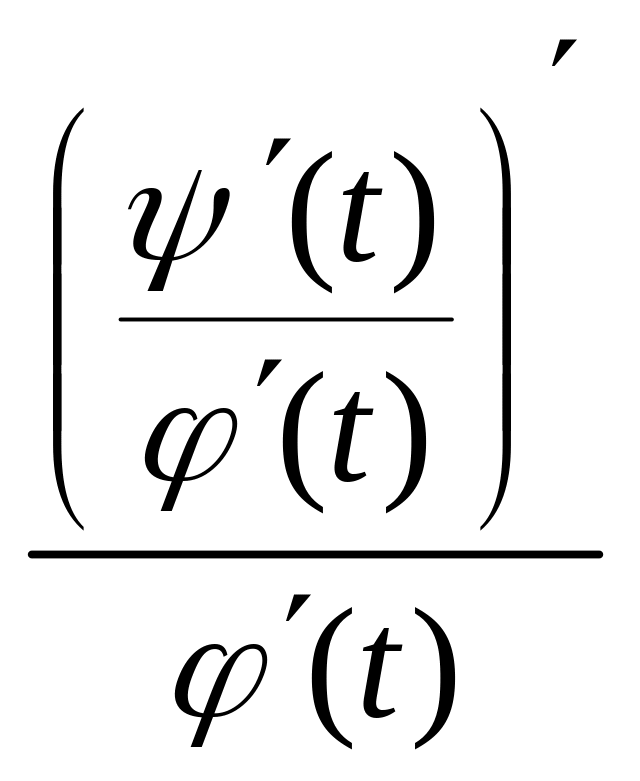т.е.
= .
Аналогично можно определить
=
и т.д.
Пример. Найти , , если
□ Найдем первую производную:
=
=
=
=
.
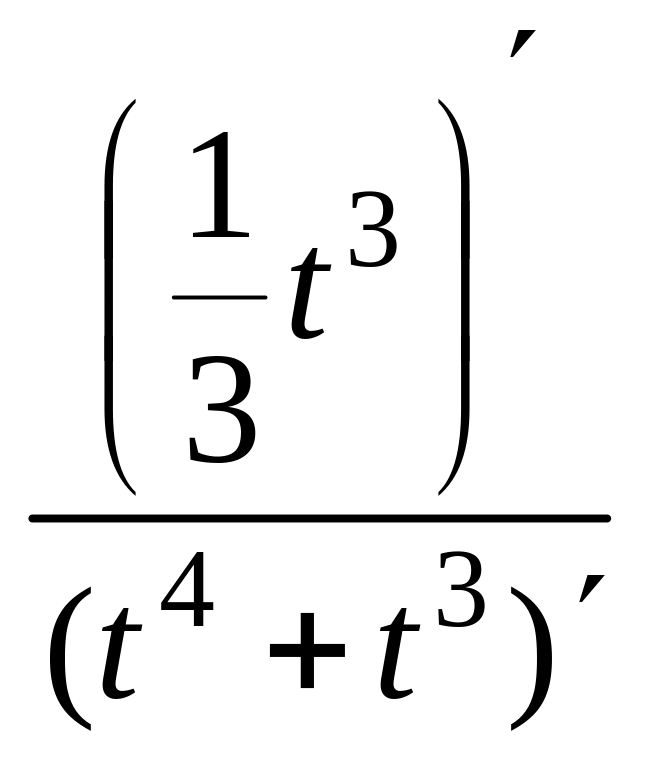Найдем вторую производную:
=
=
=
=
.
■
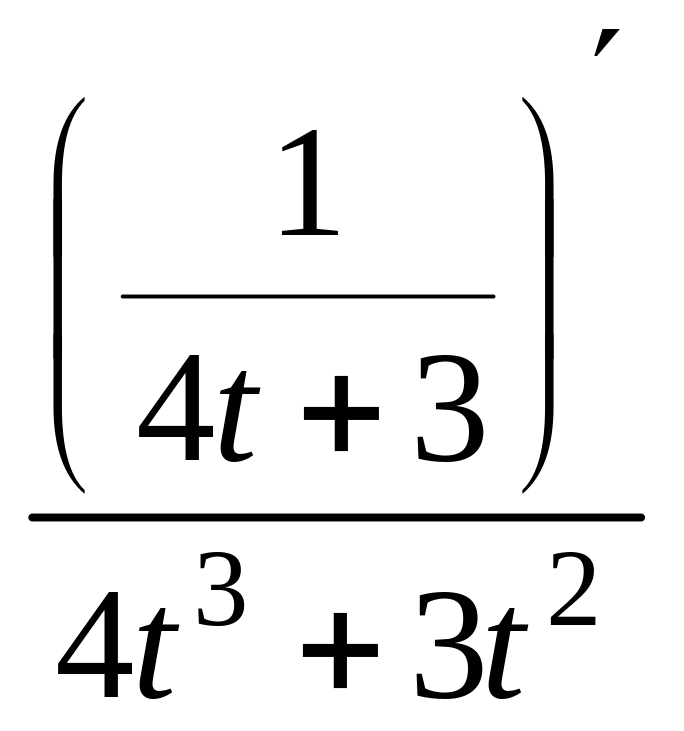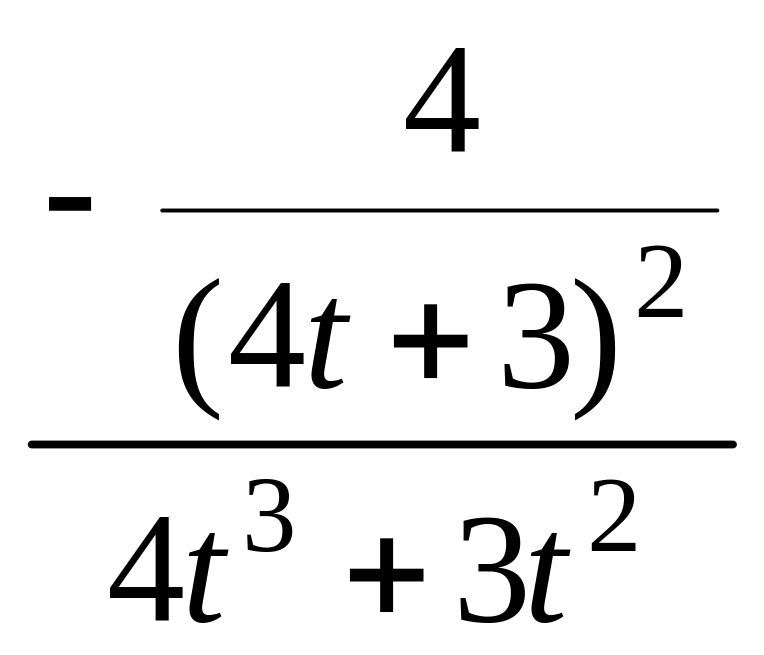§ 16. Дифференциалы высших порядков
Пусть имеем функцию у = f(x), где х – независимая переменная. Дифференциал этой функции dy = dx (первый дифференциал или дифференциал первого порядка) есть некоторая функция от х, но от х зависит только , а dx является приращением независимой переменной х и от х не зависит. Так как dy есть функция от х, то ее можно дифференцировать.
Дифференциал от дифференциала функции - второй дифференциал или дифференциал второго порядка:
d2y
= d(dy)
=
=
=
.
Третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
d3y
= d(d2y)
=
=
.
Дифференциалом п-го порядка называется дифференциал от дифференциала (п – 1)-го порядка функции у = f(x):
y
= d(
y)
=
=
,
т.е.
y = .
Пример. Вычислить дифференциалы dy, d2y, d3y функции
у = х4 – 3х2 + 4.
□ Последовательно дифференцируя, получим
dy
=
dx
=
= (4х3
– 6х)
dх;
d2y
=
= (12х2
– 6) dх2;
d3y
=
= 24х dх3.
■
Пример. Вычислить дифференциалы d2y функции
у = .
□ Имеем
y
=
.
Найдем производные и :
=
=
·
=
;
=
=
·
=
·
=
=
−
= −
.
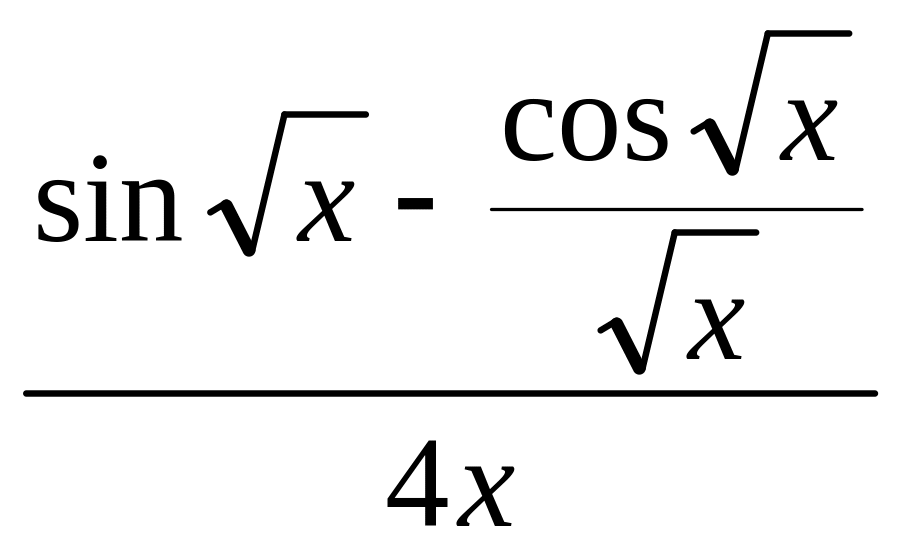Тогда
y
= −
.
■
Замечание. Дифференциал первого порядка имеет инвариантную форму, а второй дифференциал и последующие дифференциалы этим свойством уже не обладают.
Пользуясь дифференциалами различных порядков, можно записать производные различных порядков:
=
,
=
,
…,
=
.