§ 6. Производная степенной функции
Если у
=
,
где п
,
то
=
п
.
○ Имеем
у = ,
=
=
,
=
,
= п· ,
= y·
,
= · ,
т.е.
= = п . ●
§ 7. Производная показательной функции
Если у
=
(0 < а ≠
1), то
=
.
○ Имеем
у = ,
=
=
,
=
,
= ,
= y ,
т.е.
= = . ●
В
частности, если а
= е,
то
= 1 мы получаем для функции у
=
:
= = .
§ 8. Дифференцирование неявной функции
Пусть функция у, зависящая от х, задана в неявном виде, т.е. уравнением
F(x, y) = 0.
В некоторых случаях указанное уравнение удается разрешить относительно у, и тогда можно перейти от неявного способа задания функции к явному у = f(x). В других случаях такой переход оказывается неосуществимым
Пример. □ Функция х2 + у2 − а2 = 0 задана в неявном виде, но, решив это уравнение относительно у, получим функцию, заданную в явном виде:
у
= ±
и ее можно дифференцировать известным способом. Но неявную функцию
х2 − ху + = 0
нельзя записать в явном виде, но, тем не менее, ее можно продифференцировать. ■
Производная от неявной функции может быть определена следующим образом:
1. дифференцируем по х обе части уравнения F(x, y) = 0, рассматривая при этом у как функцию от х;
2. решаем полученное уравнение относительно .
В результате будем иметь выражение производной от неявной функции в виде
= f(x, y).
Пример. Найти производную функции
х2 − ху + = 0
и вычислить ее значение в точке (2;1).
□ Так как у является функцией от х, то будем рассматривать как сложную функцию от х. Продифференцировав по х обе части данного уравнения, получим
2х − у − х + = 0.
Решая последнее уравнение относительно , найдем выражение для искомой производной
= у
− 2х,
=
=
,
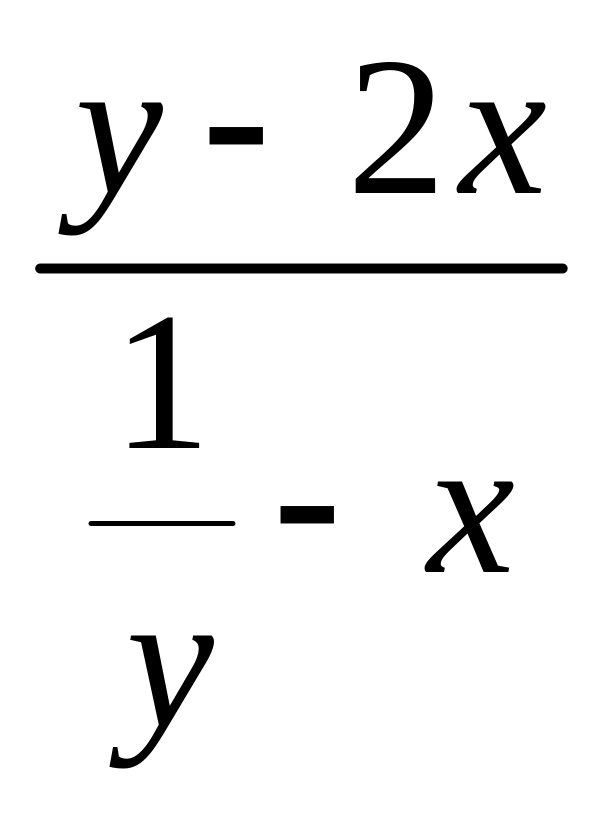т.е.
= .
Найдем значение производной при х = 2, у = 1:
=
=
= 3. ■
§ 9. Дифференцирование обратной функции
Теорема.
Если для функции у
= f(x)
существует обратная функция х
=
,
которая в рассматриваемой точке у
имеет производную
=
,
отличную то нуля, то в соответствующей
точке х
функция у
= f(x)
имеет производную
=
,
равную
=
(
=
).
○ Возьмем приращение , тогда
=
−
.
Так как есть функция монотонная, то ≠ 0. Напишем тождество
=
.
Так как непрерывна, то → 0 при → 0. Переходя к пределу при → 0 в првой части и при → 0 в левой части последнего равенства, получим
= или = . ●
Замечание. Можно обе части х = продифференцировать по х, считая у функцией от х. Тогда получим
1 = .
Отсюда
= .
§ 10. Производные обратных тригонометрических функций
Если у
=
,
то
=
.
○ Функция у
=
является обратной для функции х
=
.
Так как
=
,
то, по теореме о производной обратной
функции, получаем
=
=
=
.
Знак
перед корнем взят положительном, т.к.
положителен на интервале −
< y
<
.
Учитывая, что
= х,
получаем
= = . ●
Если у
=
,
то
= −
.
Доказательство аналогично предыдущему.
Если у
=
,
то
=
.
○ Функция у
=
является обратной для функции х
=
.
Так как
=
,
то
=
=
.
Но
= 1 +
= 1 + х2.
Следовательно,
= = . ●
Если у
=
,
то
= −
.
Доказывается аналогично предыдущему.