Элементы теории погрешностей

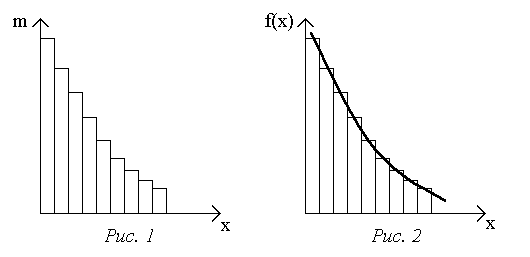Пусть имеется некоторая случайная величина х, которая может принимать непрерывный ряд значений. Будем считать, что такой величиной являются серии n измерений какой-то физической величины. Их можно наглядно представить, построив диаграмму, которая показывала бы, как часто получались при измерениях те или иные значения. Для этого весь диапазон измеренных значений, отложенных по оси Ох, разбивают на равные интервалы, ширина которых х может быть любой и выбирается так, как это удобно. Затем подсчитывают число m значений измеренной величины, попавших в каждый интервал, и на каждом интервале строят прямоугольник с основанием, равным ширине интервала, и высотой, равной числу значений измеряемой величины, попавших в данный интервал.

В итоге получается диаграмма, изображенная на рис.1. Такая диаграмма называется гистограммой. Ее можно построить и несколько иначе, откладывая по оси Оу не n, а m/n, т.е. относительное число значений х, попавших в интервал х. Такая гистограмма будет иметь вид, сходный с первой.

Предположим, что число измерений n велико. Ширину интервала можно сделать очень малой, если позволяет чувствительность измерительного прибора и в каждом интервале достаточно измерений. В пределе, уменьшая х и увеличивая n, вместо гистограммы получают плавную кривую (рис.2), характеризующую долю полного числа измерений случайной величины, значения которой попадают в каждый интервал. Такая кривая называется кривой распределения случайной величины, а функция у = f(х), описывающая эту кривую, – плотностью вероятности данного распределения или функцией распределения вероятностей.

Существуют различные виды распределения случайных величин. Однако особое значение в теории вероятностей и в практике измерений имеет нормальный закон распределения случайной величины (закон Гаусса), для которого функция распределения вероятностей описывается формулой

, (1)

где – математическое ожидание случайной величины;  – среднее квадратичное отклонение.

В теории погрешностей: – среднее арифметическое значение случайной величины;  – средняя квадратичная погрешность (нормальная ошибка измерений).

Случайные погрешности измерения подчиняются нормальному закону распределения в том случае, если наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение, а также если выполняются следующие требования:

1. погрешности измерения принимают непрерывный ряд значений;

2. при большом числе измерений одинаковые погрешности, но противоположного знака, равновероятны;

3. с увеличением погрешности вероятность ее уменьшается.

Возможны и другие виды распределения случайных погрешностей измерений, но нормальный закон встречается наиболее часто. Его особое значение определяется следующим обстоятельством: если случайная погрешность появляется в результате совместного действия нескольких причин, каждая из которых вносит малую долю в общую погрешность, то, по какому бы закону ни распределялись погрешности, вызванные каждой из причин отдельно, результат их суммарного действия привет к нормальному закону распределения результирующей случайной погрешности.

Зная закон распределения случайной погрешности, можно провести вероятностную оценку погрешности измерения. Проведем эту оценку для нормального распределения погрешностей измерения.

Пусть проделано n измерений некоторой величины х. В результате получен ряд значений этой величины: х₁, х₂, х₃, …, х_n. Наиболее вероятным является среднее арифметическое значение этой величины :

. (2)

Величина называется абсолютной погрешностью отдельного измерения. Среднее арифметическое значение абсолютных погрешностей отдельных измерений называется средней арифметической погрешностью :

. (3)

Качество результатов измерения характеризуют отношением средней арифметической погрешности к среднему арифметическому значению измеряемой величины. Это отношение называют относительной погрешностью Е:

. (4)

Средняя квадратичная, или стандартная, погрешность отдельного измерения равна

. (5)

Если число измерений велико, то  стремится к некоторому постоянному значению, квадрат которого называется дисперсией измерений:

D = ². (6)

Удобство оценки погрешности измерений с помощью средней квадратичной погрешности заключается в том, что  является параметром в нормальном законе распределения [см. (1)]. Значит, используя формулу (1), можно вычислить коэффициент надежности, или доверительную вероятность. Этот коэффициент показывает вероятность того, что результат измерения отличается от истинного значения не больше чем на х:

. (7)

Интервал значений измеряемой величины от до называется доверительным интервалом.

Таким образом, для характеристики случайной погрешности измерения необходимо указать две величины: саму случайную погрешность х и доверительную вероятность ее .

Результаты вычисления  по формуле (7) приведены в Приложении 1. В нем для любого х, выраженного в долях , т.е. для указаны значения вероятности.

Очевидно, чем больше х, т.е. чем больше , тем больше вероятность того, что значение измерения попадет в интервал от до . И наоборот, если уменьшать значения х, то вероятность попадания в этот интервал измерений будет уменьшаться.

Как видно из Приложения 1, вероятность того, что результат отдельного измерения отличается от истинного значения не более чем на х = , т.е. для  = 1, равна 0,68. Это значит, что 68% случайных погрешностей меньше , а остальные 32% больше . Если х = 2, т.е.  = 2, то вероятность того, что измерения будут отличаться от истинного значения не более, чем на 2, равна 0,95%, т.е. 95% случайных погрешностей меньше 2, а 5% больше 2. Для  = 3 величина  равна 0,997.

На рис.3 графически изображены приведенные соотношения для интервалов , 2, и 3. Заштрихованная площадь показывает доверительную вероятность для этих интервалов.

Средняя квадратичная погрешность [см. (5)] характеризует точность отдельного измерения. Погрешность же среднего арифметического значения величины S оказывается меньше, чем погрешность каждого отдельного измерения. Средняя квадратичная погрешность среднего арифметического значения связана со средней квадратичной погрешностью отдельного измерения соотношением

. (8)

Доверительную вероятность погрешности среднего арифметического значения можно также найти из Приложения 1. Для этого вместо  берут S, тогда

. (9)

Приведенные формулы и данные Приложения 1 оказываются справедливыми только для большого числа измерений. Однако не всегда можно провести достаточно большое число измерений. В этом случае для оценки доверительной вероятности случайных погрешностей нельзя пользоваться Приложением 1, так как эти погрешности распределены не по закону Гаусса, а по закону Стьюдента.

Для оценки доверительного интервала в случае небольшого числа измерений (n < 30) поступают следующим образом. Задав доверительную вероятность , находят по Приложению 2 значение коэффициента Стьюдента t_,n для данного числа измерений n. Эти коэффициенты играют ту же роль, что и , только определяются при небольшом числе измерений. При увеличении n значения коэффициентов Стьюдента приближаются к значению в Приложении 1. Определив по Приложению 2 t_,n , найдем

. (10)