Якщо розглядається задача на відшукання мінімального значення цільової функції, то формулюється така теорема.

Теорема 2.7. Якщо для деякого вектора виконується умова , то план не є оптимальним і можна побудувати такий план Х, для якого виконуватиметься нерівність .

Доведення аналогічне попередньому.

507. Знаходження оптимального розв'язку задачі лінійного програмування. Алгоритм симплексного методу.

Нехай невироджену задачу лінійного програмування представлено в канонічному вигляді:

,

де X = (x₁, …, x_n) — вектор змінних, C = (c₁, …., c_n), B = (b₁, …, b_m)^T, A_j = (a_1j, …, a_mj)^T, j = 1, …, n — задані вектори, T — знак транспонування, та

відмінні від нуля компоненти опорного плану, для полегшення пояснення розташовані на перших m місцях вектору X. Базис цього плану — . Тоді

, (1)

, (2)

де значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов A_j розкладається по них єдиним чином:

, (3)

, (4)

де x_ij коефіцієнт розкладання. Система умов

, (5)

z_k ≥ 0, x_j = 0, j = m + 1, …, n, j ≠ k (6) при заданому k визначає в просторі змінних задачі промінь, який виходить із точки, яка відповідає опорному плану, що розглядається. Нехай значення змінної x_k при русі по цьому променю дорівнює θ, тоді значення базисних змінних дорівнюють x_i(θ). В цих позначеннях рівняння (5) можна представити у вигляді

. (7)

помноживши рівняння (3) на θ при j = k та віднявши від рівняння (1), отримаємо

.(8)

Із рівнянь (7-8) отримаємо

. (9)

Оскільки x_i(θ) при θ = 0 визначають план задачі, то найбільше θ, яке не порушує обмеження x_i (θ) ≥ 0, визначається із умови

. (10)

де I = {i | x_ik > 0}.

В силу невиродженості задачі мінімум досягається не більш ніж для одного i = J та θ > 0. Значення лінійної форми при θ = θ₀ визначається із рівнянь (9), (4), (2)

,

де Δ_k = z_k — c_k. Очевидно, Δ_j = 0 для j = 1, …, m.

Нехай  — початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:

1. знайти Δ_k = min_jΔ_j. Якщо Δ_k = 0, тоді план, який розглядається оптимізовано; якщо Δ_k < 0, вектор A_k вводиться в базис;

2. знайти θ₀ та l, для якого 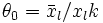, із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор A_l виводиться із базису;

3. за знайденими l, k обчислити нові значення елементів таблиці за формулами

(12)

,

де та перейти до виконання операції (1) з новими значеннями всіх x_ij = x'_ij.

508. Симплексний метод із штучним базисом. Ознака оптимальності плану із штучним базисом.

Розглянемо задачу лінійного програмування:

(2.60)

(2.61)

(2.62)

Задача подана в канонічному вигляді і система обмежень (2.61) не містить одиничної матриці. Отримати одиничну матрицю можна, якщо до кожного рівняння в системі обмежень задачі додати одну змінну . Такі змінні називають штуч­ними. (Не обов’язково кількість введених штучних змінних має дорівнювати m. Їх необхідно вводити лише в ті рівняння системи обмежень, які не розв’язані відносно базисних змінних.) Допустимо, що система рівнянь (2.61) не містить жодного одиничного вектора, тоді штучну змінну вводять у кожне рівняння:

(2.63)

У результаті додавання змінних у рівняння системи (2.61) область допустимих розв’язків задачі розширилась. Задачу з системою обмежень (2.63) називають розширеною, або М-задачею. Розв’язок розширеної задачі збігатиметься з розв’язком початкової лише за умови, що всі введені штучні змінні в оптимальному плані задачі будуть виведені з базису, тобто дорівнюватимуть нулеві. Тоді система обмежень (2.63) набуде вигляду (2.61) (не міститиме штучних змінних), а розв’язок розширеної задачі буде розв’язком і задачі (2.60)—(2.62).

Згідно з симплексним методом до базису вводять змінні, які покращують значення цільової функції. Для даної задачі на максимум вони мають його збільшувати. Отже, для того, щоб у результаті процедур симплексних перетворень виключалися з базису штучні змінні, потрібно ввести їх у цільову функцію з від’ємними коефіцієнтами. Тобто цільова функція набуде вигляду:

(У разі розв’язання задачі на відшукання мінімального значення цільової функції вводять коефіцієнти, які є досить великими числами. Цільова функція тоді має вигляд: ).

Припускається, що величина М є досить великим числом. Тоді якого б малого значення не набувала відповідна коефіцієнту штучна змінна , значення цільової функції буде від’ємним для задачі на максимум та додатним для задачі на мінімум і водночас значним за модулем. Тому процедура симплексного методу одразу вилучає відповідні змінні з базису і забезпечує знаходження плану, в якому всі штучні змінні .

Якщо в оптимальному плані розширеної задачі існує хоча б одне значення , то це означає, що початкова задача не має розв’язку, тобто система обмежень несумісна.

Для розв’язання розширеної задачі за допомогою симплексних таблиць зручно використовувати таблиці, оцінкові рядки яких поділені на дві частини-рядки. Тоді в (m+2)-му рядку записують коефіцієнти з М, а в (m+1)-му — ті, які не містять М. Вектор, який підлягає включенню до базису, визначають за (m+2)-м рядком. Ітераційний процес по (m+2)-му рядку проводять до повного виключення всіх штучних змінних з базису, потім процес визначення оптимального плану продовжують за (m+1)-им рядком.