533. Градієнтні методи розв'язання задач нелінійного програмування та їх класифікація.
Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише певне наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.
В основі градієнтних методів лежить основна властивість градієнта диференційовної функції — визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.
534. Метод Франка-Вульфа. Алгоритм розв'язування задачі нелінійного програмування.
Розглянемо метод Франка — Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.
Нехай необхідно відшукати max F=f(x1,x2,…,xn) за лінійних обмежень: Сума(j=1,n)aijxj<bi (i=1,m); xj>0 (j=1,n).
Допустимо, що Х0 — початкова точка, що належить множині допустимих планів даної задачі. В деякому околі цієї точки нелінійну цільову функцію замінюють лінійною і потім розв’язують задачу лінійного програмування. Нехай розв’язок лінійної задачі дав значення цільової функції F0, тоді з точки Х0 в напрямку F0 необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х1, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.
535. Сепарабельна функція та її властивості. Розв'язування задач нелінійного програмування методом кусково-лінійної апроксимації.
Нехай задані x1<x2<…<xn — точки зміни формул.
Як і всі кусково-задані функції, кусково-лінійну функцію зазвичай задають на кожному з інтервалів (-безкінечність;x1),(x1,x2);…(xn;+безкінечність) окремою формулою. Записують це у вигляді:
{k0x+b0, x<x1
f(x)={k1x+b1, x1<x<x2
{…
{knx+bn, xn<x
Якщо до того ж виконані умови узгодження aixi+bi=ai+1xi+bi+1=f(xi) при i=1,2,…,n, то кусково-лінійна функція буде неперервною. Неперервна кусково-лінійна функція називається також лінійним сплайном.
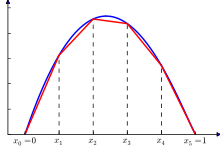
Функція (синя) і її кусково-лінійна апроксимація (червона).
536. Математична постановка задачі динамічного програмування, її економічний зміст. Принцип оптимальності Беллмана.
Динамічне програмування являє собою математичний апарат, що дає змогу здійснювати планування багатокрокових керованих процесів, а також процесів, які розвиваються у часі.
До задач динамічного програмування належать такі, що пов’язані з оптимальним розподілом капіталовкладень, розподілом продукції між різними регіонами, визначенням найкоротшого шляху завезення товарів споживачам, задачі щодо заміни устаткування, оптимального управління запасами тощо.
Економічні процеси можна уявити складеними з кількох етапів (кроків). На кожному з них здійснюється вплив на розвиток всього процесу. Тому у разі планування багатоетапних процесів прийняття рішень на кожному етапі має враховувати попередні зміни та бути підпорядкованим кінцевому результату. Динамічне програмування дає змогу прийняти ряд послідовних рішень, що забезпечує оптимальність розвитку процесу в цілому.
Ддля прийняття оптимального рішення на k-му кроці багатокрокового процесу потрібна оптимальність рішень на всіх його попередніх кроках, а сукупність усіх рішень дає оптимальний розв’язок задачі лише в тому разі, коли на кожному кроці приймається оптимальне рішення, що залежить від початкової суми, визначеної на попередньому кроці.
Цей факт є основою методу динамічного програмування і є сутністю так званого принципу оптимальності Р. Белмана, який формулюється так:
Оптимальний розв’язок багатокрокової задачі Х(х1,х2,…хn) має ту властивість, що яким би не був стан системи в результаті деякої кількості кроків, необхідно вибирати управління Xi+1 на найближчому кроці так, щоб воно разом з оптимальним управлінням на всіх наступних кроках приводило до максимального виграшу на всіх останніх кроках, включаючи даний.