3.1.4. Застосування функцій в економіці

Функція попиту - залежність попит на товар від ціни на нього:

де - попит на товар,

- ціна товару.

Функція чім попиту (залежність ціни від попиту):

Сумарний виторг продавця - це добуток кількості проданого товару на ціну р одиниці продукції.

Функція сумарного виторгу - це залежність між сумар­ним виторгом і кількістю проданного товару:

Функція пропозиції - залежність обсягу запропонованої продукції від ринкової ціни, тобто ціни від кількості:

де - обсяг пропозиції товару,

- ціна.

Функція ціни від пропозиції: .

Функція витрат - залежність між витратами на вироб­ництво деякої продукції і обсягом виробництва цієї продукції.

Якщо - сумарні витрати виробництва одиниць про­дукції, то функція сумарних витрат .

Зауваження. Функція - функція середніх витрат.

Взаємодія попиту і пропозиції на ринку приводить до рівноваги, при якій величини попиту і пропозиції рівні: .

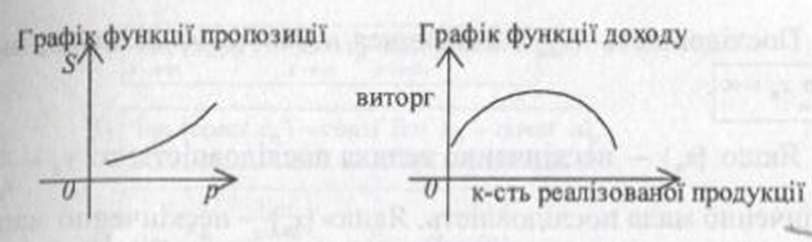
Функція доходу - залежність доходу від вартості вироб­леної продукції:

де - дохід,

- ціна одиниці продукції.

3.2. Границя функції. Неперервність функції

3.2.1. Поняття числової послідовності.

Приклади числових послідовностей

Якщо за деяким законом (правилом) кожному нату­ральному числу поставлено у відповідність деяке дійсне число , то кажуть, що задана числова послідовність

Числа - члени послідовності, - номер члена послі­довності.

Позначення числової послідовності: .

Приклади числових послідовностей:

1. 

2. 

3. 

3.2.2. Границя послідовності. Нескінченно малі та

нескін­ченно великі послідовності

Число називається границею послідовності . якщо для будь - якого існує таке натуральне число , що для всіх виконується нерівність . тобто .

Послідовність, що мас скінченну границю, називається збіжною, інакше - розбіжною

Послідовність називається нескінченно малою, якщо

її границя дорівнює нулю, тобто

Послідовність називається нескінченно великою, як­що

Якщо - нескінченно велика послідовність, то 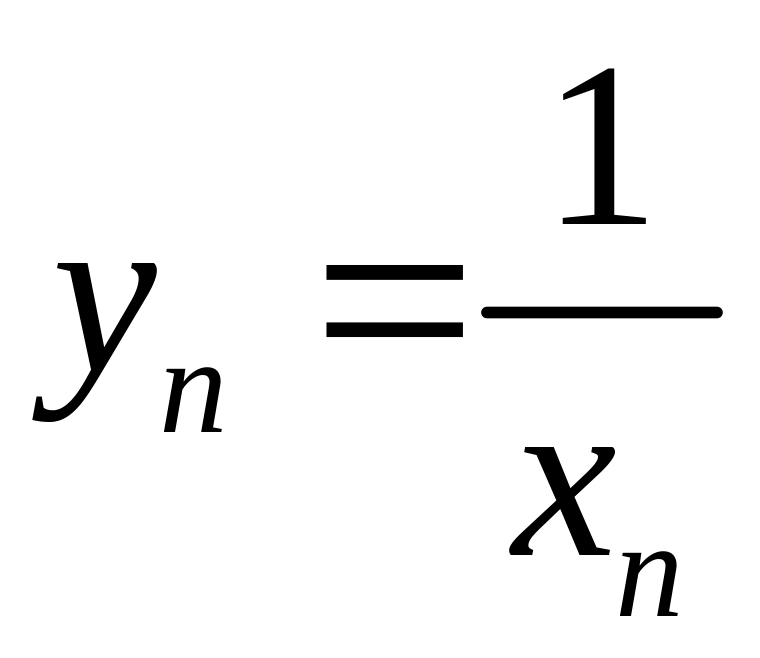— нескінченно мала послідовність. Якщо - нескінченно мала послідовність і , то послідовність нескінченно великою.

Послідовність називається обмеженою знизу (звер­ху), якщо існує таке число , що для всіх виконується нерівність .

Послідовність називається обмеженою, якщо існу­ють такі числа і , що для всіх виконується нерівність .

Наприклад. Послідовність натуральних чисел 1, 2, 3, ... обмежена знизу числом 1.

Послідовність називається зростаючою (спадною), якщо для будь-якого виконується нерівність .

Якщо , то послідовність називається строго зростаючою (спадною).

Наприклад. Послідовність є строго зростаю­чою.

3.23. Теореми иро границі

Теорема 1. Якщо послідовність мас границю, то така границя єдина.

Теорема 2. Якщо послідовності i збігаються, а також то послідовності також збігаються і вико­нуються рівності:

1. 

2. 

3. 

4. 

3.2.4. Приклади обчислення границь послідовностей

1. 

2. 

3.