3.2.1 Хаотические отклонения угловой частоты в двухмашинной ээс (случай 1)

Поставленная задача решается в предположении, что исходная двухмашинная ЭЭС – нерегулируемая. Такое допущение позволяет, с одной стороны, упростить систему нелинейных дифференциальных уравнений, описывающих состояние ЭЭС, а с другой стороны, дать качественный и количественный анализ получаемого хаотического решения для отклонений частоты в ЭЭС.

Математическая модель двухмашинной нерегулируемой ЭЭС, представленной в [35] , имеет вид:

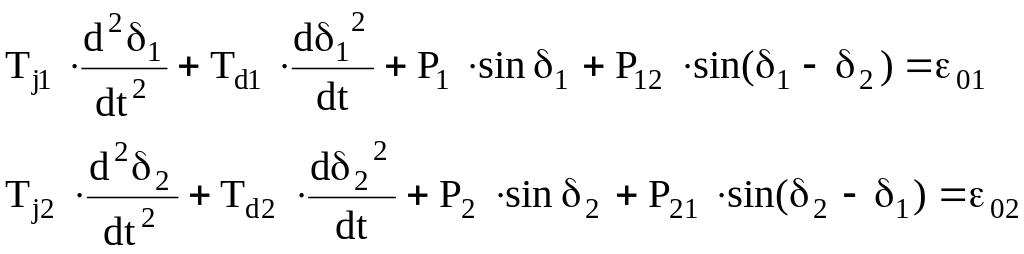, (3.2)

где – соответственно отклонения углов поворота роторов, постоянные инерции, коэффициенты демпфирования 1-го и 2-го генераторов,

Р_с12, Р_с21 – синхронизирующие мощности между генераторами,

– соответственно изменение мощности, выдаваемой в сеть 1-м и 2-м генераторами,

– соответственно начальные значения мощности, выдаваемой в сеть 1-м и 2-м генераторами при возникновении возмущения в сети.

Обозначим через соответственно отклонения угловой частоты (t) 1-го и 2-го генераторов. Тогда из системы дифференциальных уравнений (3.2) получим систему дифференциальных уравнений состояния ЭЭС в нормальной форме Коши

. (3.3)

Здесь – вектор переменных состояния и – совокупность параметров ЭЭС.

Двухмашинная нерегулируемая ЭЭС исследовалась с помощью программного комплекса MathCad . В программном комплексе MathCad ЭЭС задавалась в виде системы дифференциальных уравнений (3.3) и решение системы дифференциальных уравнений (3.3) проводилось методом Рунге-Кутта 4-го порядка с переменным шагом. Интегрирование (3.3) производилось при следующих значениях параметров ЭЭС в относительных единицах

и начальных условиях .

В результате обнаружены хаотические колебания отклонений углов поворота роторов и отклонений угловых частот генераторов ЭЭС, как это показано на рисунках 3.2, 3.3, 3.4. Необходимо отметить, что хаотические решения системы дифференциальных уравнений (3.3) получается лишь тогда, когда численные значения параметров ЭЭС лежат в строго определенных интервалах. Если это не выполняется, то решения системы дифференциальных уравнений (3.3) получаются нехаотическими.

Отсюда следует, что хаотические режимы ЭЭС возникают только при совпадении нескольких факторов, связанных с изменением численных значений параметров ЭЭС.

Фазовые портреты решений системы дифференциальных уравнений (3.3) представлены на рисунках 3.5, 3.6. Решение системы дифференциальных уравнений (3.3), отображенное на рисунке 5.4 представляет хаотические колебания отклонений угловой частоты с ярко выраженной расходимостью получаемых решений при незначительном отличии начальных условий.

При решении системы дифференциальных уравнений (3.3) обнаружено интересное явление – при превышении некоторого критического времени t  t_кр может происходить разрушение хаотического колебания с последующей потерей устойчивости генераторов ЭЭС. Соответствующее этому явлению решение системы дифференциальных уравнений (3.3) в виде временной зависимости и фазового портрета приведены на рисунках 3.7, 3.8. Заметим, что разрушение хаотических колебаний не носит обязательного характера.

Спектральный анализ хаотических колебаний и подтвердил предположение о широкополосном непрерывном спектре хаотических колебаний . Этого следовало ожидать, поскольку есть непериодические функции времени. Спектр хаотических колебаний представлен на рисунке 3.9 и его вид лишний раз свидетельствует о том, что колебания являются хаотическими .Исследование хаотических процессов ЭЭС и анализ следствий из них вытекающий, указывает на присутствие в теории детерминированного хаоса ЭЭС так называемого “эффекта бабочки”. К примеру, незначительные изменения начальных условий приводит с течением времени к непредсказуемому расхождению траекторий в фазовом пространстве ЭЭС. С этим же “эффектом бабочки” связана внезапная потеря устойчивости генераторов. Чем сильнее проявляется “эффект бабочки”, тем потенциально опаснее непредсказуемая ситуация, развивающаяся в ЭЭС. В сущности, обнаружена генетическая связь между “эффектом бабочки” и детерминированным хаосом и такая связь, как можно предположить, характерна не только для ЭЭС, но и в целом для нелинейных диссипативных систем любой природы.

В контексте нелинейной динамики хаотический режим означает длительно нерегулярные и случайные, но ограниченные траектории в фазовом пространстве ЭЭС, которые являются очень чувствительными к начальным условиям, и имеет широкополосный непрерывный спектр. Другими словами, траектория в фазовом пространстве, если она является хаотической, совершенно непредсказуема, даже когда траектория эволюционирует согласно детерминированной системе дифференциальных уравнений.Трудно разграничить явление возникновения устойчивых предельных циклов и явление возникновения хаотических аттракторов (фазовых портретов), проистекающих из-за наличия глобальной хаотической динамики ЭЭС и связанных с ней глобальных хаотических режимов.Идентифицировано существование хаотических режимов ЭЭС как дополнительного рабочего состояния ЭЭС даже тогда, когда существуют точки устойчивого равновесия. Хаотический режим может завершиться внезапной потерей устойчивости синхронных генераторов и, следовательно, ЭЭС в целом.

Хаотические режимы особенно затрудняют работу синхронных генераторов, поскольку хаотические режимы имеют широкополосный спектр частот и могут индуцировать гармоники тока и напряжения, опасные для функционирования синхронных генераторов.

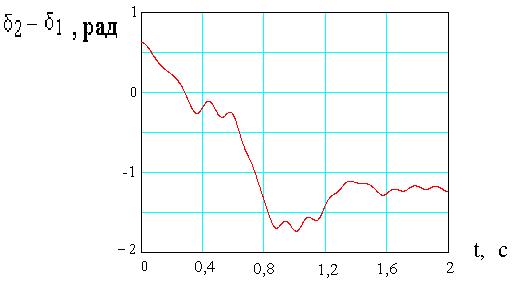
Рисунок 3.2 – Хаотический характер изменения разности отклонений углов поворота роторов генератора 2 и генератора 1

при начальных условиях (0.8, 0.1, 0.5,0.0)

Рисунок 3.3 – Хаотический характер отклонений угловой частоты генератора 1 с начальными условиями (0.8, 0.1, 0.5, 0.0)

Рисунок 3.4 – Хаотический характер отклонений угловой частоты генератора 2 с начальными условиями (0.8, 0.1, 0.5, 0.0) – непрерывная линия, с начальными условиями (0.7, 0.1, 0.5, 0.0) – пунктирная линия

Рисунок 3.5 – Фазовый портрет хаотической траектории в системе координат (δ₁, ω₁) при начальных условиях (0.8, 0.1, 0.5, 0.0)

Рисунок 3.6 – Фазовый портрет хаотической траектории в системе координат (δ₂, ω₂) при начальных условиях (0.8, 0.1, 0.5, 0.0)

Рисунок 3.7 – Потеря устойчивости хаотических колебаний при начальных условиях (0.8, 0.1, 0.5, 0.0)

Рисунок 3.8 – Фазовый портрет потери устойчивости хаотических колебаний при начальных условиях (0.8, 0.1, 0.5, 0.0)