2.5.3 Странные аттракторы

Математическим образом режима функционирования ДС служит аттрактор – предельное множество траекторий в фазовом пространстве системы, к которому стремятся все траектории из некоторой окрестности этого множества. Если это предельное множество есть устойчивое состояние равновесия – аттрактор системы будет просто неподвижной точкой, если это устойчивое периодическое движение — аттрактором будет замкнутая кривая, называемая предельным циклом. Раньше считалось, что аттрактор есть образ исключительно устойчивого режима функционирования системы. Сейчас мы понимаем, что режим детерминированного хаоса тоже аттрактор в смысле определения предельного множества траекторий в ограниченной области фазового пространства. Однако такой аттрактор имеет два существенных отличия: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима первоначально нарастают). Именно эти отличия и привели к необходимости ввести в рассмотрение новый термин – странный аттрактор.

Как установлено теоретиками, основным критерием “странности” аттрактора является неустойчивость траектории. Причем неустойчивость обязана быть экспоненциальной. Это означает, что малое возмущение режима D(0) должно во времени увеличиваться по экспоненте

D(t)= D(0) e^t , (2.43)

где  – показатель Ляпунова.

Оказалось, что положительность величины  говорит не только об экспоненциальной неустойчивости режима колебаний, но доказывает наличие в системе перемешивания. Если установлено, что исследуемый режим имеет положительный показатель Ляпунова  > 0, то следствием будут непериодичность в зависимости от времени любой из координат состояния, сплошной спектр мощности (в спектре колебаний присутствуют все частоты из некоторого интервала) и спадающая во време ни автокорреляционная функция. До недавнего времени с таким поведением указанных характеристик однозначно связывали представления о случайном процессе. Теперь мы знаем, что подобными свойствами может обладать процесс, порождаемый детерминированными законами. Это обстоятельство и послужило основанием называть такие процессы детерминированным хаосом.

2.6 Исследование свойств детерминированного хаоса. Характеристики хаотических режимов нелинейных электрических систем

Хаотические процессы в детерминированных нелинейных электрических системах (НЭС) – одна из фундаментальных проблем современного естествознания, являющаяся предметом пристального внимания исследователей. Убедительно доказано, что неустойчивость режима НЭС ведет к росту возмущений. Диссипативные НЭС вне зависимости от вида устойчивости вызывают уменьшение элемента фазового объема во времени до нуля, что связано с потерями энергии. Элемент фазового объема по некоторым направлениям должен растягиваться, а по другим сжиматься.

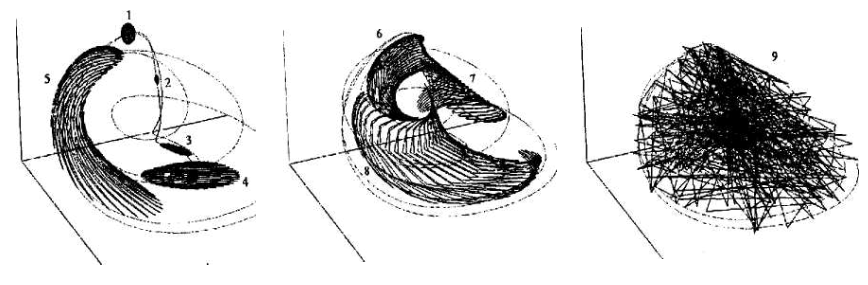
Рисунок 2.7 – Эволюция малого первоначального фазового объема 1 во времени в системе со странным аттрактором, иллюстрирующая перемешивание. Исходный объем 1 сжимается по одним и растягивается по другим направлениям (2, 3, 4), изгибается (5, 6), "складывается" (7, 8) и в итоге перемешивается по аттрактору (9)

Причем, степень сжатия в среднем должна обязательно превалировать над степенью расширения, чтобы в итоге фазовый объем во времени уменьшался. В диссипативных НЭС это оказывается возможным. В силу наличия механизма нелинейного ограничения фазовая траектория сложного режима колебаний сосредоточена в ограниченной области фазового пространства. При этом любая малая окрестность исходного начального состояния эволюционирует и в итоге перемешивается по всей области, занятой траекторией .

Таким образом, в неустойчивых режимах в детерминированных НЭС с перемешиванием однозначно можно предсказать будущее состояние только в случае строгого задания начальных условий. Однако, если учесть сколь угодно малую, но конечную ошибку, то детерминированное предсказание становится невозможным. Малая область первоначальной неопределенности размывается за счет перемешивания на конечную область в фазовом пространстве.

Обратимся к фазовому пространству R^N НЭС, зафиксировав значения всех параметров системы . Пусть имеется некоторая конечная область G1, принадлежащая R^N, которая включает в себя подобласть G₀.Области G₁ и G₀ удовлетворяют следующим условиям:

1. для любых начальных условий x_i(0) из области G₁ при (или n ) все фазовые траектории рано или поздно достигают области G₀;

2. область G₀ представляет собой минимальное компактное подмножество в фазовом пространстве НЭС;

3. если фазовая траектория принадлежит области G₀ в момент времени t = t₁ (n = n₁), то она будет принадлежать G₀ всегда, то есть для любых t > t₁ (n > n₁) фазовая траектория будет находиться в области G₀.

Если эти условия выполняются, то область G₀ называется аттрактором НЭС. Другими словами, аттрактор G₀ – это инвариантное минимальное предельное множество траекторий НЭС, куда стремятся и там остаются любые траектории из области G₁, охватывающей G₀. Область G₁ называется областью притяжения аттрактора G₀ .В области G₁ могут существовать исключительно переходные, нестационарные типы движений. Предельное множество G₀ отвечает установившимся типам движения [81].

Гомоклинические траектории Пуанкаре всегда имеют место в фазовом пространстве НЭС со стохастическим поведением. В их существовании кроется причина появления счетного множества седловых периодических движений, континуума устойчивых по Пуассону траекторий, счетного множества грубых гомоклинических траекторий, что и определяет в итоге чрезвычайно сложную картину разбиения фазового пространства на топологически различные типы ее движения. Именно с гомоклиническими эффектами связана возможность рождения динамической стохастичности, т.е. возникновение странного аттрактора .

Нерегулярные (хаотические) аттракторы требуют введения специальной классификации. Странные аттракторы можно разделить на три класса: гиперболические, аттракторы типа Лоренца и квазиаттракторы .

Гиперболические странные аттракторы – это грубые аттракторы, состоящие из множества неустойчивых по Ляпунову траекторий, которые всюду в любой произвольной точке аттрактора являются седловыми. Гиперболические аттракторы не могут включать регулярных, т.е. устойчивых, траекторий любого типа. Примером гиперболических аттракторов служат предельные множества Аносова, соленоиды Смейла-Вильямса и др.

Аттракторы типа Лоренца представляют собой негрубые предельные множества, в которых всюду плотные седловые периодические движения. Как и в гиперболических аттракторах, в аттракторах типа Лоренца при малых изменениях параметров и правых частей уравнений устойчивые периодические движения не возникают. Аттракторы типа Лоренца формируются в результате вполне определенного бифуркационного механизма и имеют характерную структуру. К настоящему времени аттракторы лоренцевского типа обнаруживаются в ряде НЭС при численном моделировании и с экспериментальной точки зрения являются наиболее близкими по своим свойствам к аттракторам гиперболического типа .

Однако наиболее часто встречающиеся в численных и физических экспериментах хаотические аттракторы относятся к третьему классу так называемых квазистохастических или просто квазиаттракторов. Квазиаттракторы являются сложными притягивающими предельными множествами, которые наряду с гомоклиническими структурами включают и устойчивые периодические аттракторы. Как правило, области притяжения регулярных аттракторов относительно малы, а характерные временные интервалы достаточно велики. При вариации параметров НЭС структура квазиаттракторов претерпевает цепочку сложных изменений, обусловленную бифуркациями регулярных и хаотических аттракторов. Причина этих изменений связана с тем, что в квазиаттракторе, наряду с грубыми гомоклиническими структурами, появляются и исчезают негрубые гомоклинические траектории седловых периодических колебаний.

Возникнув благодаря определенному бифуркационному механизму, странный аттрактор с изменением управляющих параметров НЭС может эволюционировать с сохранением первоначальной топологической структуры, но может демонстрировать и резкие ее изменения. Такие переходы в хаосе типичны в основном для квазиаттракторов. Причем квазиаттрактор может возникнуть при эволюции, например, аттрактора типа Лоренца с нарушением условий существования последнего .

По аналогии с эволюцией регулярных режимов при вариации параметров явление резкой перестройки геометрической структуры аттрактора при прохождении параметром критической точки можно назвать бифуркациями странных аттракторов.