2.4 Размерность предельных множеств

Для характеристики странных аттракторов целесообразно ввести понятие размерности. Размерность определяет количество информации, необходимое для задания координат точки, принадлежащей аттрактору, в рамках указанной точности. Для регулярных аттракторов, являющихся многообразиями, размерность – целое число: неподвижная точка имеет размерность 0, предельный цикл – 1, двумерный тор – 2 и т.д. Ввиду сложности геометрической структуры странные аттракторы не являются многообразиями и имеют дробную размерность .

Размерность – одна из фундаментальных характеристик аттрактора. В типичных случаях метрические размерности принимают одинаковую величину, которую принято называть фрактальной размерностью аттрактора D. Размерность, определяемую с учетом вероятности посещения траекторией различных областей аттрактора в фазовом пространстве, называют информационной или размерностью натуральной меры. Последняя, что важно для приложений, может быть оценена по спектру Ляпуновских характеристических показателей (ЛХП) аттрактора. Для типичных аттракторов информационная и ляпуновская (оцениваемая по спектру ЛХП) размерности обычно совпадают количественно, но могут отличаться от значений фрактальной размерности .

С помощью понятия размерности можно провести классификацию аттракторов. Действительно, любой аттрактор может быть назван n – мерным, если в произвольной окрестности каждой своей точки он подобен открытому подмножеству пространства Rⁿ. Например, в соответствии с таким определением предельный цикл является одномерным, поскольку локально он подобен интервалу. В свою очередь, тор является двумерным множеством, положение равновесия представляет собой множество нулевой размерности.

В противоположность этому, любая окрестность произвольной точки странного аттрактора имеет сплошную тонкую структуру и не может рассматриваться в качестве образа какого – либо евклидова пространства. Отсюда следует, что странные аттракторы не могут рассматриваться в качестве многообразий, а их размерность не может быть охарактеризована целым числом.

2.4.1. Фрактальная размерность

Идея, лежащая в основе понятия «фрактальная размерность», состоит в следующем. Произведем покрытие аттрактора А элементами объема, каждый из которых имеет диаметр . Через обозначим число элементов объема, необходимых для покрытия аттрактора А. при уменьшении диаметра элемента сумма элементов объема стремится к объему аттрактора А.

Если аттрактор А представляет собой некоторое D – мерное многообразие, тогда при заданном число элементов объема, необходимых для покрытия аттрактора А, будет обратно пропорционально . Другими словами, можно записать

, (2.36)

откуда размерность D равна

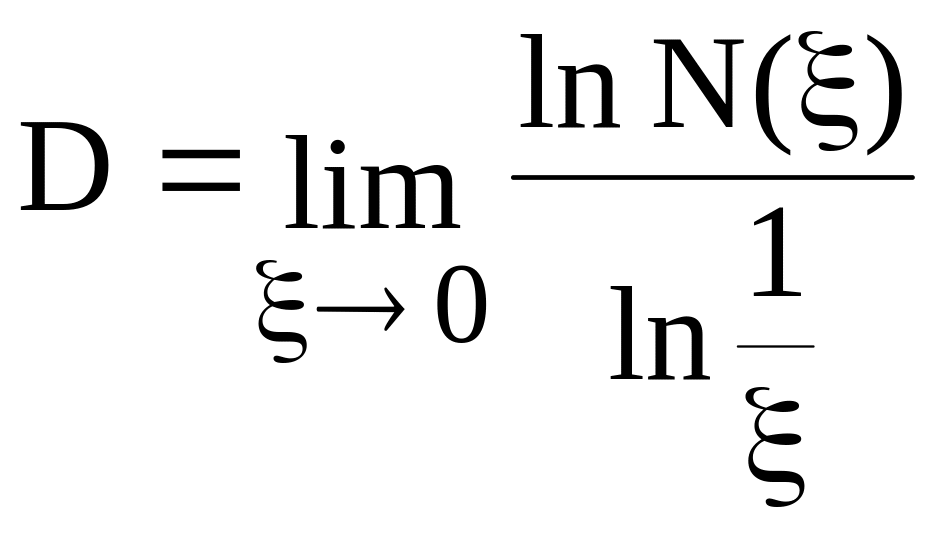. (2.37)

В тех случаях, когда этот предел не существует, размерность D не определена.В качестве простого наглядного примера приведем канторово множество. Это множество строится последовательным исключением открытых интервалов длиной 1/3 из середины закрытого (включающего граничные точки) единичного интервала. Выбросив первый раз среднюю треть, оставляем два закрытых интервала длиной в 1/3 каждый. Затем, выбросив средние трети из оставшихся двух отрезков, получим четыре закрытых интервала длиной 1/9 каждый. Канторово множество будет построено, если процесс исключения «ненужных» открытых интервалов продолжить до бесконечности, как схематически изображено на рис.3. На n-м шаге процедуры построения канторова множества останется разделенных между собой закрытых интервалов одинаковой длины .По определению найдем фрактальную размерность канторова множества:

.

Как впервые наблюдал в численном эксперименте М. Хенон, странные аттракторы имеют структуру типа канторовой..