Угловая нестабильность
Используем исходную модель ЭЭС и выбираем два начальных состояния, которые могут рассматриваться как два поствозмущенных состояния для исследуемой ЭЭС.
Случай 1: х1(0) = (1.140, 0, 1.055, 2.368, 1.100, 1.012)
Случай 2: х2(0) = (1.300, 0, 1.055, 2.368, 1.260, 1.012)
На рисунке2.19 показано решение для случая 1, на рисунке 2.20 показано решение для случая 2. Из рисунков 2.19 и 2.20, видно, что существуют очевидные угловые нестабильности без признаков лавины напряжения.
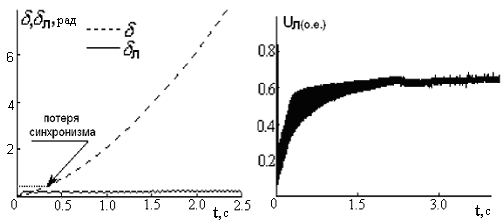
Рисунок 2.19 – Результаты моделирования случая 1
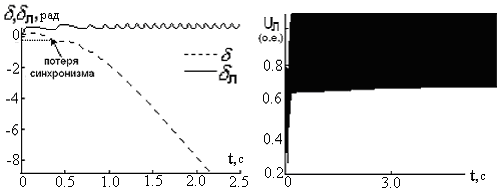
Рисунок 2.20 – Результаты моделирования случая 2
1.7.4 Неустойчивые режимы и хаос
Из вышесказанного становится ясным, что хаос может вызывать в ЭЭС лавину напряжения, угловую нестабильность или лавину напряжения с угловой нестабильностью одновременно. Поскольку хаос очень чувствителен к начальным условиям и параметрам ЭЭС, любое их изменение может привести к возникновению, либо прекращению режима хаоса. И в реальной ЭЭС все параметры изменяются с неожиданными вариациями, поэтому весьма вероятно существование хаоса в ЭЭС как промежуточной стадии явления нестабильности после большого возмущения.
Когда происходит возмущение, ЭЭС входит в переходное состояние. Если возмущение мало – может возникнуть бифуркация Хопфа, и следуют длительные колебания. Если возмущение большое, ЭЭС может входить в режим хаоса, но когда возмущение превышает некоторую критическую величину, хаотический режим может быть разрушен. Возможно появление лавины напряжения, угловой нестабильности или лавины напряжения и угловой нестабильности одновременно. Если возмущение очень большое, система может прямо прийти к вышеупомянутым трем условиям нестабильности по стадиям бифуркации Хопфа, хаоса и разрушения хаоса.
Рисунок ц.21 – Место хаоса в эволюции нестабильности ЭЭС
Отсюда следует, что хаотический режим может завершиться как устойчивым, так и неустойчивым состоянием.
На рисунке 2.22 показан в увеличенном масштабе фрагмент рисунка 2.11 Выберем пять точек равновесия 0, 1, 2, 3, 4 около бифуркации Хопфа (точка A) показанной на рисунке 2.22, где точка 0 слева от точки А – точка устойчивого равновесия, в то время как другие четыре точки – точки неустойчивого равновесия.
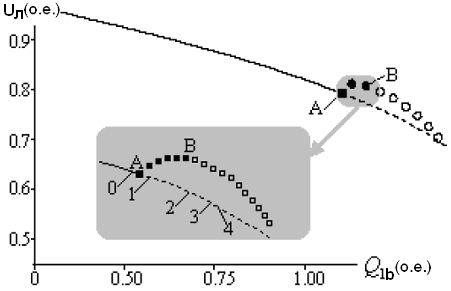
Рисунок 2.22 – Увеличенный масштаб рисунка 16
Если ЭЭС работает в точке 0, другие четыре точки могут рассматриваться как некоторые возможные состояния поствозмущения. Возмущение в точке 1 самое маленькое, в то время как возмущение в точке 4 максимальное. Выберем эти пять точек как начальные условия и интегрируем систему уравнений (2.55). Параметры, необходимые для интегрирования системы уравнений (2.55), приведены в таблице 2.1. Результаты показаны на рисунке 2.23.
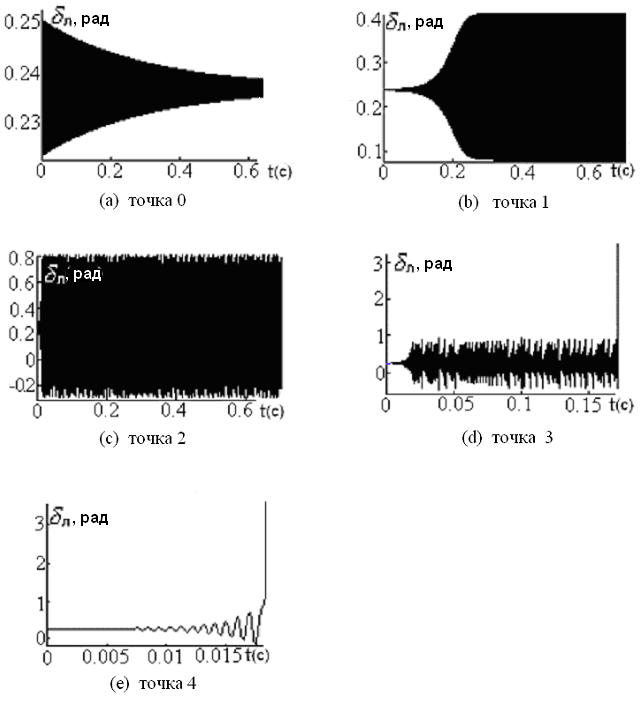
Рисунок 2.23 – Результаты моделирования
Очевидно, что, когда возмущение небольшое, в ЭЭС происходят периодические колебания так, как показано на рисунке 2.23b, которое вызвано бифуркацией Хопфа, или подвергается хаотическому колебанию, показанному на рисунке 2.23c. Когда возмущение возрастает, ЭЭС может подвергнуться нестабильности, вызванной разрушением хаоса, показанным на рисунке 2.23d или вернуться к нестабильности, как показано на рисунке 2.23e.