2.4.2 Информационная размерность

Понятие фрактальной размерности является чисто метрическим и никак не учитывает информацию о поведении динамической системы во времени. В отличие от этого понятие информационной размерности являются вероятностным и определяется через частоту попадания какой – либо траектории системы в заданную область. Понятие информационной размерности вводится с использованием той же процедуры построений, что и при определении фрактальной размерности. информационная размерность D_x задается выражением

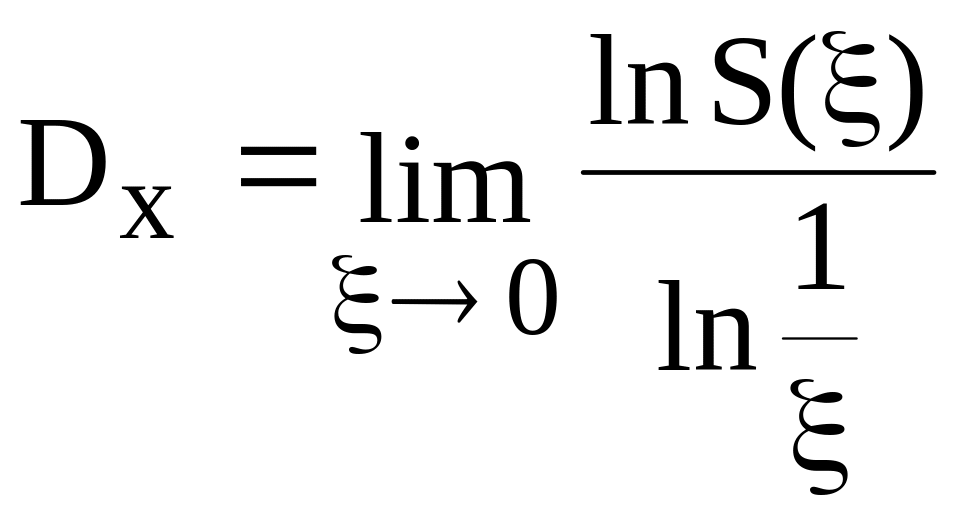, (2.38)

где .Величина P_i представляет собой относительную частоту, с которой некоторая типичная траектория попадает в i – элемент объема, а всего число таких элементов объема, покрывающих аттрактор А, равно . Величина представляет собой энтропию, т.е. количество информации, необходимое для задания состояния системы с точностью .

Удивительна на первый взгляд, но совершенно естественна при детальном рассмотрении взаимосвязь фрактальной размерности хаотического множества с показателями спектра ЛХП. Доказано, что для аттракторов двумерных обратимых отображений с постоянным якобианом преобразования справедливо соотношение

, ,

где определены соотношением (41). Если двумерное стохастическое множество в секущей Пуанкаре порождается соответствующим потоком, то в силу непрерывности потока (48) можно обобщить на случай трехмерных дифференциальных систем с отрицательной дивергенцией, не зависящей от фазовых координат:

, .

Здесь учитывается, что непрерывной траектории соответствует один нулевой показатель в спектре ЛХП.

2.4.3. Корреляционная размерность

Другим вероятностным типом размерности является корреляционная размерность D_c , которая определяется выражением

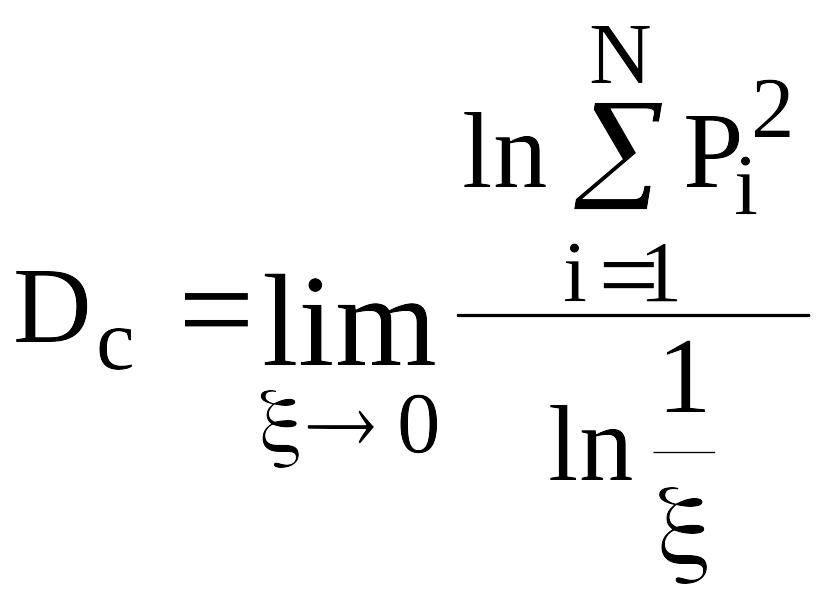, (2 ,39)

где , n_i – число точек, лежащих в i – м элементе объема, N – общее число точек. Для облегчения интерпретации числителя правой части предположим, что путем моделирования или в результате измерений были получены N точек на какой – либо траектории системы. Определим применительно к рассматриваемому случаю корреляционную функцию следующим образом:

.

Тогда выражение (47) может быть приведено к виду

.

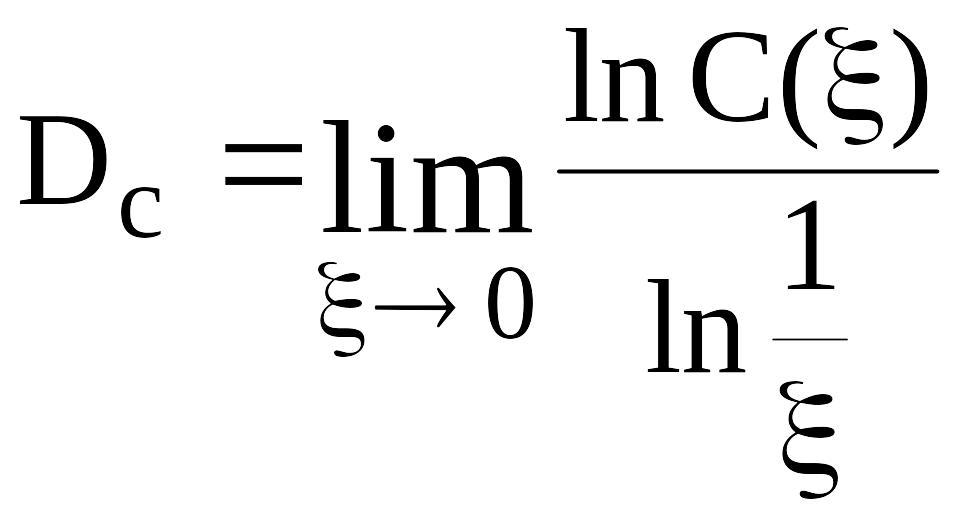2.4.4. Размерность по Ляпунову

Спектр ЛХП, являясь усредненной характеристикой аттрактора, описывает его свойства независимо от начальных условий из области притяжения. Исключением являются начальные данные, отвечающие неподвижным точкам, циклам и двоякоасимптотическим траекториям типа петель сепаратрис, имеющим отличающиеся ляпуновские показатели, а также траекториям, для которых спектр ЛХП вообще не определен. Полагается, что такие траектории имеют меру нуль (являются нетипичными), и это подтверждается численными экспериментами.

Определенные трудности возникают при теоретическом обосновании взаимосвязи фрактальной размерности со спектром ЛХП для многомерных (N > 3) систем, в которых степень сжатия фазового объема зависит от координат. Сейчас многими принята гипотеза Каплана - Йорка, в соответствии с которой размерность аттрактора, называемая ляпуновской, выражается через спектр ЛХП на основе следующих соображений. Пусть известен спектр ЛХП странного аттрактора N-мерной системы. размерность которого нужно оценить:

Пусть числа представляют собой показатели Ляпунова для некоторой динамической системы. Обозначим через j наибольшее целое число, такое, что выполняется неравенство . Тогда, согласно определению, размерность по Ляпунову D_л имеет вид

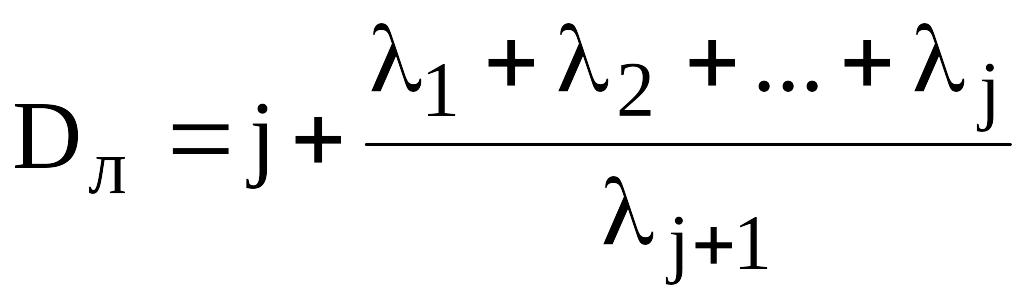(2.40) .

В трехмерной хаотической системе с показателями Ляпунова размерность по Ляпунову определяется в соответствии со следующим простым выражением:

. (2.41)

Для аттрактора выполняется неравенство , откуда следует, что . Для произвольного устойчивого предельного цикла справедливо соотношение , откуда следует, что j=1 и D_л=1. Точно так же размерность двумерного тора по Ляпунову равна D_л=2.

Ляпуновская размерность по определению зависит от типичной траектории x(t), для которой определяется спектр ЛХП, и тем самым автоматически учитывает вероятностные свойства потока. Выражениеполучено из определения размерности , т.е. непосредственным покрытием множества с заданной метрикой, без учета вероятностных свойств различных его элементов. Таким образом, фрактальная и ляпуновская размерности аттрактора совпадают по крайней мере для систем с постоянной степенью сжатия.

Для многомерных динамических систем вопрос о соответствии ляпуновской размерности размерностям натуральной меры и фрактальной пока еще открыт. Однако есть основания полагать, что ляпуновская размерность, как наиболее понятная с физической точки зрения величина, является самостоятельной и важной характеристикой аттрактора. В отличие от фрактальной ляпуновская размерность многомерных аттракторов допускает возможность ее прямого вычисления при больших, но реально допустимых затратах времени на ЭВМ.

В неавтономных системах при периодическом внешнем воздействии выражение можно применить для описания размерности стохастического множества в отображении Пуанкаре через период внешней силы. Для вычисления полной ляпуновской размерности аттракторов неавтономных систем в выражение нужно добавить единицу (или еще один нулевой показатель в спектр ЛХП), тогда

. (2 .42)

Различия в сигнатуре спектров ЛХП и размерность D_л могут быть признаком классификации регулярных и странных аттракторов. Размерность регулярных аттракторов равна числу нулевых показателей в спектре ЛХП. Для регулярных аттракторов в полном соответствии находятся: ляпуновская размерность, фрактальная (метрическая) размерность и сигнатура спектра ЛХП аттрактора. В отношении странных аттракторов о подобном взаимосоответствии можно говорить лишь применительно к трехмерным дифференциальным системам и двумерным отображениям.

Размерность подобных аттракторов D_F = 2 + d, где d << 1, в силу преимущественного сжатия потока в сравнении с растяжением. Такой аттрактор при грубом рассмотрении представляется почти поверхностью с экспоненциально расходящимися по ней близкими траекториями. Поэтому и размерность аттрактора близка к двум. На самом деле таких поверхностей в аттракторе бесконечное множество. Отсюда канторовость структуры в сечении Пуанкаре. Поэтому странные аттракторы не являются многообразиями, а представляют собой прямое произведение многообразия на множество типа канторова.