3.4 Основные формулы комбинаторики

Комбинаторика раздел математики, который изучает количества комбинаций, подчиненных определенным условиям, которые можно со­ставить из элементов, безразлично какой природы, задан­ного конечного множества. При непосредственном вычис­лении вероятностей часто используют формулы комбина­торики. Приведем наиболее употребительные из них.

Перестановками ( ) называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения.

Число всех возмож­ных перестановок:

где n!=1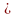 2 3 .. п.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0!==1.

Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

Р3=3!=1 2 3=6.

Размещениями ( 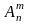)называют комбинации, составленные из n различных элементов по т элементов, которые от­личаются либо составом элементов, либо их порядком.

Число всех возможных размещений:

Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых no 2?

Решение. Искомое число сигналов

Сочетаниями ( 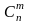) называют комбинации, составленные из « n » различных элементов по « т » элементов, которые отли­чаются хотя бы одним элементом.

Число сочетаний:

Пример 3. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

Замечание. Выше предполагалось, что все n элементов раз­личны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют во другим формулам. Напри­мер, если среди n элементов есть n1 элементов одного вида, n2 эле­ментов другого вида и т. д., то число перестановок с повторениями

При решении задач комбинаторики используют сле­дующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.

1. Понятие суммы и произведения событий.

Перед тем как формулировать и доказывать основные теоремы, введем некоторые вспомогательные понятия, а именно понятия о сумме событий и произведении событий.

Во многих областях точных и экономических наук применяются символические операции над различными объектами, которые получают свои назва­ния по аналогии с арифметическими действиями, рядом свойств кото­рых они обладают. Таковы, например, операции сложения и умно­жения векторов в механике, операции сложения и умножения матриц в алгебре и т. д. Эти операции, подчиненные известным правилам, позволяют не только упростить форму записей, но в ряде случаев существенно облегчают логическое построение научных выводов. Введение таких символических операций над событиями оказывается плодотворным и в теории вероятностей.

Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих вместе.

Например, если событие А — попадание в цель при первом выстреле, событие В — попадание в цель при втором выстреле, то событие С=А+В есть попадание в цель вообще, безразлично при каком выстреле — при первом, при втором или при обоих вместе.

Если события А и В несовместны, то естественно, что появление обоих этих событий вместе отпадает, и сумма событий А и В сводится к появле­нию или события А, или события В. Например, если событие А — появле­ние карты червонной масти при вынимании карты из колоды, событие В—появление карты бубновой масти, то С=А+В есть появление карты красной масти, безразлично—червонной или бубновой.

Короче, суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А и В.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Например, если опыт состоит в пяти выстрелах по мишени и даны события;

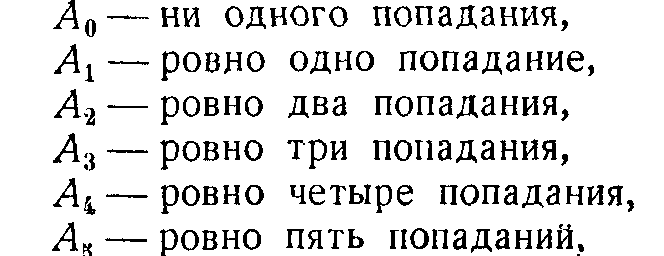
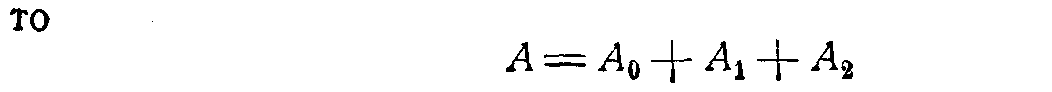
есть событие «не более двух попаданий», а

есть событие «не менее трех попаданий».

На Рис.1.1. наглядно иллюстрированы понятия суммы двух (Рис.1.1 а) и трёх (Рис.1.1 б) событий. Так, если событие А есть попадание точки в область А, соответственно событие В - попадание в область В, то событие А+В есть попадание во все заштрихованные области на Рис.1.1.а. Аналогично на Рис.1.1. б показана сумма для трёх событий.

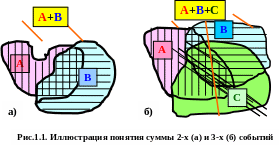
Как видно из представленных рисунков, операция суммы событий аналогична такой логической операции Булевой алгебры, как логическая операция «ИЛИ» (операция дизъюнкции).

Произведением, двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В.

Например, если событие А — появление туза при вынимании карты из колоды, событие В — появление карты бубновой масти, то собы­тие С=АВ есть появление бубнового туза. Если производится два выстрела по мишени и событие А — попадание при первом выстреле, событие В — попадание при втором выстреле, то С = АВ есть попадание при обоих выстрелах.

Произведением нескольких событий, называется событие, состоя­щее в совместном появлении всех этих событий.

Например, если по мишени производится три выстрела и рассма­триваются событияB1 —промах при первом выстреле, В2 — промах при втором выстреле, В3 — промах при третьем выстреле, то событие

состоит в том, что в мишени не будет ни одного попадания.

На Рис.1.2. наглядно иллюстрированы понятия произведения двух (Рис.1.2 а) и трёх (Рис.1.2 б) событий. Так, если событие А есть попадание точки в область А, соответственно событие В - попадание в область В, то событие А В есть попадание в область пересечения обоих областей (области А и области В) на Рис.1.1.а. Аналогично на Рис.1.1. б показана произведение для трёх событий.

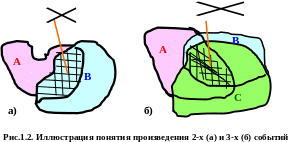
Как видно из представленных рисунков, операция произведения событий аналогична такой логической операции Булевой алгебры, как логическая операция «И» (операция конъюнкции).

При определении вероятностей часто приходится представлять сложные события в виде комбинаций более простых событий, при­меняя и операцию сложения, и операцию умножения событий.

Например, пусть по мишени производится три выстрела и рас­сматриваются следующие элементарные события:

Рассмотрим более сложное событие В, состоящее в том, что в результате данных трех выстрелов будет ровно одно попада­ние в мишень. Событие В можно представить в виде следующей комбинации элементарных событий:

Событие С, состоящее в том, что в мишени будет не менее двух попаданий, может быть представлено в виде:

Такие приемы представления сложных событий часто применяются в теории вероятностей.

Непосредственно из определения суммы и произведения событий следуют 2 важных следствия:

1) А+А+…+А=А

2) А А А …. А=А

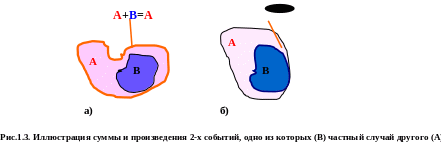
Следует заметить, что если событие В есть частный случай события А, то справедливы следующие два, также важных для практики, выражения, иллюстрация которых приведена также на Рис.1.3:

1) А+В=А;

2) А В= В.